博弈树的搜索

博弈树定义：
一类特殊的与或图
（本次讨论的博弈树都是“与或图”）

应用范围：
下棋、故障诊断、风险投资

基本搜索策略：
极小极大搜索（min-max）

优化的搜索方法：
α-β剪枝搜索
（剪枝）
（搜索与生成同时进行）

了解背景：

（完全博弈问题）博弈问题

特点：
双人对弈：轮流下，一人走一步。
信息完备：双方看到的信息一样
零和：双方利益冲突，对一方有利则对另一方不利。一般对节点N取一个估价函数f(N)，一共两类节点：
——叫Max的极大节点追求最大化，有选择时肯定选值最大的；
——叫Min的极小节点追求最小化，有选择时肯定选值最小的。

例子1：下棋

两位选手对垒，轮流走步。这时每一方不仅知道对方过去已经走过的棋步，而且还能估计出对方未来可能的走步。对弈的结果是一方赢（另一方则输），或者双方和局。如象棋，围棋，五子棋，…

例子2：选包拿钱

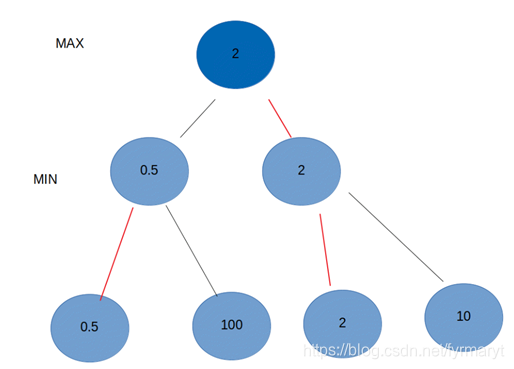
假设有两个钱包，每个钱包都放2张钱，第一个放了0.5元和100元，第二个放了2元和10元， Max和Min两个人是仇敌。现在Max负责挑出一个包，Min负责从Max选的包里选一张小的钱给Max。
因为Max想让自己的钱越多越好而Min不想让Max钱多，所以Min会选一张相对最小的钱给Max。也即，Max想获得最大利益，而Min只是想承受最小的对手变强程度。在这种情况下Max应该选择包2，Min会给他2元。如果Max选择了包1 ，Min只会给他选0.5元。

完全信息博弈抽象出任务原型：
给出（或逐步生成）一个博弈树，求出在指定搜索深度（层数）下的最佳路径和相应估价分数。比如下象棋，Max先走一步，Min再走一步，再轮到Max走，这时Max遇到的各个局面可以估分，再倒推回去Max的第一步应该选择走哪步最佳
基本搜索策略：极小极大搜索（min-max）
为了提高极小极大搜索方法的速度，所以采用剪枝，最主要的是α-β剪枝

不完全信息博弈情况：
大部分纸牌游戏（如斗地主、拖拉机）
大部分即时策略游戏（如红警、星际、帝国）
——需要探路（即信息不对等）
——游戏还受手速（APM）影响

但是博弈问题常常不能简单穷举，以中国相亲为例：
——一盘棋平均走50步，总状态数约为10的161次方。假如一毫微秒走一步，约需10的145次方。
——结论：不可能穷举

极小极大搜索方法：

极小极大搜索方法是博弈树搜索的基本方法。
首先假定，有一个评价函数可以对所有的棋局进行评估。当评价函数值大于0时，表示棋局对我方有利，对对方不利。当评价函数小于0时，表示棋局对我方不利，对对方有利。
方法过程：
1、当轮到我方走棋时，首先按照一定的搜索深度生成出给定深度d以内的所有状态，计算所有叶节点的评价函数值。然后从d-1层节点开始逆向计算：
2、对于我方要走的节点（用MAX标记，称为极大节点）取其子节点中的最大值为该节点的值（因为我方总是选择对我方有利的棋）。
3、对于对方要走的节点（用MIN标记，称为极小节点）取其子节点中的最小值为该节点的值（对方总是选择对我方不利的棋）。
4、一直到计算出根节点的值为止。获得根节点取值的那一分枝，即为所选择的最佳走步。
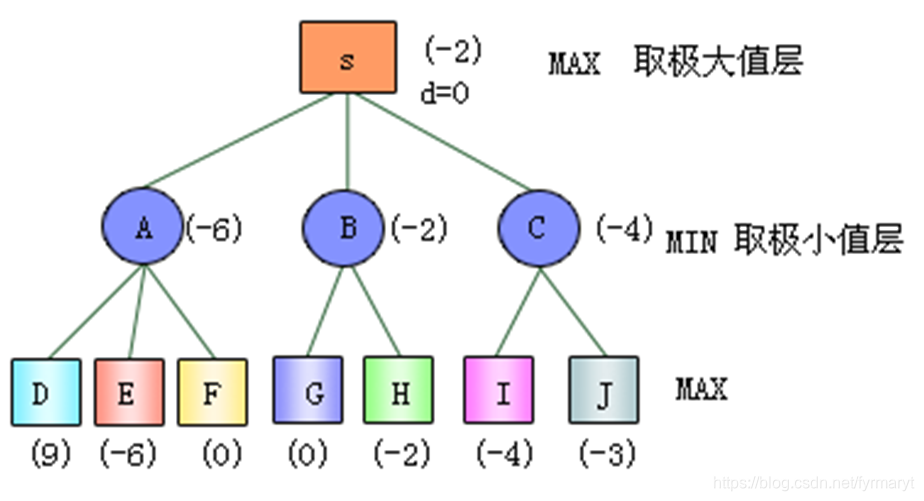
图2 极小极大搜索
因此，极小极大过程是一种假定对手每次回应都正确的情况下，如何从中找出对我方最有利的走步的搜索方法。
值得注意的是，不管设定的搜索深度是多少层，经过一次搜索以后，只决定了我方一步棋的走法。等到对方回应一步棋之后，需要在新的棋局下重新进行搜索，来决定下一步棋如何走。

对于静态估计函数f(x)
一般规定有利于MAX的势态，f§取正值，有利于MIN的势态，f§取负值，势均力敌的势态，f§取0值。若f§＝＋∞，则表示MAX赢，若f§＝－∞，则表示MIN赢。下面的讨论规定：顶节点深度d＝0，MAX代表程序方，MIN代表对手方，MAX先走。
当用端节点的静态估计函数f（p）求倒推值时，两位选手应采取不同的策略，从下往上逐层交替使用极小和极大的选值方法，故称极小极大过程。

个人总结：
极小极大搜索——从一个原始状态节点，根据估值函数，对后面出现的可能状态进行估值，在一定深度内通过一个路径选择方式（max层节点从子节点选择最大的值，min层节点从子节点总选择最小的值），选择出最优的路径（该路径为到达最优值所在节点路径）。

α-β剪枝搜索过程：

能否在搜索深度不变的情况下，利用已有的搜索信息减少生成的节点数呢？
MIN-MAX过程是把搜索树的生成和格局估值这两个过程分开来进行，即先生成全部搜索树，然后再进行端节点静态估值和倒推值计算，这显然会导致低效率。
实际上把生成和倒推估值结合起来进行，再根据一定的条件判定，有可能尽早修剪掉一些无用的分枝，同样可获得类似的效果，这就是α-β过程的基本思想。

注意： α-β剪枝搜索和生成扩展子节点是同步的。其得到的最优解结果与Min-Max过程一致
Min-Max过程和α-β剪枝搜索的结果都受生成/搜索策略顺序有关（比如选择广度优先或者深度优先，结果可能不一样）

简单例子：

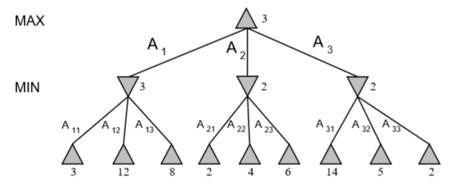
图3 极小极大搜索方法
由图3可知，对于min-max搜索，得到的最优路径为A1-A11。max得分为3

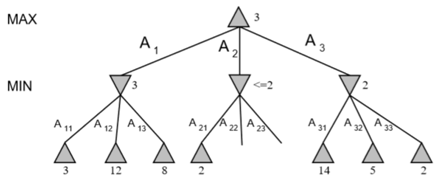
图4 α-β剪枝方法
而图4是通过α-β剪枝方法得到的，同样得到最优路径为A1-A11。max得分为3。

例子2：

对该搜索树进行左边深度优先α-β剪枝搜索

图5 例子2
左边为原搜索树，右边为α-β剪枝搜索
——极小值节点I的N子树被剪枝了（ α剪枝）
——极大值节点G的L子树被剪枝了（β剪枝）

α-β搜索方法定义：
Max节点的下界为α，即Max确保能获得的最小得益。初始化为-inf。
Min节点的上界为β，即Min付出的上界代价保障。初始化为+inf。
对于节点N的估计函数值f(N)，初始化α =-inf ≤ f(N) ≤ β=+inf
若 α ≤ β则N有解。若 α > β 则N无解(为什么无解？因为对于上一层，min/max层不会选择该路径的节点了，故而可以放弃搜索)，该节点N的其他未访问子树会被剪枝
如图中节点I，从左子树DBE可以获得下界α=3，并传送到右边的极小节点I，此时I的子节点M给了个上界β=1。所以α=3> β=1，下界α大于上界β ，无解。

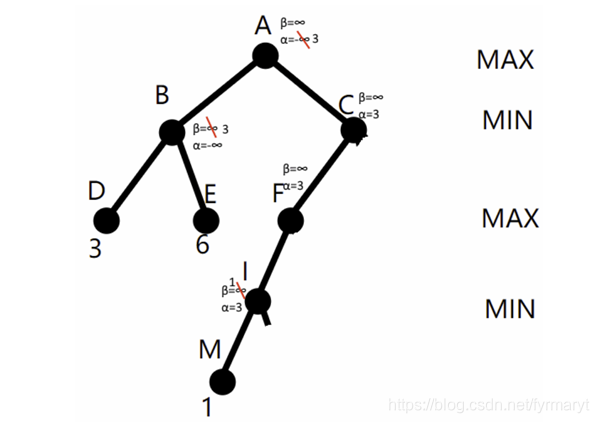
在这里插入图片描述
理解：
极大节点N，从一个子树获得的α值和β值，可以传送给其子节点
极大节点N 的α值只可能越改越大，否则极大节点N可以还选择原有α值
极小节点M的β值只可能越改越小，否则极小节点M可以还选择原有β值
从单边子节点往父节点推，极大值父节点只更改α值，极小值父节点只更改β值。

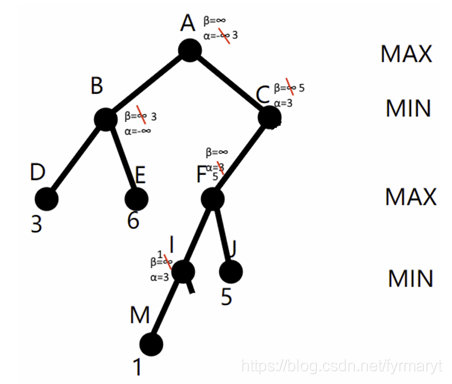
在这里插入图片描述
α剪枝（发生在极小层节点，如图中的节点I）
（1）α剪枝：若任一极小值层节点的β值小于或等于它任一先辈极大值层节点的α值，即α（先辈层）≥β（后继层），则可中止该极小值层中这个MIN节点以下的搜索过程。这个MIN节点最终的倒推值就确定为这个β值。
从一个子树获得的极大节点的α值，可以传送给该节点的其他子树，从而选择α剪枝机会（课本说法，和“先辈”节点α值比较，是和所有先辈节点比较，而不是仅仅和父节点比较）。
从单边子节点往父节点推，极大值父节点只更改α值，极小值父节点只更改β值

注意看极小节点I：
极大节点A从左子树获得α值3，从而可以把α=3传播给右子树，在极小节点I点由于子节点M值为1从而可以确认β=1，此时α=3> β=1，从而I的其他节点可以被α剪枝, I点的β=1。

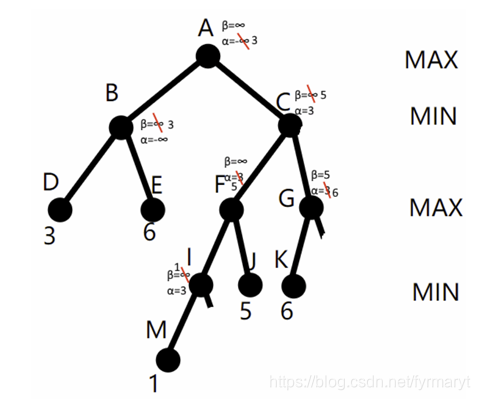
在这里插入图片描述
β剪枝（发生在极大层节点，如图中的节点G）
（2）β剪枝：若任一极大值层节点的α值大于或等于它任一先辈极小值层节点的β值，即α（后继层）≥β（先辈层），则可以中止该极大值层中这个MAX节点以下的搜索过程。这个MAX节点的最终倒推值就确定为这个α值。
从一个子树获得的极小节点的β值，可以传送给该节点的其他子节点，从而选择β剪枝机会（课本说法，和“先辈”节点β值比较，是和所有先辈节点比较，而不是仅仅和父节点比较）。
从单边子节点往父节点推，极大值父节点只更改α值，极小值父节点只更改β值