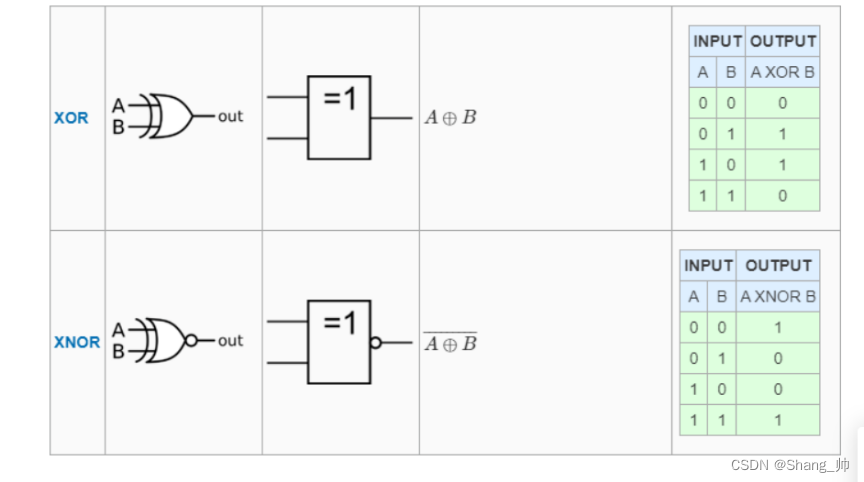
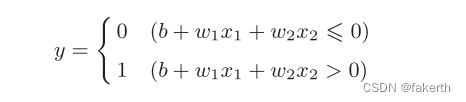黎曼积分是逐项可积的，对于逐项不可积的函数黎曼积分无能为力，需要Lebsgue积分。本篇先从最基本的导数开始，然后到微分，最后到黎曼积分，下一篇讲述Lebsgue积分和实变函数的积分，后面再讲度量空间，泛函数与线性算子，最后到希尔伯特空间的几何算子。另外还增加《凸优化》的部分。

本篇文章重点关注的是数学思想，而不是现有结论的重复论述。数学证明最能反映一个人的数学思维，而不是解题。当年牛顿被苹果砸脑袋发现了万有引力。发现过程中国的课本从来没有详细论述过，就告诉学生这么一个现象，等于没说！如果没有之前微积分的创立，再多的苹果砸在脑袋上，也不会发现万有引力。数学应用也很关键，比如傅立叶变换在nlp中的应用：应用在无向图推理中，拉普拉斯矩阵的特征分解。应试教育培养出来的人思维僵化，注重解题，思维不开阔。对于一项结论，我们必须知道是如何来的，这个过程远远高于解题。数学和物理是一家，有很多数学公式的推导，都是从物理学中得到启发的，包括AI。上传本人的草稿：

 

 

 

最后部分：应用与拓展

1.微积分的本质：微分是因，积分是果。没有微分就没有积分，微分的核心思想是在微观领域，运用无限微元分割的手段达到极限时以直代曲。具体地，设有一点x，在x的不远处有一点y，运用极限思维，让y无限逼近x直到y是x附近的一点，此时满足以下两个关系：图在后面

 第一个是一阶条件，第二个是x的梯度可以近似地用附近点的一阶差分来代替。更具体一些，用信号来解释，设在一段时间内输入信号x，把每个时间点看成自变量，信号是因变量。衡量输入信号x的变化率时，首先将信号输入时序分割，每段的变化率也就是微元x的梯度，用每段信号的差分与微分的比值来代替求解梯度。当x是向量时，y-x有特定的含义：它表示参数的搜索方向，亦代表方向向量，那么梯度和y-x的内积则代表方向导数。一阶条件在很多方面有着重要的应用。在《凸优化》的参数优化算法中，比如回溯直线搜索算法的收敛条件分析，主要考虑当参数趋近到最优解附近时的一阶条件，再比下面的例子，很好地阐释了微积分的本质：如何运用极限思维，离散化积分

一阶差分，二阶差分在凸优化的结构化约束中经常用到，比如控制参数的稳定性，让信号输入变化平稳一些。

2.拓展

由积分的离散化我们可以得到更多的启发：既然函数与坐标轴围成的面积是众多小矩形面积之和，那么我们可以得到这样一个结论：如果随机变量x是均匀分布的，f(x)的面积可以用一个大矩形近似。这个矩形的高是众多小矩形高的期望。设x取值范围为a～b，那么它的概率密度函数为1/（b-a）。图形的面积就是。注意这是用概率来解决问题了，这里的高是根据累积经验分布函数的单点概率为1/n得出的。如何模拟这个期望呢？比如如何求出下面图形的面积？

这个图形的函数公式是几乎不可能求出的。运用前面的思考，我们可以把它装在一个矩形里面，让图形与矩形刚好接触。然后我们往矩形框里随机地撒点，当数量达到一定量级后，计算落在蝙蝠里面的点，再除以总点数，得出概率值。用这个概率值乘以矩形对面积就可近似算出蝙蝠的面积。

前面提到的是均匀分布，如果随机变量是其他分布呢？设随机变量的概率密度函数为q(x)，则有。把后面的离散化了，我们可以知道，这个公式相当于从分布q(x)中抽取样本f(x)/q(x)。

3.高斯积分

这部分的内容进一步强化积分，二重积分的意义是求体积，离散化是微元面积与高的乘积之和。微元面积在笛卡尔坐标系中就是小矩形的面积，但是对于e^-x^2函数是无法求出积分的。必须转换为极坐标才能求出微元面积，进而求出积分。下面的草稿很潦草，凑合着看吧：

4.幂级数分解与三角级数分解

世界上没有绝对的直线，也没有绝对的平行线，但是在宏观领域是成立的。一个矩形信号是由无数个曲线波形叠加而成的。从代数和几何统一的角度来看，指数函数可以看作是一个无限维度的向量，一个点，它的基有无数个。它的坐标可以分解为级数与基（矩阵）的乘积。函数的级数分解，一阶近似就是前面的微分。关于这部分，可以查看本人关于傅立叶变换的博客。

正确深入理解微积分，光学习一两本通用本科的数学是远远不够的。高等数学尤其是现代数学，领略思想精髓然后解决实际问题是关键，这点明显不同于高中数学。应用数学领域，首先要强化建模能力，其次是参数求解能力。后者涉及到算法优化，和计算机直接相关。