转自:https://www.zhihu.com/question/36959297/answer/83465328
作者:知乎用户
链接:https://www.zhihu.com/question/36959297/answer/83465328
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
这里用些不太准确的描述来了解黎曼几何,只是用来理解的。
------------------------
先啰嗦几句历史。
黎曼空间(Riemannian Spaces)就是黎曼几何(Riemannian Geometry)能够成立的空间。
黎曼几何是由德国数学家G. F. B. Riemann黎曼在19世纪中期提出的几何学理论。
黎曼几何中的一个基本问题是它的微分问题。该问题大约在1869年前后由E.B.Christoffel(注意这个英文名字,后面要用好多次)和李普希茨等人解决。前者的解包含了以他的姓命名的两类Christoffel符号和协变微分概念。
- 一句话总结,基矢量的导数是Christoffel符号,张量的梯度就是协变导数
在此基础上G.Ricci发展了张量分析方法,这在广义相对论中起了基本数学工具的作用。E.嘉当在20世纪20年代开创并发展了活动标架法,建立了李群与黎曼几何之间的联系,从而为黎曼几何的发展奠定重要基础。(Christoffel符号就是群量)
1915年,爱因斯坦运用黎曼几何和张量分析工具创立了新的引力理论——广义相对论。
大致就是这个路子。
------------------------
什么是黎曼几何?
先说个名词:空间(Space)。下面的叙述中,一定要正确理解它。比如,线空间,这里的意思就是线,点绝对不会离开这条线,这里“空间”就是这条线,而不是日常中提到的神马XX空间。进一步说下,在A4纸上画个线,如果提了线空间,也不要让脑子以为空间是那个A4纸。一定记住哦!又比如,面空间,那么就是面本身,上面的点和线绝对不会离开这个面。比如A4纸是个面空间,那么,即便你把纸卷一下,上面的任何点线也都不能离开这个纸面。Ok了,后面迷糊了就再到这里看一下这个词。
好了,黎曼空间就是弯曲的空间。比如,弯曲的线空间,弯曲的面空间。
这是定义。
黎曼的重大作用就在于,改变了认识,就是思考的角度不同了。
比如,在A4上画了一个曲线。
一般的认识(欧氏里的认识)就是,在面空间上有了一个对象(就是线)。【欧氏空间,不是欧拉创立的哈,是欧几里德,Euclidean Spaces】
但是在黎曼看来,是在线空间上有了一个对象(还是那条线)。
看到不同了吗?
在欧氏几何里,要用二维或者三维空间,才能描述这条线。
在黎曼几何里,用一维空间就可以!(即便是欧氏三维空间里的一条曲线)
星星还是那个星星,但是,一切又都不一样了。虽然现在一切都还不明朗,但是大门已经开了一条缝隙。
这就是思考的力量!
对比着来理解。平常用的多是欧氏几何(Euclidean Geometry)。在欧氏空间里,笛卡尔坐标系是个标志性建筑,实际上,也是判断欧氏几何的标准:必须能用笛卡尔系表示的,才能是欧氏几何。
对于Euclidean空间,必定存在一个适用于全空间的笛卡尔坐标系,所以Euclidean空间也称为笛卡尔空间,其他坐标系和笛卡尔坐标系满足一一对应的坐标转换关系。
书面话读起来总是很累....
比如。。。
先说一个名词,基标矢量。
在笛卡尔系里,我们一般默认了尺规是单位1,一般也不标注。这里我们把它带上单位,这个单位带上方向就是基标矢量。
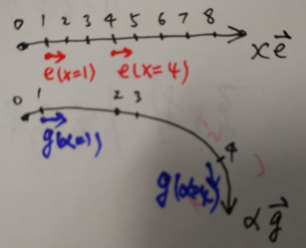
接着说...
在第一条黑色的线里(欧氏线空间里的线),各个间隔相同,而且,基标矢量e(它是矢量哟)的方向也一致。基标矢量连成的线是直的(红色的),也就是说,基标矢量的斜率是0,就是说基标矢量的导数是0(导数、斜率和梯度一个意思,这里),也就是说,它!不!!弯!!!
再看下面的黑线(黎曼线空间里的线),每个号码之间的间隔不同,而且,基标矢量g的方向也在一直变(看蓝色),也就是说,这个线空间是弯曲的!而且,这个基标矢量的大小不一定是1哟。
So来总结一下,基标矢量的空间变化率是零就是欧氏空间,大于零就是黎曼空间。
所以,黎曼空间本质上就是弯!曲!的!
基标矢量的空间变化率其实就是那个Christoffel符号(回头再开一贴说它)。
又比如
在黎曼空间里,坐标线不一定是直的,坐标线的尺规可以不是单位1(可以每个地方都不同),坐标线之间也不一定是垂直的。
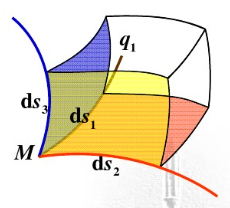
黎曼几何可以看做是欧式几何的推广,或者说,欧氏几何是黎曼几何的特例(欧氏几何是弯曲为零的黎曼几何)。
在公式上,区别这两类空间,依靠的是...当当当当.... Riemann-Chiristoffel Tensor,用R表示。R是一堆Christoffel符号的组合,神烦。
R=0就是欧氏空间,R>0就是黎曼空间。
-------------------------
继续搬点文字(就是抄来的,嘿嘿…..)
欧氏几何认为人生活在一个绝对平的世界里,因此在平面里画出的三角形三条边都是直的。两点之间的距离也是直的。但是假如生活的空间是一个曲面,这个曲面,可以把它想象成一口平滑的锅或太阳罩。然后就在这个曲面里画三角形,这个三角形的三边的任何点都绝对不能离开曲面。我们将发现这个三角形的三边无论怎么画都不会是直线,经过论证发现,任何这种三角形的内角和都永远小于180度,无论怎么画都不能超出180度,但是当把这个曲面渐渐展开,一直舒展成绝对平的面,这时三角形就变成了欧氏三角形,也就是在初中学的平面几何,其内角和自然是180度。
在平面上,两点间的最短距离是线段,但是在曲面上,两点间的最短距离则是曲线,因为平面上的最短距离在平面上,那么曲面上的最短距离也只能在曲面上,而不能跑到曲面外抻直,故这个最短距离只能是曲线(最近有个电影很火的,星际穿越,里面就解释了这个,去看看吧)。若我们把双曲面舒展成平面以后,再继续朝平面的另一个方向变,则变成了椭圆面或圆面,这个时候,如果我们在这个椭圆面上画三角形,将发现,无论怎么画,这个三角形的内角和都大于180度,两点间的最短距离依然是曲线,这个几何就是黎曼几何。这个几何在物理上非常有用,因为光在空间上就是沿着曲线跑的,并非是直线,我们生活在地球上,因此我们的空间也是曲面,而不是平面,但为了生活方便,都不做严格规定,都近似地当成了平面。
--------------------------------
再多唠叨两句,灰常担心这几句会把上面的理解又搞混了。
是不是说欧氏空间不能用曲面呢?
否
有个等距变换的概念在里面。
例如,平面是二维的Euclidean空间,如果将平面进行弯曲,这个过程中保持面上的线段长度都不变,于是平面能变成圆柱面等,这个就是等距变换。在等距变换后的面上,Euclidean几何学仍然适用,所以这个圆柱面也是Euclidean空间。
一个不同的例子,是球面。在球面上,Euclidean几何学是不适用的,而且平面也无法通过等距变换变为球面。