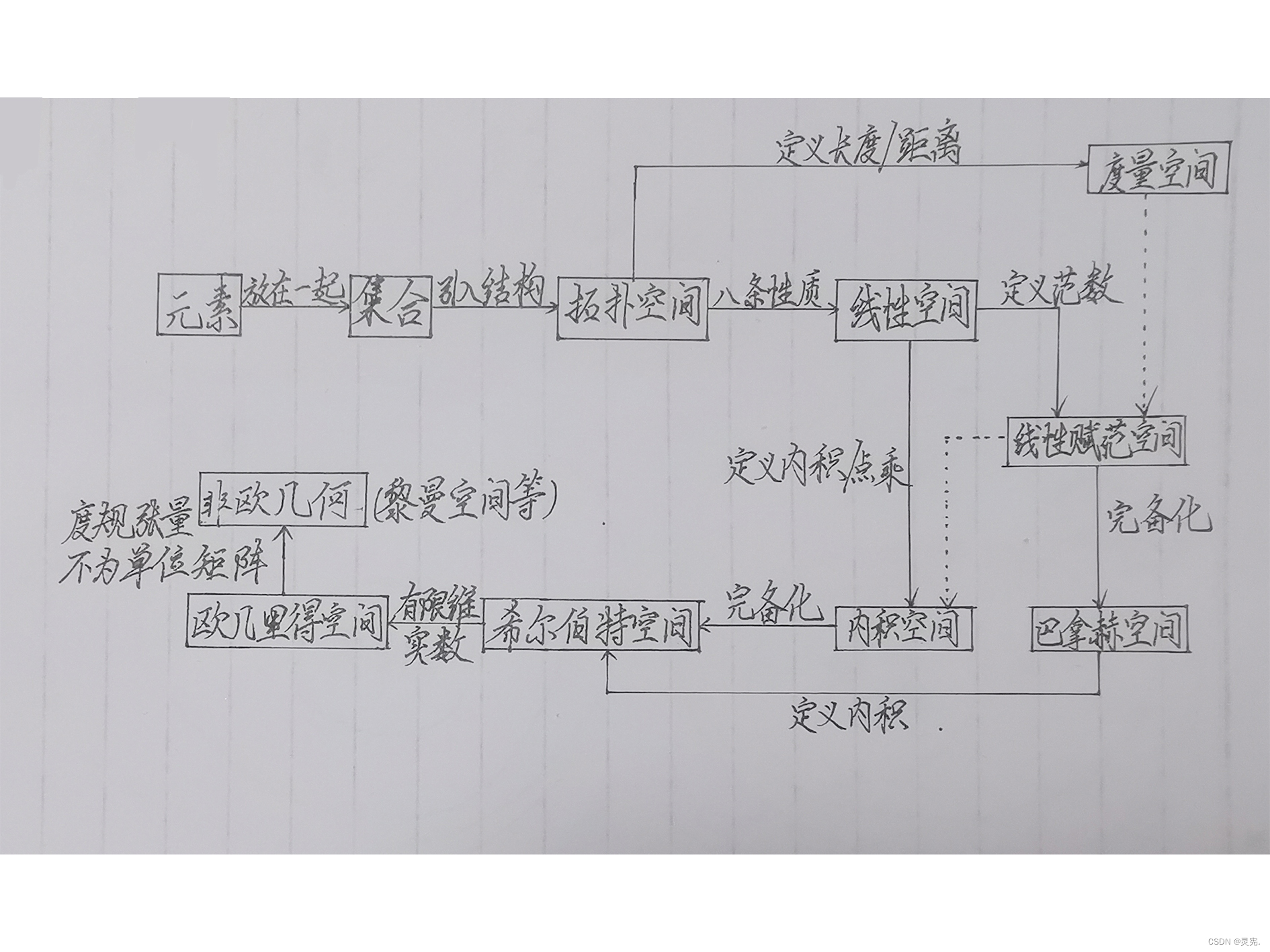
欧式空间与希尔伯特空间

一.欧式空间（欧几里得空间）

百度百科中关于欧式空间的定义：

设V是实数域R上的线性空间(或称为向量空间)，若V上定义着正定对称双线性型g(g称为内积)，则V称为(对于g的)内积空间或欧几里得空间(有时仅当V是有限维时，才称为欧几里得空间)。（很懵！）具体来说，g是V上的二元实值函数，满足如下关系：

(1) g(x,y) = g(y,x)

(2) g(x+y,z) = g(x,z) + g(y, z)

(3) g(kx,y) = kg(x,y) 

(4) g(x,y) >= 0,而且g(x,y)=0当且仅当x=0时成立。

这里x,y,z是V中任意向量,k是任意实数。

例子：

1. （经典欧几里德空间E^n）在n维实向量空间R^n中定义内积(x,y)=x1y1+...+xnyn，则Rn为欧几里德空间。（事实上，任意一个n维欧几里德空间V等距同构于E^n。）

2. 设V是[0,1]区间上连续实函数全体，则V是R上线性空间，对于如下内积是欧几里德空间：(f,g)定义为fg在[0,1]区间上的积分值。

标准欧几里得空间

四维空间被称为标准欧几里得空间，可以拓展到n维；四维时空指的是闵可夫斯基空间概念的一种误解。人类作为三维物体可以理解四维时空(三个空间维度和一个时间维度)但无法认识以及存在于四维空间，因为人类属于第三个空间维度生物。通常说时间是第四维即四维时空下的时间维度。四维空间的第四维指与x,y,z同一性质的空间维度。然而四维时空并不是标准欧几里得空间，时间的本质是描述运动的快慢。

通过一维，二维，三维空间的演变，人们提出了关于四维空间的一些猜想。尽管这些猜想现在并不能证明是正确的，但科学理论有很多是猜想开始的。现今科学理论一般是基于现象总结规律，而关于四维空间的现象没有足够准确清晰的认识，或者看到了这种现象却并没有想到是四维空间引起的。

 

二.希尔伯特空间

百度百科中希尔伯特空间：

在数学中，希尔伯特空间是欧几里得空间的一个推广，其不再局限于有限维的情形。与欧几里得空间相仿，希尔伯特空间也是一个内积空间，其上有距离和角的概念(及由此引申而来的正交性与垂直性的概念)。此外，希尔伯特空间还是一个完备的空间，骑上所有的柯西序列等价于收敛序列，从而微积分中的大部分概念都可以无障碍的推广到希尔伯特空间中。希尔伯特空间为基于任意正交系上的多项式表示的傅里叶级数和傅里叶变换提供了一种有效的表述方式，而这也是泛函分析的核心概念之一。希尔伯特精简是公式化数学和量子力学的关键性概念之一。

 

希尔伯特空间是欧几里德空间的直接推广。对希尔伯特空间及作用在希尔伯特空间上的算子的研究是泛函分析的重要组成部分。

设H是一个实的线性空间，如果对H中的任何两个向量x和y，都对应着一个实数，记为(x，y)、满足下列条件：

①对H中的任何两个向量x，y，有(x，y)=(y，x);

②对H中的任何三个向量x、y、z及实数α、β，有(αx+βy，z)=α(x，z)+β(y，z);

③对H中的一切向量x，均有(x，x)≥0，且(x，x)=0的充分必要条件是x=0。则(x，y)称为是H上的一个内积，而H称为内积空间。

如果定义

  

，则在‖0‖下，H构成一个线性赋范空间。

完备的内积空间称为希尔伯特空间，希尔伯特空间的概念还可以推广到复线性空间上。

欧几里德空间是希尔伯特空间的一个重要特例，希尔伯特空间的另一个最重要的特例是L(G)，设G是n维欧几里德空间中的一个有界闭域， 定义在G上的满足⨜G|f(x)|dx<+∞的勒具格可测函数全体记为L(G)，在L2(G)中引入内积(f，g)=⨜Gf (x)g(x)dx，则L(G) 是一个希尔伯特空间，L(G)是实用中最重要和最常用的希尔伯特空间。

希尔伯特空间有许多与欧几里德空间相似的性质，例如，在希尔伯特空间中，可以定义向量正交、正交和、正交投影的概念，柯西一许瓦兹不等式成立、勾股定理和投影定理成立。在可分希尔伯特空间中，存在着完全的标准正交系，希尔伯特空间中的任一向量可以依任一完全的标准正交系分解。

在泛函分析中，详细地研究了希尔伯特空间自共轭算子的理论，特别是自共轭算子的谱理论，这一理论在经典数学的不少领域中有广泛的应用。需要特别指出的是，自共轭算子的谱理论，为量子力学的发展，提供了适合的工具。

理论数学、应用数学和物理中的许多问题，在希尔伯特空间中，可得到较好的处理，因此，希尔伯特空间成为泛函分析中最重要的和最常用的一类空间，它在许多其他数学分支、理论物理和现代工程技术理论中，也得到了广泛的应用。 [2] 

 

本文参考

1.维基百科 欧几里得空间https://zh.wikipedia.org/wiki/%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E7%A9%BA%E9%97%B4

2.百度百科

https://baike.baidu.com/item/%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%B7%E7%A9%BA%E9%97%B4/8281167?fr=aladdin

https://baike.baidu.com/item/%E5%B8%8C%E5%B0%94%E4%BC%AF%E7%89%B9%E7%A9%BA%E9%97%B4

3.参考CSDN博客

https://blog.csdn.net/u014697805/article/details/78292413