微信关注:脑机接口研习社
追踪脑机接口发展最新资讯
系列文章目录
脑机接口专栏 | 利用黎曼几何分析EEG脑电信号(一)
脑机接口专栏 | 利用黎曼几何分析EEG脑电信号(二)
文章目录
- 系列文章目录
- 前言
- 一、对拓扑的定性理解
- 二、集论初步
前言
在粉丝们的催促下,小编加班加点地学习,终于更新了黎曼几何分析EEG脑电信号的专栏文章!
此专栏将在未来的数月时间中进行不定时更新,敬请期待。
为保内容精准详实,本文主要是对**梁灿彬老师的《微分几何入门与广义相对论》**的注解,配合网络上的其它资料,以及小编自己的理解。如有侵权或不明之处,可留言。
一、对拓扑的定性理解
拓扑被称为是“橡皮膜上的几何学”,在二维实数空间中,正方形和三角形的拓扑是一样的。
所谓“拓扑”就是把实体抽象成与其大小、形状无关的“点”,而把连接实体的线路抽象成“线”,进而以图的形式来表示这些点与线之间关系的方法,其目的在于研究这些点、线之间的相连关系。表示点和线之间关系的图被称为拓扑结构。拓扑结构与几何结构属于两个不同的数学概念。在几何结构中,我们要考察的是点、线之间的位置关系,或者说几何结构强调的是点与线所构成的形状及大小。如梯形、正方形、平行四边形及圆都属于不同的几何结构,但从拓扑结构的角度去看,由于点、线间的连接关系相同,从而具有相同的拓扑结构即环型结构。也就是说,不同的几何结构可能具有相同的拓扑结构。
参考:https://www.zhihu.com/question/26507158/answer/409420878
更加形象化的解释是:
如果所有图形都是用橡皮做成的,我们就能将许多图形进行拓扑变换。例如一个圆圈,可以变成一个方圈、一个三角圈。但是一个圆圈不能由拓扑变换成为一个阿拉伯数字“8”。因为不把圈上的两个点重合在一起,圈就不会变成8。
参考:https://www.zhihu.com/question/26507158/answer/1605167125
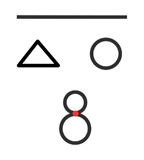
上面的回答有几个重点:
- 拓扑是一种抽象概念;
- 拓扑是找到实体之间的共性;
- 拓扑结构与几何结构是不同的,
- “拓扑结构”是一个与“拓扑”不一样的概念.该回答还有一个误区,就是总把拓扑与几何联系在一起。
在梁老师的书里,拓扑是由集合引出的,而非几何,几何中的线、点、面,实际上是你的“原空间”经过map(映射)后在“像空间”的像点。
拓扑与几何不是等价关系。
那么研究拓扑的拓扑学是什么学科呢?
拓扑学(英语:topology),或意译为位相几何学,是一门研究拓扑空间的学科,主要研究空间内,在连续变化(如拉伸或弯曲,但不包括撕开或黏合)下维持不变的性质。在拓扑学里,重要的拓扑性质包括连通性与紧致性。
参考:https://zh.wikipedia.org/wiki/%E6%8B%93%E6%89%91%E5%AD%A6
拓扑学可以分为:
一般拓扑学建立拓扑的基础,并研究拓扑空间的性质,以及与拓扑空间相关的概念。一般拓扑学亦被称为点集拓扑学,被用于其他数学领域(如紧致性与连通性等主题)之中。
代数拓扑学运用同调与同伦群等代数结构量测连通性的程度。
微分拓扑学研究在微分流形上的可微函数,与微分几何密切相关,并一起组成微分流形的几何理论。
几何拓扑学主要研究流形与其对其他流形的嵌入。几何拓扑学中一个特别活跃的领域为“低维拓扑学”,研究四维以下的流形。几何拓扑学亦包括“纽结理论”,研究数学上的纽结。
为什么拓扑学这么学科会存在呢?
说说个人感悟:
拓扑学其实就是研究分析学搞出来的。请回想你初次学习数学分析时接触的是实直线连续统,在那里花了不少精力研究。因为那时函数的定义域是取自实直线的,为了确保分析的基础,必须花精力研究实直线。后来要对分析学进行推广(请注意数学研究中必做的事情,对现有理论进行完善推广),就提出如果函数的定义域不是实直线,比如复数,其他的空间,我们现有的理论还适用吗?对于这个问题我们显然没有底气说一定适用!因为函数的定义域是我们没见过的,不熟悉的。基于此,我们就得系统的对它们进行研究,但我们又不可能对每一个都去研究,就抽象成一个普遍适用的来进行研究,即公理化!所以你会见到后来学过的序关系,这个是为了给任意空间中的集合定义有界用的,引入拓扑空间是为了定义开闭集(以前实直线上开闭区间的推广),有了这两样就可以推广以前的有界闭区间为紧集,然后再对分析学的三大基本定理(极值、介值、一致连续)以紧集进行推广论证,还有其他的各种推广,这样我们就逐步建立了另一种抽象的,观点更高的分析。
参考:https://www.zhihu.com/question/30743984/answer/82039418
连续统的概念:
连续统(Continuum)是一个数学概念。当人们笼统地说:“在实数集里实数可以连续变动”,也就可以说实数集是个连续统;更严格的描述需要使用序理论、拓扑学等数学工具。这里的连续是相对于离散的概念而言的。在不讨论精确的定义前,有时人们也会谈到一个量可以在某范围内连续取值,或者说该量的变化范围是一个连续统。在数学上,连续统这一术语至少有两种精确定义,但并不等价。另外,连续统一词有时即指实数线或者实数集,这是较旧的叫法。
参考:https://zh.wikipedia.org/wiki/%E8%BF%9E%E7%BB%AD%E7%BB%9F
我们从点集拓扑学入手理解拓扑与拓扑空间。
我们以梁灿彬老师的书为蓝本,一句一句的理解。
二、集论初步

重点:全体实数集合R与空集Ø
 重点:空集是任意集合的子集
重点:空集是任意集合的子集

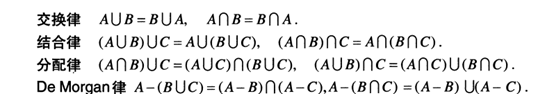
重点:注意这些定律的对偶关系。比如demorgan律,前一条是后一条的对偶律。德摩根定律在数理逻辑的定理推演中,在计算机的逻辑设计中以及数学的集合运算中都起着重要的作用处。下证demorgan律。

注释:上述证明采用了“从特殊性看问题”的方法。这里推荐一本苏淳老师的小册子,《从特殊性看问题》,对培养思维很有好处。

举个例子,集合a={1,2,3},b={A,B,C},则axb={(1,A),(1,B),(1,C),(2,A),(2,B),(2,C),(3,A),(3,B),(3,C)}。

重点:R^n 这个概念非常重要。我们所在的四位空间可以理解为R^4。自然坐标这个概念也要理解。从自然坐标可以引出距离和映射的概念,我们下期见。
未完待续……
参考资料:
《微分几何入门与广义相对论》 第二版 梁灿彬 周彬 科学出版社