单调栈及单调栈的应用

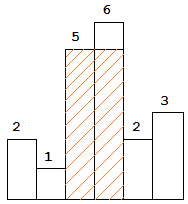
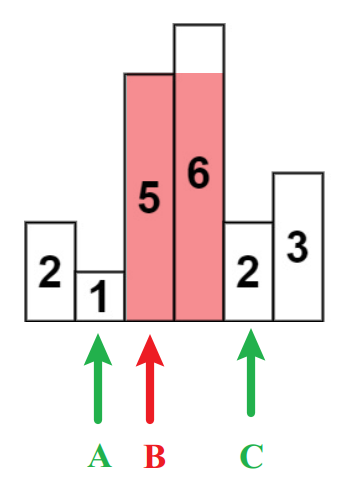
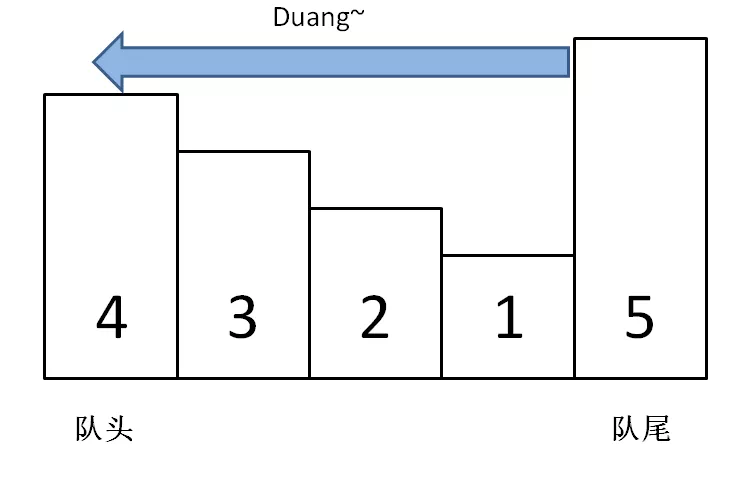
什么是单调栈

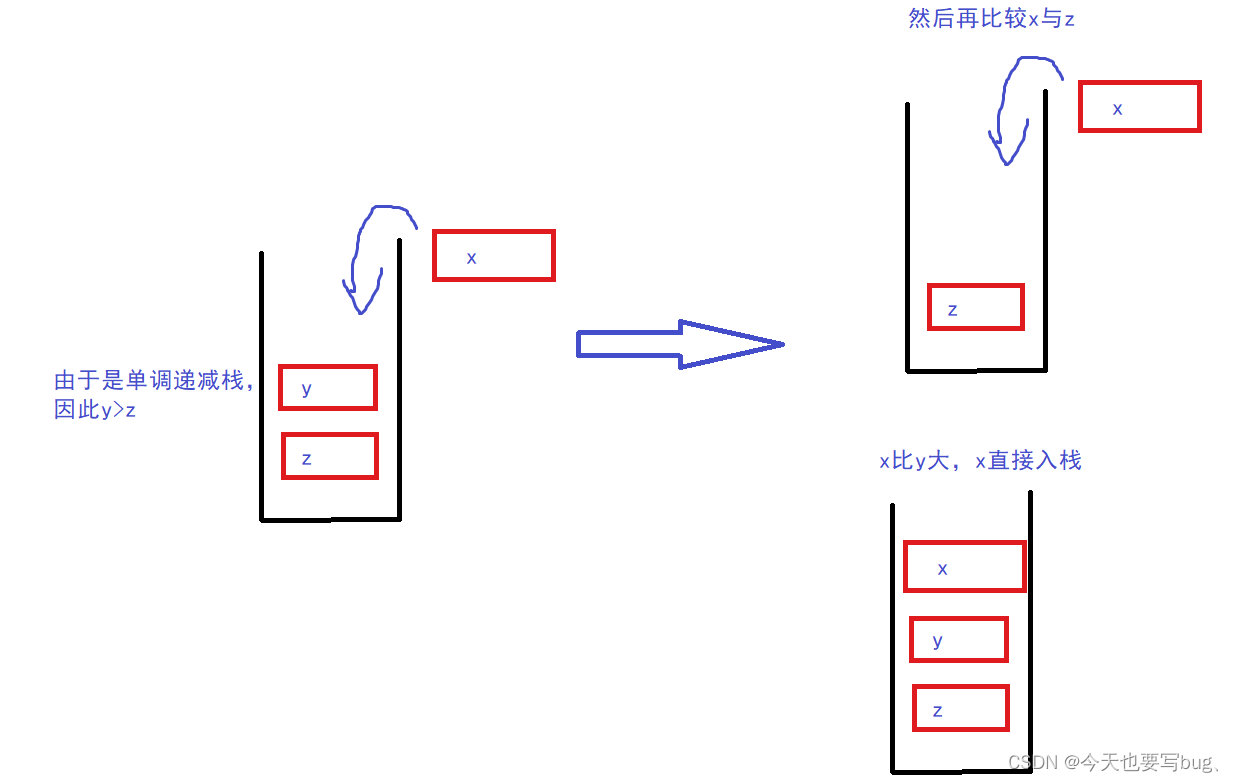
单调递增栈：单调递增栈就是从栈底到栈顶数据是从大到小
单调递减栈：单调递减栈就是从栈底到栈顶数据是从小到大

解决那类问题

要知道单调栈的适用于解决什么样的问题，我们首先需要知道单调栈的作用。单调栈分为单调递增栈和单调递减栈，通过使用单调栈我们可以访问到下一个比他大（小）的元素（或者说可以）。也就是说在队列或数组中，我们需要通过比较前后元素的大小关系来解决问题时我们通常使用单调栈。下面我们通过简单介绍单调减栈和单调增栈问题来进一步说明使用单调栈处理问题的过程。

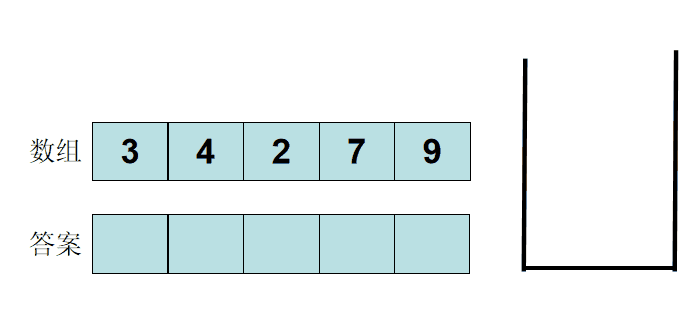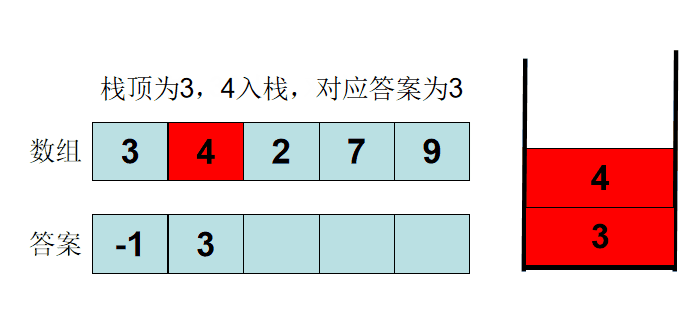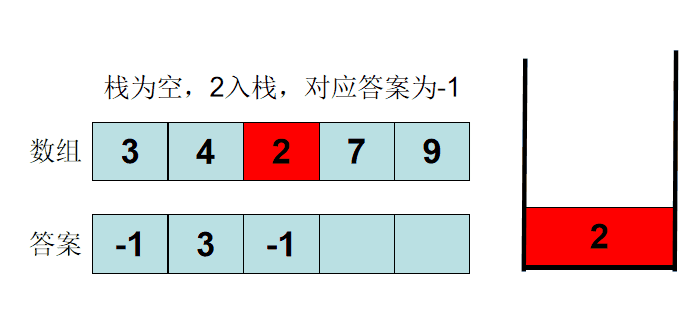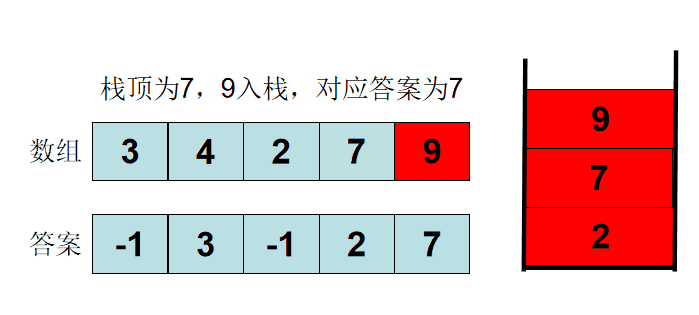
模拟实现一个递增单调栈：

做一个从栈顶到栈底递减的单调栈，当栈为空或者是栈顶元素小于入栈元素时入栈，当栈不为空同时栈顶元素大于入栈元素时，pop栈顶元素，直到遇到入栈元素大于栈顶元素时，最后一次出栈的元素就是左端第一个比它小的数

10，3，7，4，12

10入栈时，栈为空，直接入栈，栈：10

3入栈时， 3<10 ，10出栈，此时栈为空，3入栈，栈：3

7入栈时，7>3，7入栈，栈：3，7

4 入栈时，7>4,7出栈，3<4，4入栈，栈：3，4

12 入栈时， 12>4 ，入栈，栈；3，4，12

伪代码

stack<int> st;
//此处一般需要给数组最后添加结束标志符，具体下面例题会有详细讲解
for (遍历这个数组)
{if (栈空 || 栈顶元素大于等于当前比较元素){入栈;}else{while (栈不为空 && 栈顶元素小于当前元素){栈顶元素出栈;更新结果;}当前数据入栈;}
}

例题

1，描叙：有n个人站队，所有的人全部向右看，个子高的可以看到个子低的发型，给出每个人的身高，问所有人能看到其他人发现总和是多少。
输入：4 3 7 1
输出：2
解释：个子为4的可以看到个子为3的发型，个子为7可以看到个子为1的身高，所以1+1=2
思路：观察题之后，我们发现实际上题目转化为找当前数字向右查找的第一个大于他的数字之间有多少个数字，然后将每个结果累计就是答案，但是这里时间复杂度为O(N^2)，所以我们使用单调栈来解决这个问题。

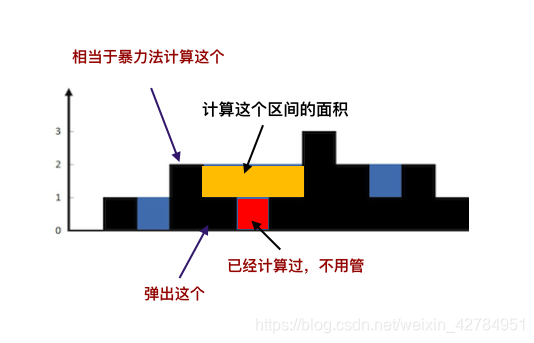
2，接水滴，给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

此题链接力扣题目，官方有给出动画演示，详细的很

    int trap(vector<int>& height) {int  ans=0;int current=0;stack<int >st;while(current<height.size()){while(!st.empty()&&height[current]>height[st.top()]){int t= st.top();st.pop();if(st.empty())break;int dtc=current-st.top()-1;int hght = min(height[current],height[st.top()])-height[t];ans+=dtc*hght;}st.push(current++);}return ans;}

3，柱状图中的最大矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

当前的数字是向两边扩展的，遇到比自己小的元素时出栈是向左扩展自己的边界，遇到自己大的，让大的进栈，向右扩展，记录最大的矩形。

int largestRectangleArea(vector<int>& heights) {heights.push_back(-1);/同理，我们希望栈中所有数据出栈，所以给数组最后添加一个负数stack<int> st;int ret = 0, top;for (int i = 0; i < heights.size(); i++){if (st.empty() || heights[st.top()] <= heights[i]){st.push(i);}else{while (!st.empty() && heights[st.top()] > heights[i]){top = st.top();st.pop();//i-top指的是当前矩形的宽度，heights[top]就是当前的高度//栈中现在为单调递增int tmp = (i - top)*heights[top];if (tmp > ret)ret = tmp;}st.push(top);heights[top] = heights[i];}}return ret;
}

st.push(top); heights[top] = heights[i]; //可能对这两句理解有问题

可以这样子理解，在这里增加了一个宽度为（i-top）,高度为hight[top]的虚拟的柱子，因为，就是后面有满足的区间，他不可能是比这个虚拟的柱子高的，你想，你想，尼好好想，是不是如此尼，哈哈哈哈

3.求最大区间

描述：给出一组数字，求一区间，使得区间元素和乘以区间最小值最大，结果要求给出这个最大值和区间的左右端点
输入：3 1 6 4 5 2
输出：60
3 5

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <stack>
#define ll long long
using namespace std;
const int maxn = 1e5+5;
int a[maxn];
ll sum[maxn];
stack<int> s;
int main(){int days;cin>>days;for(int i=1;i<=days;i++){scanf("%d",&a[i]);sum[i]=sum[i-1]+a[i];}a[days+1]=-1;ll maxa=-1;int pos1,pos2,f;for(int i=1;i<=days+1;i++){if(s.empty()||a[s.top()]<=a[i]) s.push(i);else{while(!s.empty()&&a[s.top()]>a[i]){f=s.top();s.pop();ll	tmp=sum[i-1]-sum[f-1];tmp*=a[f];if(tmp>maxa){maxa=tmp;pos1=f;pos2=i;}}s.push(f);//向前扩展a[f]=a[i];}}printf("%lld\n",maxa);printf("%d %d\n",pos1,pos2-1);return 0;
}

刷题时，扫到盲区了，找到了一个挺好理解这道题的博客

https://www.cnblogs.com/ziyi--caolu/archive/2013/06/23/3151556.html

6
3 1 6 4 5 2

以4为最小值，向左右延伸，6 4 5 值为60.......

思路：解决完为这道题目，我才真正明白了单调栈的原理，它就是以某一个值为最小（最大）值，向这个值的两侧延伸，遇到大于它（小于它）的值，就将它延伸的范围扩大，当然，一般来说，要这样做的算法复杂度为o(n^2)，但是借助栈这个玩意，维护其单调增（减），就可以在o(n)的时间复杂度解决这个问题。将一元素加入栈时，先判断它是否大于(小于)栈顶元素，若是大于（小于）栈顶元素，加入栈。（从这里开始只讲维护单调增栈）否则，将栈顶元素出栈，直到栈顶元素小于要加入栈的元素，在此过程中，需要维护向前延伸和向后延伸的问题，当要加入栈的元素之前有n个栈元素出栈，那么说明这n个出栈的元素都会大于或者等于要入栈的元素，此时，我们需要维护入栈元素可以向前延伸多少个元素（相当于记录它的前面有多少个元素比它大），而每个栈顶元素要向出栈了的元素延伸，因为在出栈了的元素一定是比它的大的元素（根据我维护的是单调增栈）......这样，就在o(n)的时间复杂度内解决了上述问题.........

例如：3 1 6 4 5 2

（3，1，1）（1，2，2）（6，3，3）（4，4，4）（5，5，5）（2，6，6）

首先每个元素自己本身的前后延伸都为1，把3加入栈，1<3，把3出栈，用1的前延伸加上3的前延伸，如此变为（1，1，2），6<1，入栈，变成（1，1，2）（6，3，3），

4<6，将6出栈，4向前延伸，1向后延伸变成（1，1，3）（4，3，4）

5>4，入栈，变成（1，1，3）（4，3，4）（5，5，5）

2<5，5出栈，2向前延伸，4向后延伸，变成（1，1，3）（4，3，5） 2还未入栈（2，5，6）

2<4，4出栈，2向前延伸，1向后延伸，变成（1，1，5）（2，3，6）.....

一次类推，会发现最大的结果在（4，3，5）这里这意味着，以4为最小值的区间范围为3————5，也就是6 4 5

# include<stdio.h>
# include<stack>
#include <iostream>
#define ll long long
using namespace std;
ll sum[100010];
typedef struct
{int x,m;int a,b;
}p;
p a[100010];
stack<p>S;
int main()
{ll i,r,k,n,max,l;scanf("%d",&n);sum[0]=0;for(i=1;i<=n;i++){scanf("%d",&a[i].x);a[i].m=i;a[i].a=i;a[i].b=i;//每个元素都是自身的扩展sum[i]=sum[i-1]+a[i].x;}a[n+1].x=-1;a[n+1].m=n+1;for(i=1;i<=n+1;i++){while(S.empty()==0&&a[i].x<a[S.top().m].x){a[i].a=a[S.top().m].a;//i 向前扩展a[S.top().m].b=i-1;//s.top.m向后扩展S.pop();}S.push(a[i]);}// for(int i=1;i<=n;i++){//   cout<<a[i].x<<" "<<a[i].a<<" "<<a[i].b<<endl;//  }max=-1;for(i=1;i<=n;i++){k=(sum[a[i].b]-sum[a[i].a-1])*a[i].x;if(k>max){max=k;r=a[i].a;l=a[i].b;}}printf("%d\n%d %d",max,r,l);return 0;
}

总结：对单调栈有了一点理解，上述如果有错误，欢迎大佬们指正