单调栈

这是笔者的第一篇博客，由于笔者自身水平的限制。用词可能不够准确，句子不太通顺，代码水平可能也不太行，敬请指出，感激不尽！

我们都知道栈（Stack）是一种先入后出的数据结构，而单调栈建立在栈的基础上，它区别于普通的栈的特殊之处在于

栈中的元素一直保持着单调递增/单调递减的关系

比如单调递增栈中的元素自栈底至栈顶元素（0~n-1）间都是单调递增的，单调递减栈中的元素都是单调递减的。

为了加深印象，我们可以先以单调递减栈为例，看一个例子~

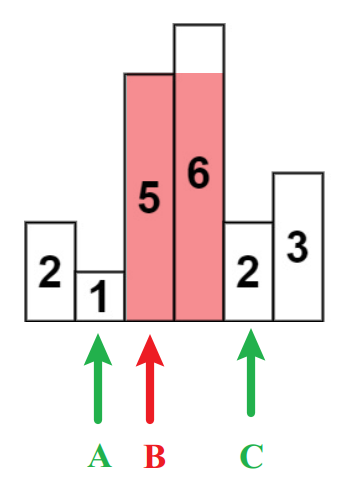
有一组数nums[6] = {10，1，8，12，6，4}按照如下规则进行操作：

如果栈为空/正在处理的数小于栈顶的数，则进栈；
如果正在处理的数大于栈顶的数，则将栈顶元素出栈，然后继续进行判断。

OK，首先我们将栈置空，然后再来一个一个地读数。

首先读到了10，此时栈为空，10进栈，现在栈的状态： {10}
读到了1，栈顶元素为10，1<10，1进栈，栈的状态： {10 ， 1}
读到8，栈顶元素为1，8>1，那么我们将1出栈；

继续判断，8<10，所以8进栈，栈的状态： {10，8}
读到数12，栈顶元素为8，12>8，将8出栈；

继续判断，12>10，所以10出栈，此时栈已为空，将12进栈： {12}
读到6，6<12，进栈；{12，6}
读到4，4<6，将4进栈。 {12，6，4}

读到这边，相信读者对单调栈的基本操作已经稍微有了解啦，那么，单调栈有什么用呢？

还是看上面的例子，假设我们用单调栈处理上面的数组并且得到另外一个数组（假设数组名为arr，并且将该数组初始化为0），规定：在处理每个数（nums[i]）之后，如果nums[i]保持在栈中，则将arr[i]自增1，那么处理完整个数组之后，得到的arr数组应该是：{3，1，1，3，2，1}，不难发现，arr[i]代表的含义是：

自第i个元素开始，从左往右数的连续的比它小的数的个数

通过单调栈的数据结构，我们可以很容易地得到这个数组（很容易知道一个元素附近的数和它之间的大小关系）（只需要O(n)的时间）。所以，如果问题中经常需要判断数组前后元素的大小关系，不妨采用单调栈的数据结构。

这样看可能读者理解不够透彻，印象不够深刻，那不妨一起来看道例题吧~

接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KKSNHLab-1603381702730)(C:\Users\86159\Desktop\rainwatertrap.png)]$

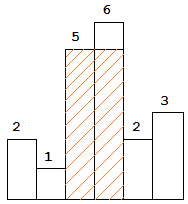
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出：6 解释：上面是由数组
[0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

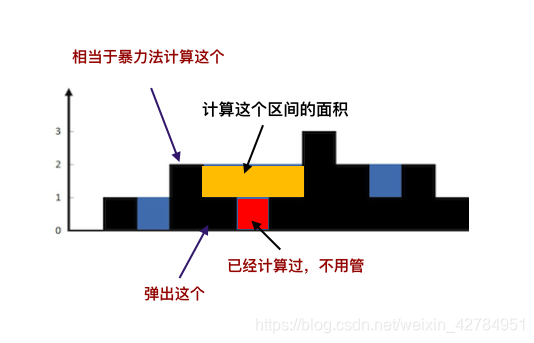
看完题目之后我们可以先来分析一下，按照从左边开始数第i个位置上可以盛放的水的量 = min(该柱子左边最高柱子的高度，该柱子右边最高柱子的高度) - 该柱子的高度。

方法一：

自左往右暴力枚举每个柱子左边最高柱子的高度和右边最高柱子的高度，相加最后可得结果。时间复杂度为O(n²)。

方法二：

不难看出我们需要经常比较每个位置柱子高度和其左右柱子高度，所以不妨建一个单调栈来模拟这个过程：

（为了方便看，我们假设目前读到的柱子高度为heights[i]，栈中存放柱子的编号（自左往右0~n-1）,栈的高度为Size）

若栈为空（Size==0）或柱子高度小于栈顶柱子高度（heights[i] < heights[stack[Size-1]]），则进栈；
若柱子高度大于等于栈底柱子（为此时左边最高的柱子）高度（heights[i] >= heights[stack[0]]），栈中除栈底外的每个格子可以多盛放heights[stack[0]] - heights[stack[j]] 个单位的雨水；
若柱子高度大于栈顶柱子高度且小于栈底柱子高度（heights[i] >= heights[stack[Size-1]]），则栈顶元素对应的柱子可以多盛放heights[i] - heights[stack[Size - 1]]个单位的雨水。（在更新了答案ans的值后，我们不妨令栈顶元素对应的柱子高度等于heights[i]）

就上方第一个例子做个示范：

读入高度heights[0] = 0，进栈。
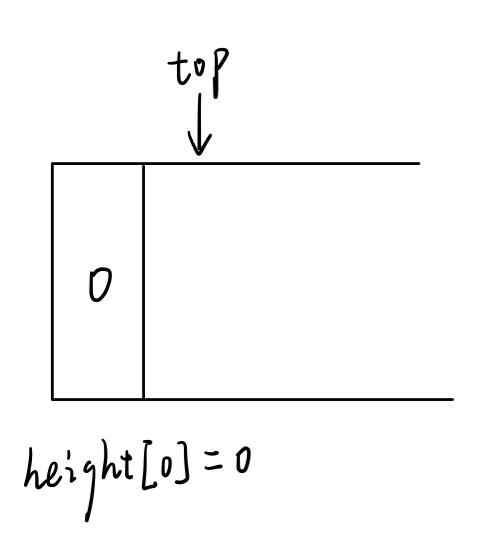
读入高度heights[1] = 1,大于栈底元素，将栈底元素出栈（因为此时栈中只有一个元素，所以不需要对ans进行操作），再将heights[1]进栈。
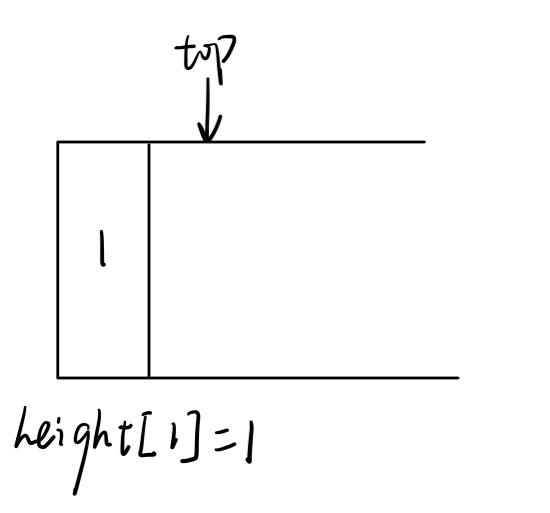
读入元素heights[2] = 0,小于栈顶元素，进栈。
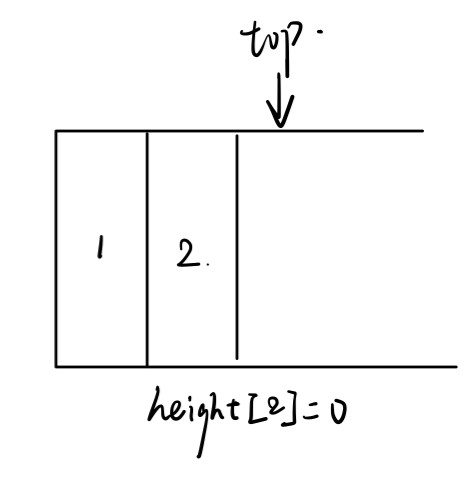
读入元素heights[3] = 2，大于栈底元素，将栈中所有元素弹出，此时因为heights[2] = 0 而 heights[1] = 1 ，所以可以多盛 1-0=1个单位的雨水，将ans + 1。然后将heights[3]进栈。
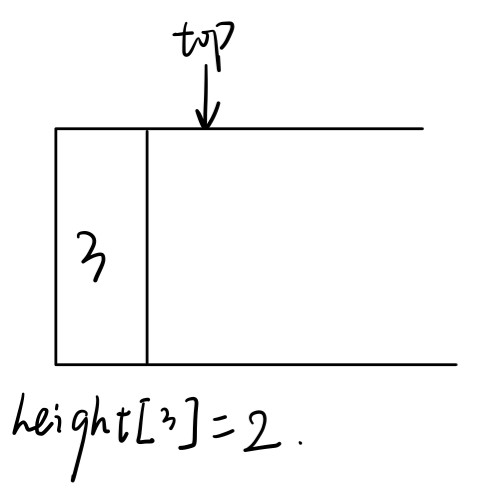
读入元素heights[4] = 1，进栈。读入元素heights[5] = 0，进栈。
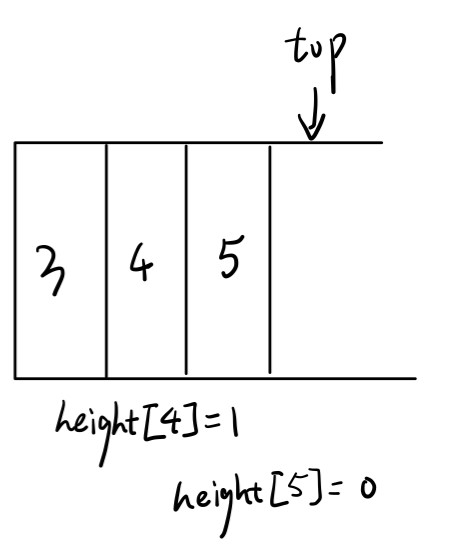
读入元素heights[6] = 1，这里heights[6] > heights[5] 且heights[6] < heights[3] 。我们将ans加上heights[6] - heights[5]之后，令heights[5] = heights[6] 。继续判断，heights[4] = heights[6] 。 heights[6]进栈。
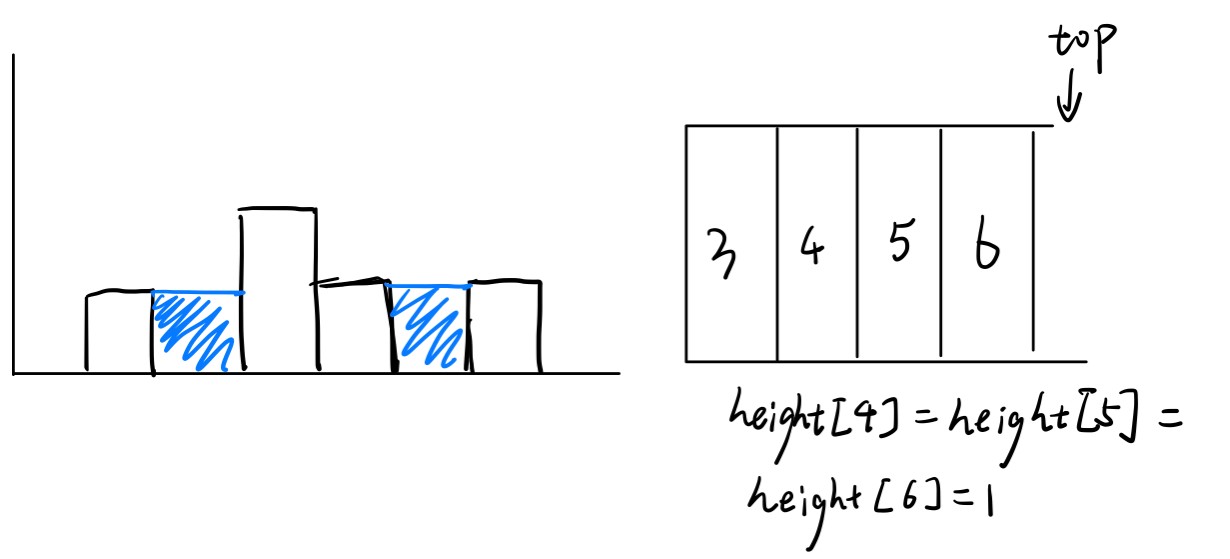
读入元素heights[7] = 3，这里heights[7] > heights[3] （栈底元素）。所以要将栈中所有元素弹出，heights[4]，heights[5]，heights[6] 加上其与heights[3] 的差值，并且更新ans。然后将heights[7]进栈。

后面的步骤都只是重复前面的，所以这边直接跳过。值得注意的是，最后栈中仍有五个元素，但因为右边是空的，无法盛水，所以无需出栈，保持原样即可。

代码实现（C语言）：

int trap(int* height, int heightSize){int stack[1000];int top = 0,i;int ans = 0;for(i=0;i<heightSize;i++){if(top==0){	//如果栈为空，直接进栈stack[0] = i;top++;}else if(height[i] >= height[stack[0]]){ //如果读到元素大于栈底元素高度，将栈置空后进栈int j;for(j=1;j<top;j++){ans += height[stack[0]] - height[stack[j]];height[stack[j]] = heights[stack[0]]}stack[0] = i;top = 1;}else{int j=1;while(height[i]>height[stack[top-j]]){ ans += height[i] - height[stack[top-j]];height[stack[top-j]] = height[i];j++;}stack[top] = i;top++;}}return ans;
}

限于笔者的水平，文章或者代码中可能存在错误或者疏漏，请读者不吝指正，感激不尽！