单调栈

单调栈：栈内的元素按照某种方式排序下单调递增或单调递减，如果新入栈的元素破坏的单调性，就弹出栈内元素，直到满足单调性。

单调栈分为单调递增栈和单调递减栈：

• 单调递增栈：栈中数据入栈或出栈的序列为单调递减序列；
• 单调递减栈：栈中数据入栈或出栈的序列为单调递增序列。

维护单调递增栈

• 遍历数组中每一个元素，执行入栈：每次入栈前先检验栈顶元素和进栈元素的大小。
• 如果栈空或进栈元素大于栈顶元素则直接入栈；如果进栈元素小于等于栈顶元素，则出栈，直至进栈元素大于栈顶元素。

 //单调递增栈Stack<Integer> stack = new Stack();for (int i = 0; i < nums.length; i++) {while (!stack.isEmpty() && nums[i] <= stack.peek()) {stack.pop();}stack.push(nums[i]);}

维护单调递减栈

• 遍历数组中每一个元素，执行入栈：每次入栈前先检验栈顶元素和进栈元素的大小。
• 如果栈空或进栈元素小于栈顶元素则直接入栈；如果进栈元素大于等于栈顶元素，则出栈，直至进栈元素小于栈顶元素。

//单调递减栈Stack<Integer> stack = new Stack();for (int i = 0; i < nums.length; i++) {while (!stack.isEmpty() && nums[i] >= stack.peek()) {stack.pop();}stack.push(nums[i]);}

单调栈的作用

以O(N)的时间复杂度求出某个数的左边或右边第一个比它大或小的元素。

1、求第i个数左边第一个比它小的元素的位置

从左到右遍历元素构造单调递增栈：一个元素左边第一个比它小的数的位置就是将它插入单调递增栈时的栈顶元素，若栈为空，则说明不存在这样的数。

举例来说，nums=[5,4,3,4,5]，初始时栈空stack=[]

• i=0：栈空，左边没有比它小的元素，同时下标0入栈，stack=[0]；
• i=1：当前元素4小于栈顶元素对应的元素5，故将栈顶弹出，此时栈空，下标1入栈，stack=[1]；
• i=2：当前元素3小于栈顶元素对应的元素4，故将栈顶弹出，此时栈空，下标2入栈，stack=[2]；
• i=3：当前元素4大于栈顶元素对应的元素3，下标3入栈，stack=[2,3]；
• i=4：当前元素5等于栈顶元素对应的元素4，下标4入栈，stack=[2,3,4]；

2、求第i个数左边第一个比它大的元素的位置

从左到右遍历元素构造单调递减栈：一个元素左边第一个比它大的数的位置就是将它插入单减栈时栈顶元素的值，若栈为空，则说明不存在这样的数。

3、求第i个数右边第一个比它小的元素的位置

从右到左遍历元素构造单调递增栈：一个元素右边第一个比它小的数的位置就是将它插入单增栈时栈顶元素的值，若栈为空，则说明不存在这样的数。

从左到右遍历元素构造单调递增栈：一个元素右边第一个比它小的数的位置就是将它弹出栈时即将入栈的元素，如果没被弹出栈，说明不存在这样的数。

4、求第i个数右边第一个比它大的元素的位置

从右到左遍历元素构造单调递减栈：一个元素右边第一个比它大的数的位置就是将它插入单减栈时栈顶元素的值，若栈为空，则说明不存在这样的数。

从左到右遍历元素构造单调递减栈：一个元素右边第一个比它大的数的位置就是将它弹出栈时即将入栈的元素的下标，如果没被弹出栈，说明不存在这样的数。

实战

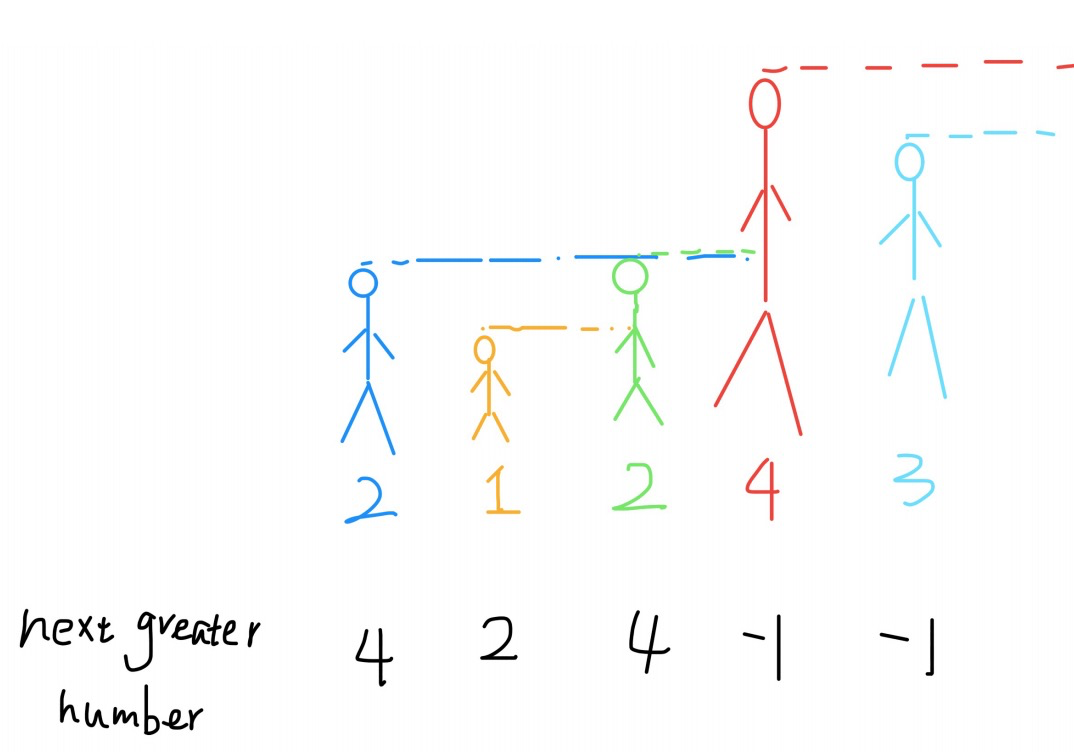
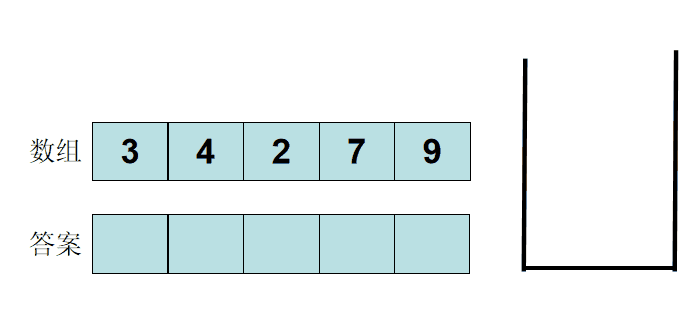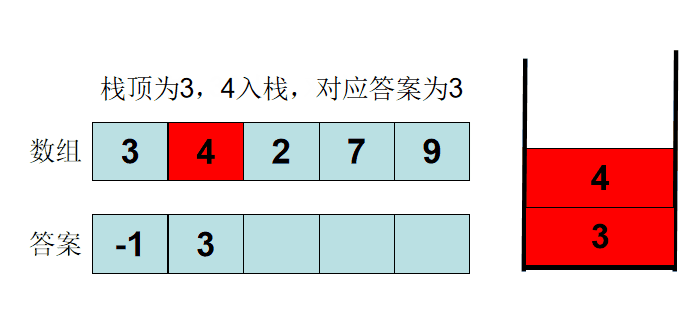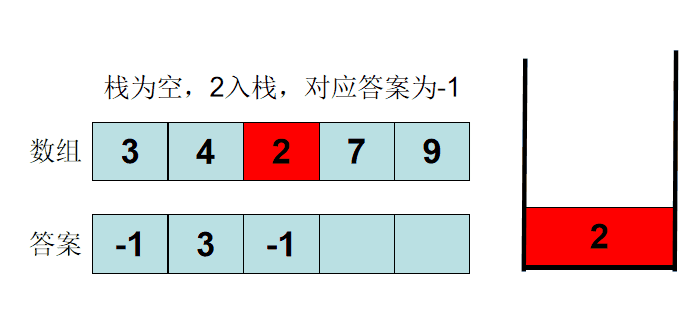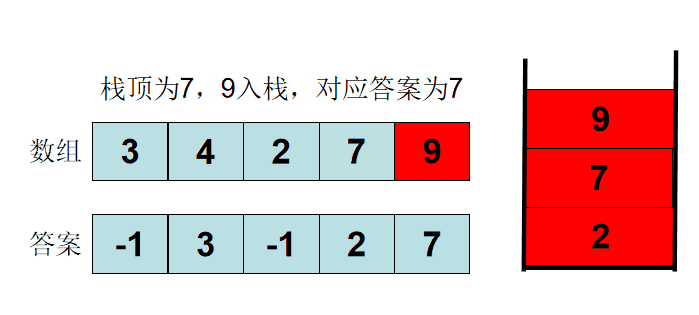
例题：给你⼀个数组，返回⼀个等⻓的数组，对应索引存储着下⼀个更⼤元素，如果没有更⼤的元素，就存-1。直接上⼀个例⼦： 给⼀个数组 [2,1,2,4,3]，需要返回数组 [4,2,4,-1,-1]。
解释：第⼀个2大的后面的数4; 比1⼤的后面的数是2；第⼆个2后⾯⽐2⼤的数是4; 4后⾯没有⽐4⼤的数，填-1；3后⾯没有⽐3⼤的数，填-1。

这道题的暴⼒解法很好想到，就是对每个元素后⾯都进⾏扫描，找到第⼀个 更⼤的元素就⾏了。但是暴⼒解法的时间复杂度是O(n^2)。

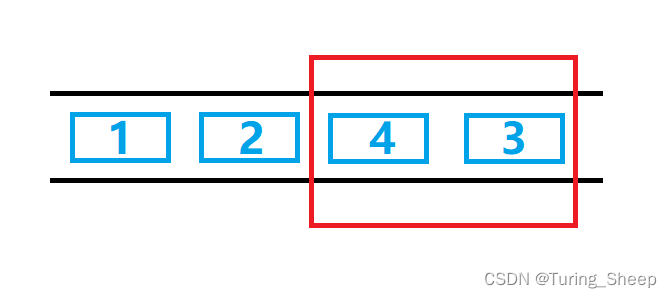
用单调栈来解决更高效。这个问题可以这样抽象思考：把数组的元素想象成并列站⽴的⼈，元素⼤⼩想象成⼈的⾝⾼。这些⼈⾯对你站成⼀列，如何求元素「2」的Next Greater Number呢？很简单，如果能够看到元素「2」，那么他后⾯可⻅的第⼀个 ⼈就是「2」的 Next Greater Number，因为⽐「2」⼩的元素⾝⾼不够，都被 「2」挡住了，第⼀个露出来的就是答案。

public int[] nextGreaterNumber(int[] nums) {Stack<Integer> s = new Stack<>();int[] ans = new int[nums.length];for (int i = nums.length - 1; i >= 0; i--) {while (!s.isEmpty() && s.peek() <= nums[i]) {s.pop();}//栈顶元素就是右边第1个比nums[i]更大的元素ans[i] = (s.isEmpty()) ? -1 : s.peek();s.push(nums[i]);}return ans;
}

leetcode样题

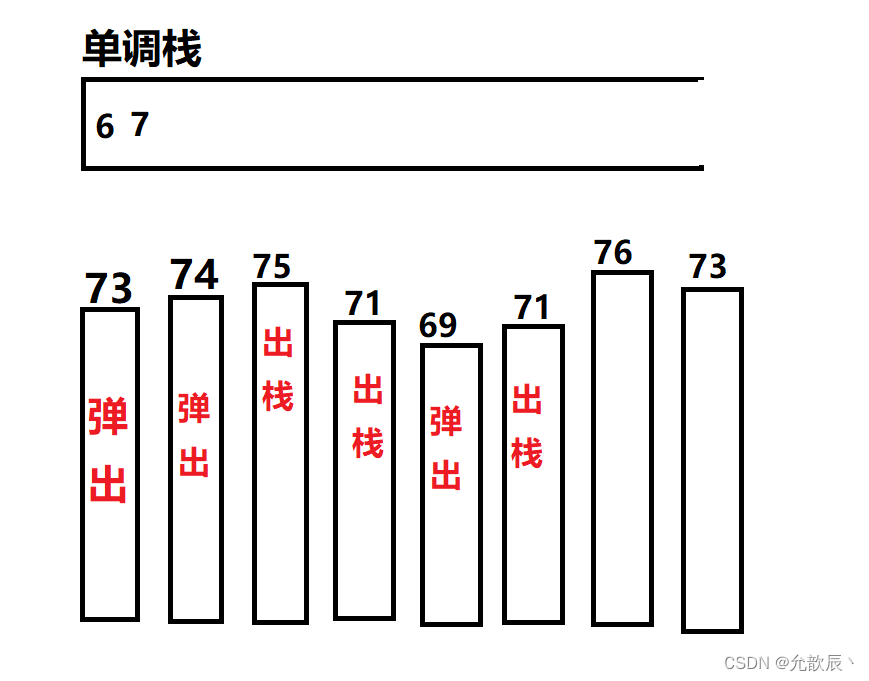
请根据每日气温列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

问题转化：求元素右边第一个比它大的元素下标，可以从右至左遍历，维护一个存储下标的单调递减栈。

public int[] dailyTemperatures(int[] temperatures) {int[] result = new int[temperatures.length];//单调递减栈Stack<Integer> stack = new Stack();for (int i = temperatures.length - 1; i >= 0; i--) {while (!stack.isEmpty() && temperatures[i] >= temperatures[stack.peek()]) {stack.pop();}if (stack.isEmpty()) {result[i] = 0;} else {result[i] = stack.peek() - i;}stack.push(i);}return result;
}

leetcode样题
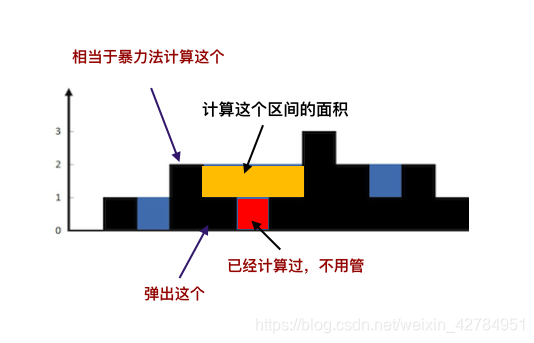
柱状图中最大的矩形
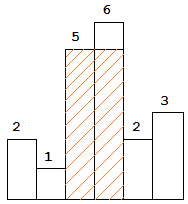
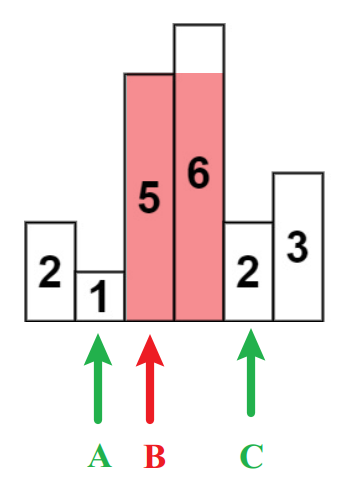
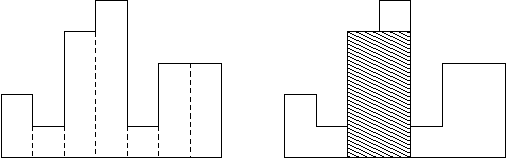
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例：
输入: [2,1,5,6,2,3]
输出: 10

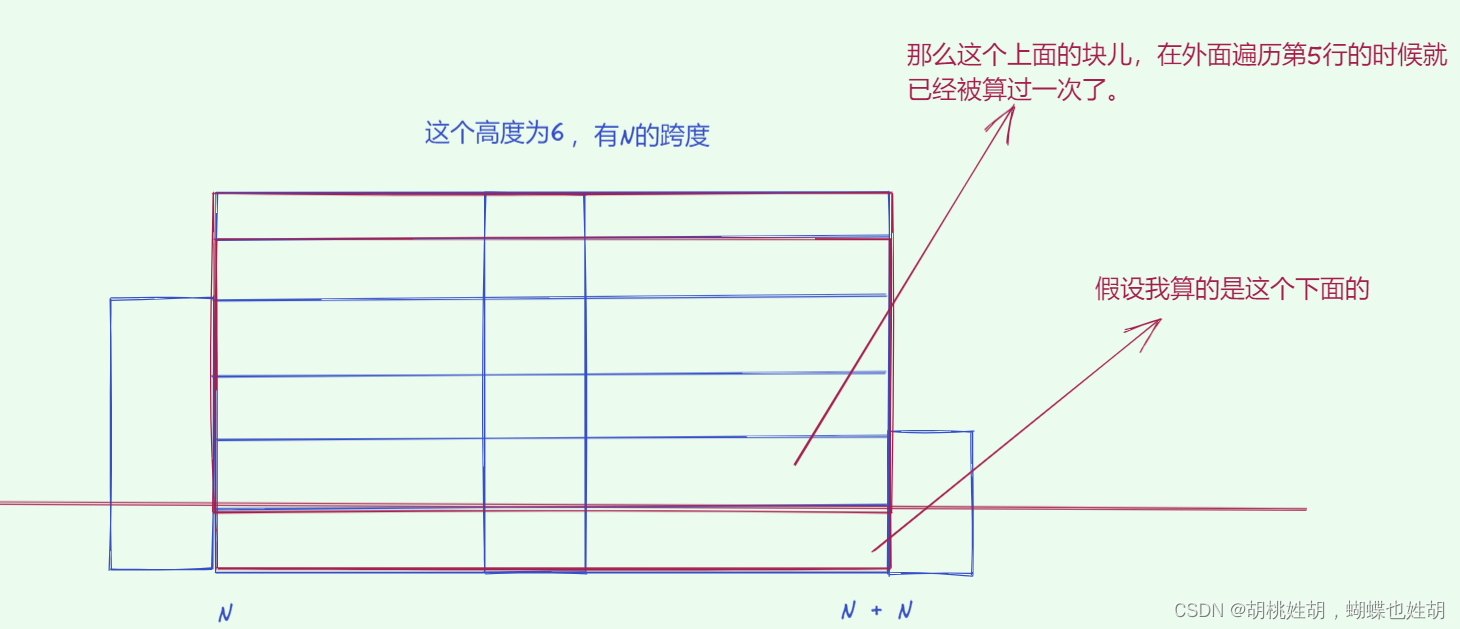
class Solution {public int largestRectangleArea(int[] heights) {Stack<Rect> stack = new Stack<>();int maxArea = 0;//从左到右遍历，维护一个单调递增栈for (int i = 0; i < heights.length; i++) {int accumulatedWidth = 0;while (!stack.isEmpty() && stack.peek().height >= heights[i]) {Rect peekRect = stack.peek();accumulatedWidth += peekRect.width;maxArea = Math.max(maxArea, peekRect.height * accumulatedWidth);stack.pop();}stack.push(new Rect(heights[i], accumulatedWidth + 1));}//如果heights = {1,2,3}那么以上循环就一直push，不会出栈，下面这段处理这种情况，强制出栈int accumulatedWidth = 0;while (!stack.isEmpty()) {Rect peekRect = stack.peek();accumulatedWidth += peekRect.width;maxArea = Math.max(maxArea, peekRect.height * accumulatedWidth);stack.pop();}return maxArea;}class Rect {private int height;private int width;Rect(int height, int width) {this.height = height;this.width = width;}}
}

leetcode样题
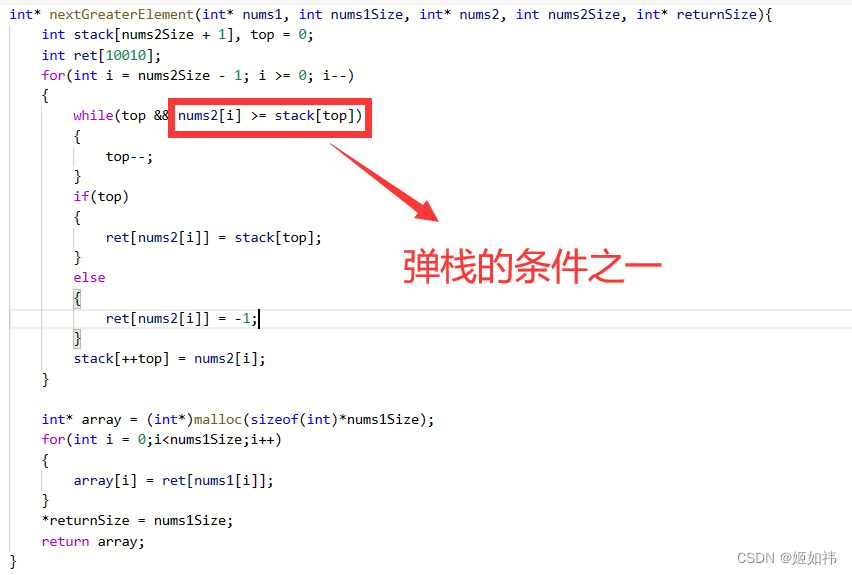
下一个更大的元素
给你两个没有重复元素的数组nums1和nums2 ，其中nums1是 nums2的子集。请你找出nums1中每个元素在nums2中的下一个比其大的值。nums1中数字x的下一个更大元素是指x在nums2中对应位置的右边的第一个比x大的元素。如果不存在，对应位置输出-1。

输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]

对于num1中的数字4，你无法在第二个数组中找到下一个更大的数字，因此输出-1。
对于num1中的数字1，第二个数组中数字1右边的下一个较大数字是3。
对于num1中的数字2，第二个数组中没有下一个更大的数字，因此输出-1。

思路

• 先对 nums2 中的每一个元素，求出它的右边第一个更大的元素；
• 将上一步的对应关系放入哈希表（HashMap）中；
• 再遍历数组 nums1，根据哈希表找出答案。

public int[] nextGreaterElement(int[] nums1, int[] nums2) {Stack<Integer> stack = new Stack<>();//key为nums1中的元素，value为nums1中在key的右边第1个比key大的元素Map<Integer, Integer> map = new HashMap<>();for (int j = nums2.length - 1; j >= 0; j--) {//构造单调递减栈while (!stack.isEmpty() && stack.peek() <= nums2[j]) {stack.pop();}if (!stack.isEmpty()) {map.put(nums2[j], stack.peek());}stack.push(nums2[j]);}int[] res = new int[nums1.length];//遍历nums1，从map中找答案for (int i = 0; i < nums1.length; i++) {res[i] = map.getOrDefault(nums1[i], -1);}return res;
}

单调队列

单调队列与单调栈极其相似，把单调栈先进后出的性质改为先进先出即可。
单调队列：队列中元素之间的关系具有单调性，而且队首和队尾都可以进行出队操作，只有队尾可以进行入队操作。

在队尾入队的时候维护单调性。

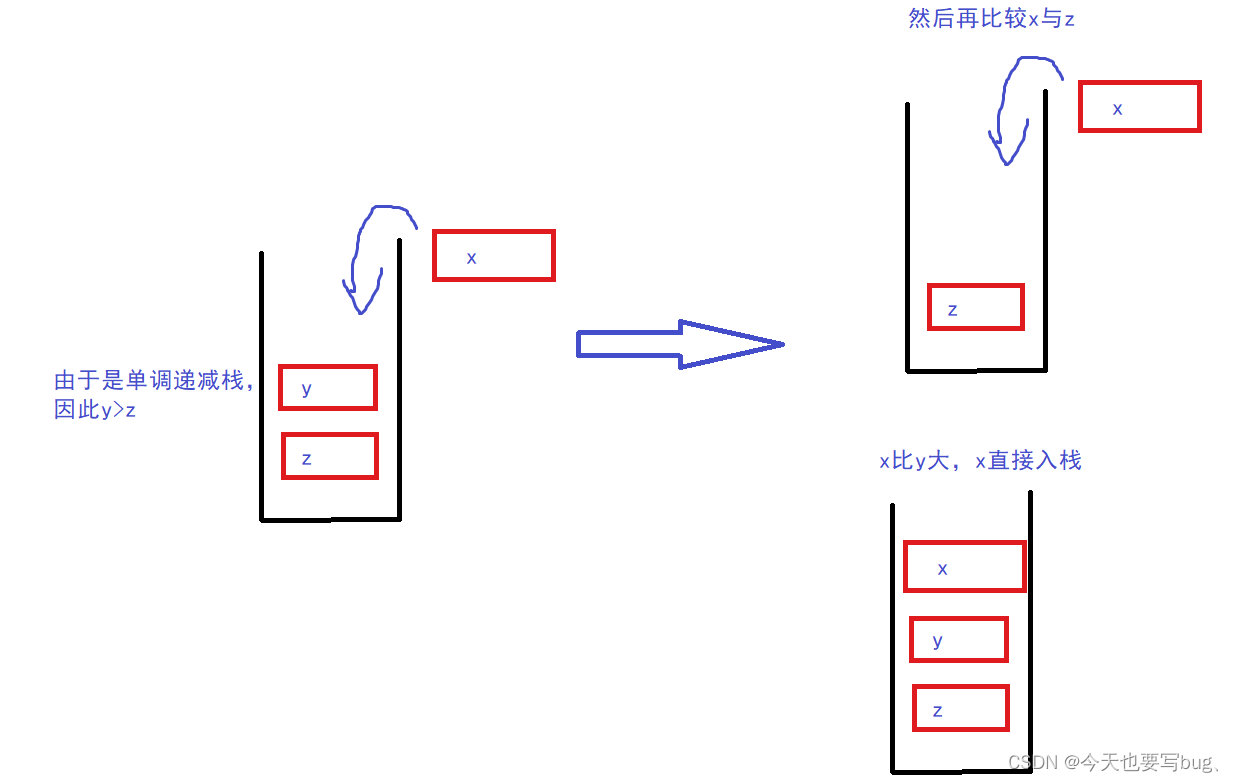
• 对于单调递增队列，设当前准备入队的元素为e，从队尾开始把队列中的元素逐个与e对比，把比e大或者与e相等的元素逐个删除，直到遇到一个比e小的元素或者队列为空为止，然后把当前元素e插入到队尾。
• 对于单调递减队列也是同样道理，只不过从队尾删除的是比e小或者与e相等的元素。

维护单调队列

以维护一个单调递减队列为例

• 遍历数组中每一个元素，执行入队：每次入队前先检验队尾元素和即将进入队列元素的大小。
• 如果队列空或进队元素小于队尾元素则直接入队；如果进队元素大于等于队尾元素，则将队尾元素从队尾出队，直至进队元素小于队尾元素或队列空为止。

//使用双端队列
Deque<Integer> deque = new ArrayDeque<>();
//维护单调递减队列，队头是最大元素，从队尾出队
for (int i = 0; i < nums.length; i++) {while (!deque.isEmpty() && nums[i] >= deque.getLast()) {deque.pollLast();}deque.offerLast(nums[i]);
}

单调队列的作用主要在于求区间最小（最大）值问题。

leetcode样题
滑动窗口最大值
给你一个整数数组nums，有一个大小为k的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的k个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置 最大值

---

[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7

思路
遍历数组，将数存放在双向队列中，并用L和R来标记窗口的左边界和右边界。队列中保存的并不是真的数，而是该数值对应的数组下标位置，并且队列的数（即下标对应的元素）要从大到小排序。如果当前遍历的数比队尾的值大，则需要弹出队尾值，直到队列重新满足从大到小的要求。刚开始遍历时，L和R都为0，有一个形成窗口的过程，此过程没有最大值，L不动，R向右移。当窗口大小形成时，L 和R一起向右移，每次移动时，判断队首的值的数组下标是否在 [L,R]中，如果不在则需要弹出队首的值，当前窗口的最大值即为队首的数。

初始状态：L=R=0,队列:{}
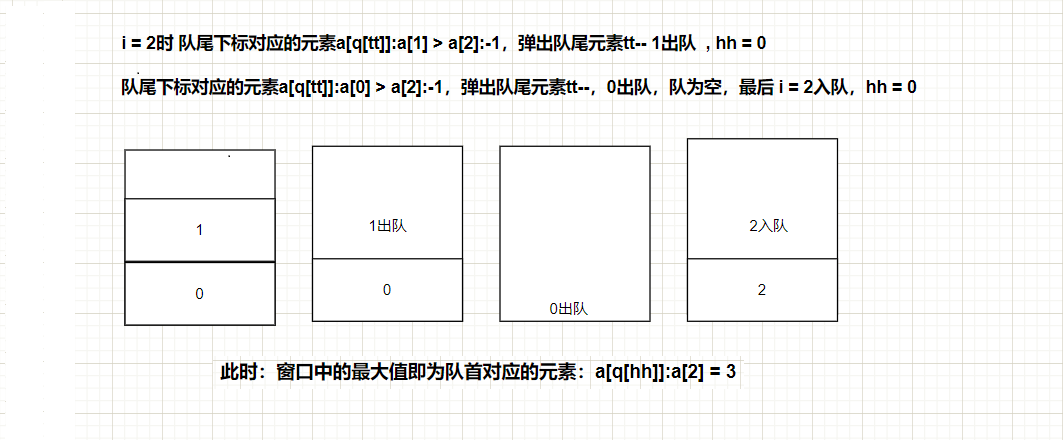
i=0,nums[0]=1。队列为空,直接加入。队列：{1}
i=1,nums[1]=3。队尾值为1，3>1，弹出队尾值，加入3。队列：{3}
i=2,nums[2]=-1。队尾值为3，-1<3，直接加入。队列：{3,-1}。此时窗口已经形成，L=0,R=2，result=[3]
i=3,nums[3]=-3。队尾值为-1，-3<-1，直接加入。队列：{3,-1,-3}。队首3对应的下标为1，L=1,R=3，有效。result=[3,3]
i=4,nums[4]=5。队尾值为-3，5>-3，依次弹出后加入。队列：{5}。此时L=2,R=4，有效。result=[3,3,5]
i=5,nums[5]=3。队尾值为5，3<5，直接加入。队列：{5,3}。此时L=3,R=5，有效。result=[3,3,5,5]
i=6,nums[6]=6。队尾值为3，6>3，依次弹出后加入。队列：{6}。此时L=4,R=6，有效。result=[3,3,5,5,6]
i=7,nums[7]=7。队尾值为6，7>6，弹出队尾值后加入。队列：{7}。此时L=5,R=7，有效。result=[3,3,5,5,6,7]

解释一下为什么队列中要存放数组下标而不是直接存储数值，因为要判断队首的值是否在窗口范围内，由数组下标取值很方便，而由值取数组下标不是很方便。

public int[] maxSlidingWindow(int[] nums, int k) {int[] res = new int[nums.length - k + 1];int index = 0;//双端队列 保证队列中数组位置的数值按从大到小排序Deque<Integer> deque = new ArrayDeque<>();for (int i = 0; i < nums.length; i+=1) {// 保证从大到小 如果前面数小则需要依次弹出，直至满足要求while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {deque.pollLast();}// 添加当前值对应的数组下标deque.offerLast(i);//判断当前队列中队首的值是否有效，是否还在窗口中if (!deque.isEmpty() && deque.getFirst() <= i - k){deque.pollFirst();}// 当窗口长度为k时，即窗口形成时，保存当前窗口中最大值if (i >= k - 1) {res[index++] = nums[deque.getFirst()];}}return res;}

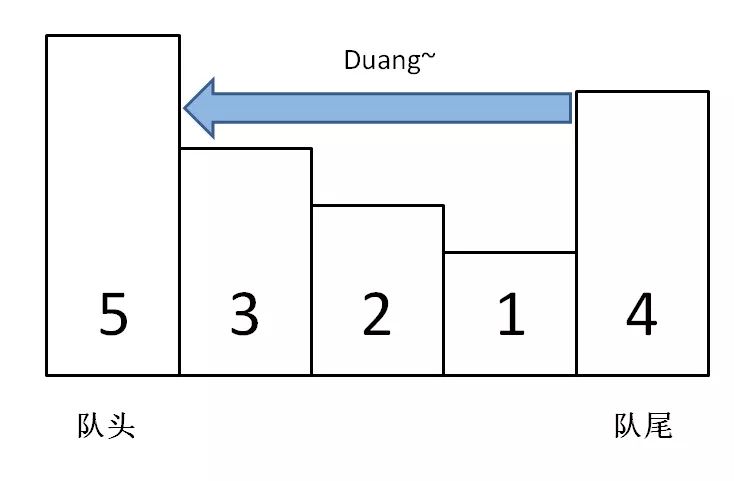
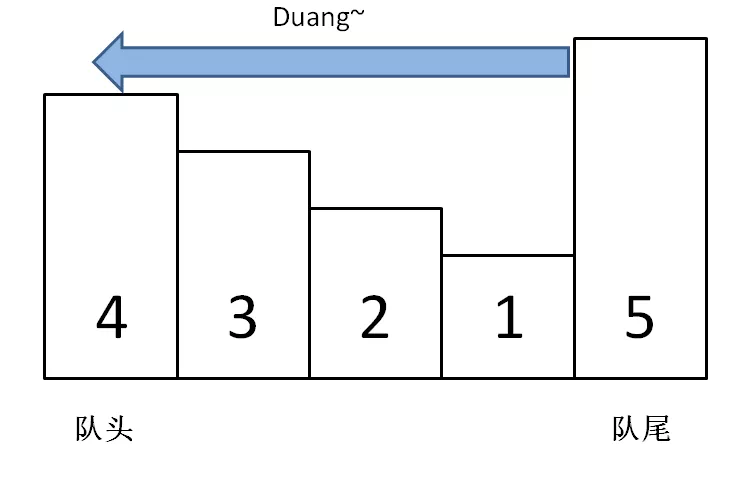
在一堆数字中，已知最值是A，如果给这堆数字添加一个数字B，那么比较一下A和B就可以立即算出新的最值；但如果减少一个数，就不能直接得到最值了，因为如果减少的这个数恰好是A，就需要遍历所有数重新找最值。回到这道题的场景，每个窗口前进的时候，要添加一个数同时减少一个数，所以想在O(1)的时间内得出新的最值，不是那么容易，需要单调队列这种特殊的数据结构来辅助。

单调队列」的核心思路和「单调栈」类似，push方法依然在队尾添加元素，但是要把前面比自己小的元素都删掉。你可以想象，加入数字的大小代表人的体重，把前面体重不足的都压扁了，直到遇到更大的量级才停住。

// 单调递减队列
class MonotonicQueue {Deque<Integer> deque;public MonotonicQueue() {deque = new ArrayDeque<>();}public void push(int val) {// 如果当前要入队的数字比队尾数字还大，一直出队直到队空或遇到更大的元素// 保持从队头到队尾的单调递减性质while (!deque.isEmpty() && deque.getLast() < val) {deque.pollLast();}deque.offerLast(val);}
}

如果每个元素被加入时都这样操作，最终单调队列中的元素大小就会保持一个单调递减的顺序，因此我们的max方法可以可以这样写。

public int getMax() {return deque.getFirst();
}

pop方法在队头删除元素n，也很好写。之所以要判断deque.getFirst() == val，是因为我们想删除的队头元素n可能已经被「压扁」了，可能已经不存在了，所以这时候就不用删除了。

// 如果val等于队头，即等于最大值，就删除
public void pop(int val) {if (!deque.isEmpty() && deque.getFirst() == val) {deque.pollFirst();}
}

至此，单调队列设计完毕，看下完整的解题代码：

// 单调递减队列
class MonotonicQueue {Deque<Integer> deque;public MonotonicQueue() {deque = new ArrayDeque<>();}public void push(int val) {// 如果当前要入队的数字比队尾数字还大，一直出队直到队空或遇到更大的元素// 保持从队头到队尾的单调递减性质while (!deque.isEmpty() && deque.getLast() < val) {deque.pollLast();}deque.offerLast(val);}// 如果val等于队头，即等于最大值，就删除public void pop(int val) {if (!deque.isEmpty() && deque.getFirst() == val) {deque.pollFirst();}}public Integer getMax() {return deque.getFirst();}
}public int[] maxSlidingWindow(int[] nums, int k) {MonotonicQueue window = new MonotonicQueue();List<Integer> res = new ArrayList<>();for (int i = 0; i < nums.length; i++) {if (i < k - 1) {// 先填满前k-1window.push(nums[i]);continue;}// 再加入最后一个window.push(nums[i]);// i大于或等于k - 1,窗口饱合// 取出最大值res.add(window.getMax());// 如果要删除的元素nums[i - k + 1]，不是最大值，不影响后面的判断，不删除也可以window.pop(nums[i - k + 1]);}int[] ans = new int[res.size()];for (int i = 0; i < res.size(); i++) {ans[i] = res.get(i);}return ans;
}