一、单调栈

1、什么是单调栈？

单调栈顾名思义就是栈中的元素是具有单调性的，比如依次增大的数则具有单调递增的性质，依次减小的数则具备单调递减的性质。

2、单调栈的模板

（1）问题：

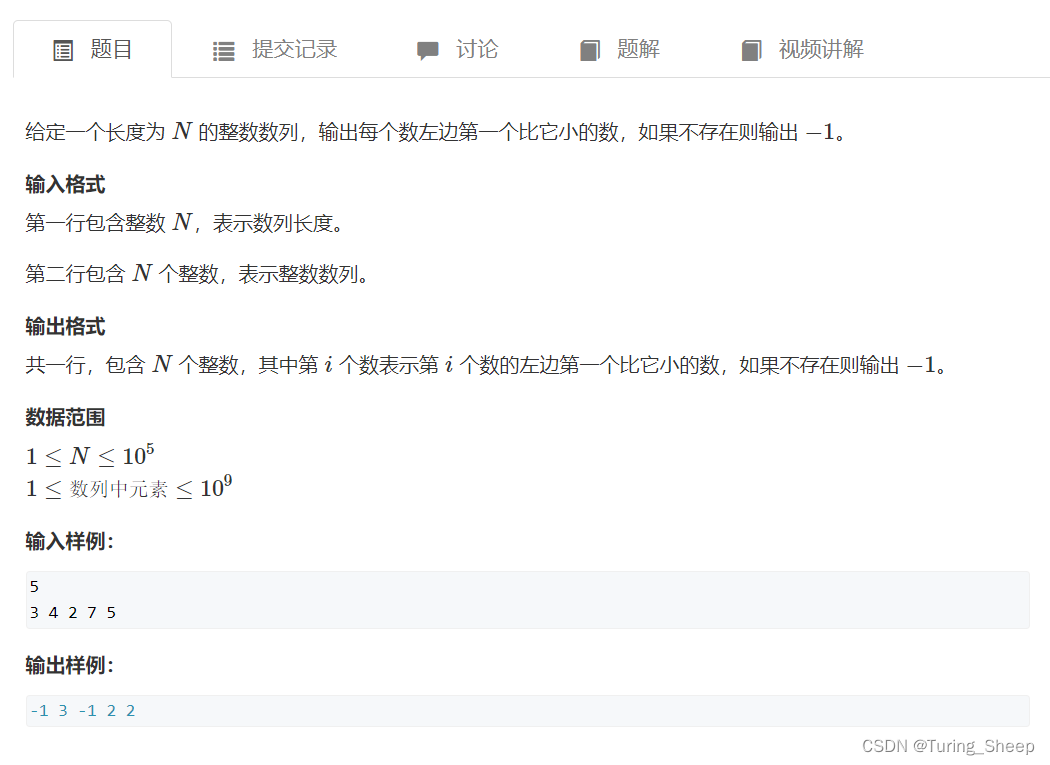
（2）分析：

我们可以写出一个暴力做法：如下：

#include<iostream>
using namespace std;
const int N=100010;
int a[N];
int main()
{int n;cin>>n;for(int i=0;i<n;i++){scanf("%d",a+i);}for(int i=0;i<n;i++){int j,flag=0;for(j=i-1;j>=0;j--){if(a[j]<a[i]){flag=1;break;}}if(flag)cout<<a[j]<<" ";else cout<<-1<<" ";}return 0;
}

但是这种暴力做法的时间复杂度是O(N²)，因此当我们提交的时候会发生超时的情况。因此，我们需要寻找另外的算法来优化时间复杂度。

此时，我们可以采用空间换时间的思想，具体思路如下：

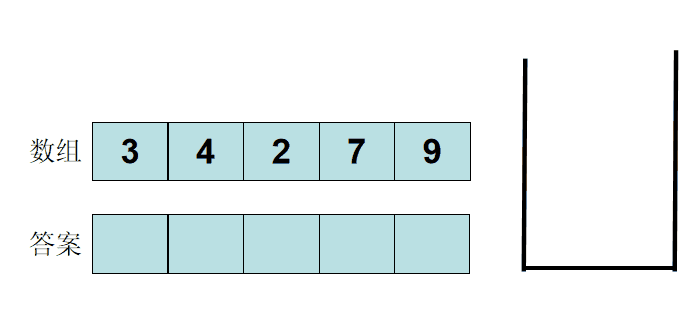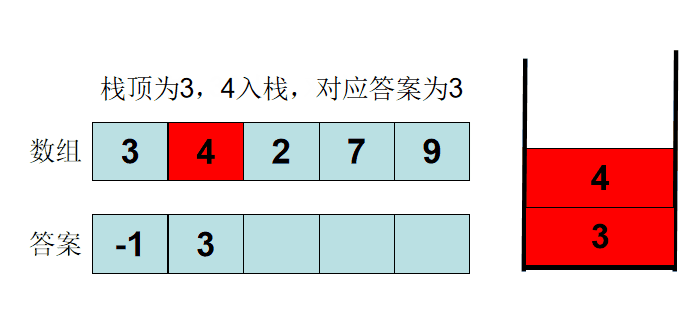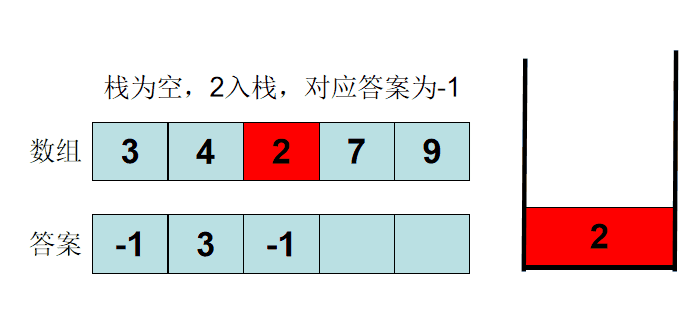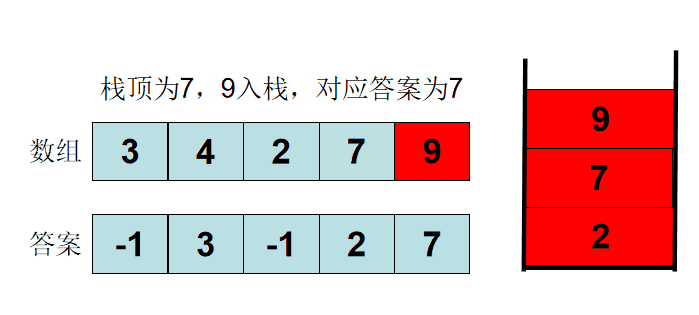
我们除了创建一个数组去存储输入的数据外，我们再开辟一块空间来处理数据。题目中提到的是左端的第一个，此时我们很容易就联想到了栈这种数据结构，因为这种数据结构是先进后出，假设我们再存储到数组中的同时，也存储到栈中，那么我们的栈顶元素一定是前距离a[i]左端最近的数字。

因此，当我们使用栈的时候，就能够保证我们输出的栈顶元素是距离目标元素最近的，那么我们接下来的问题就是如何保证，我们输出的栈顶元素一定是比目标元素小呢？

我们看下面的思路：

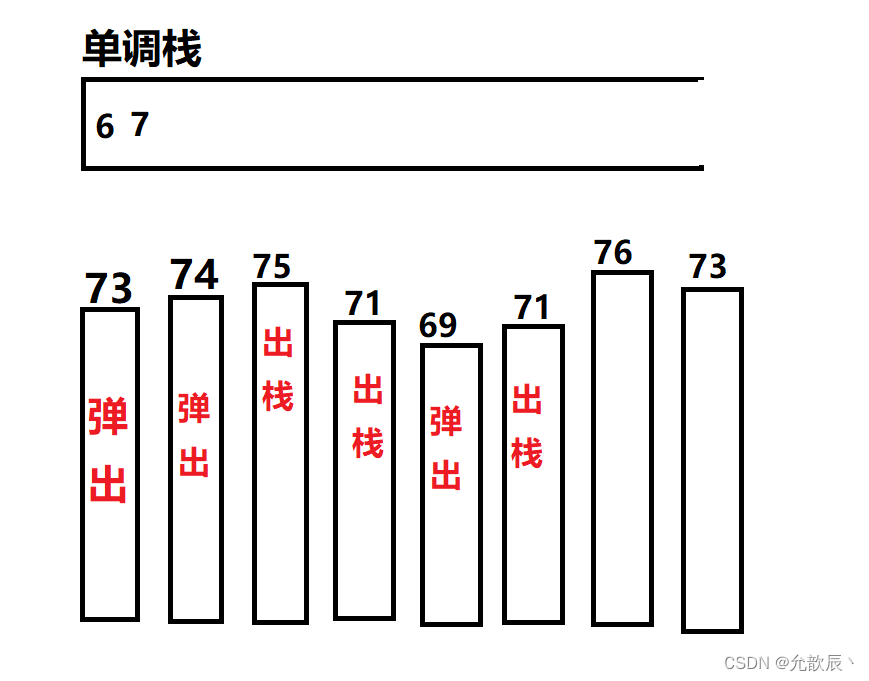
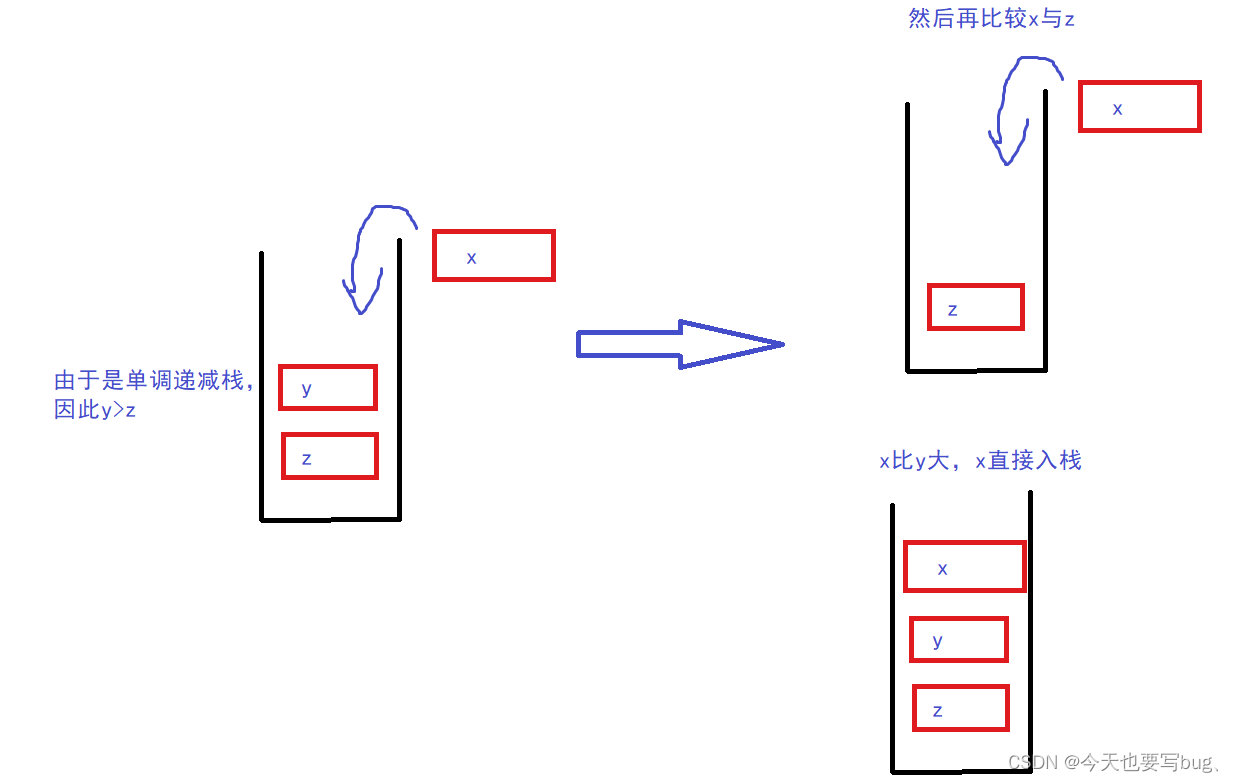
• step1 : 在栈不为空的条件下，只要栈顶元素大于等于栈顶元素，那么我们就删除掉栈顶元素。
• step2 : 让目标元素进栈。

然后我们来分析一下上面的思路：
步骤一就保证了栈中的任意一个元素，一定是小于后一个元素的。所以此时栈中的元素呈现了单调递增的特性。

接着我相信大家会在两个点上感到疑惑：

1、删除的元素会不会是后续过程中的答案？

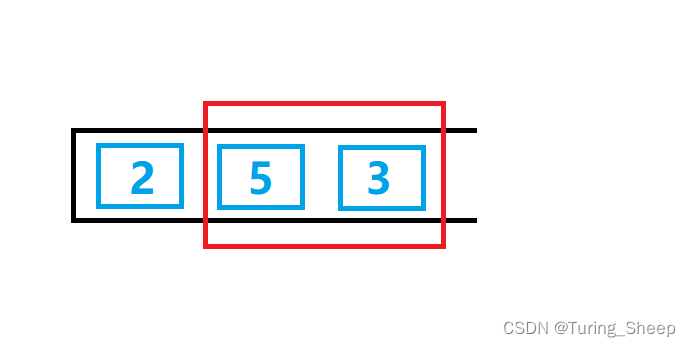
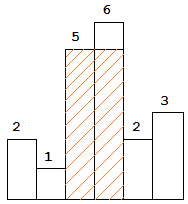
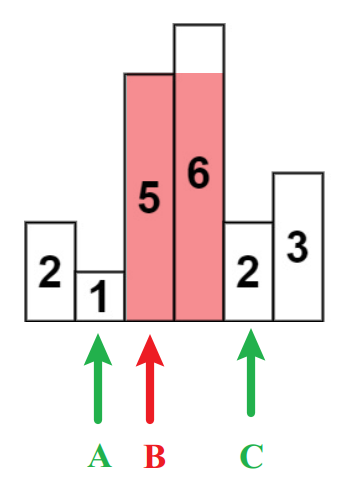
我们看下面的这种情况下，5是否有可能成为后续过程的答案？
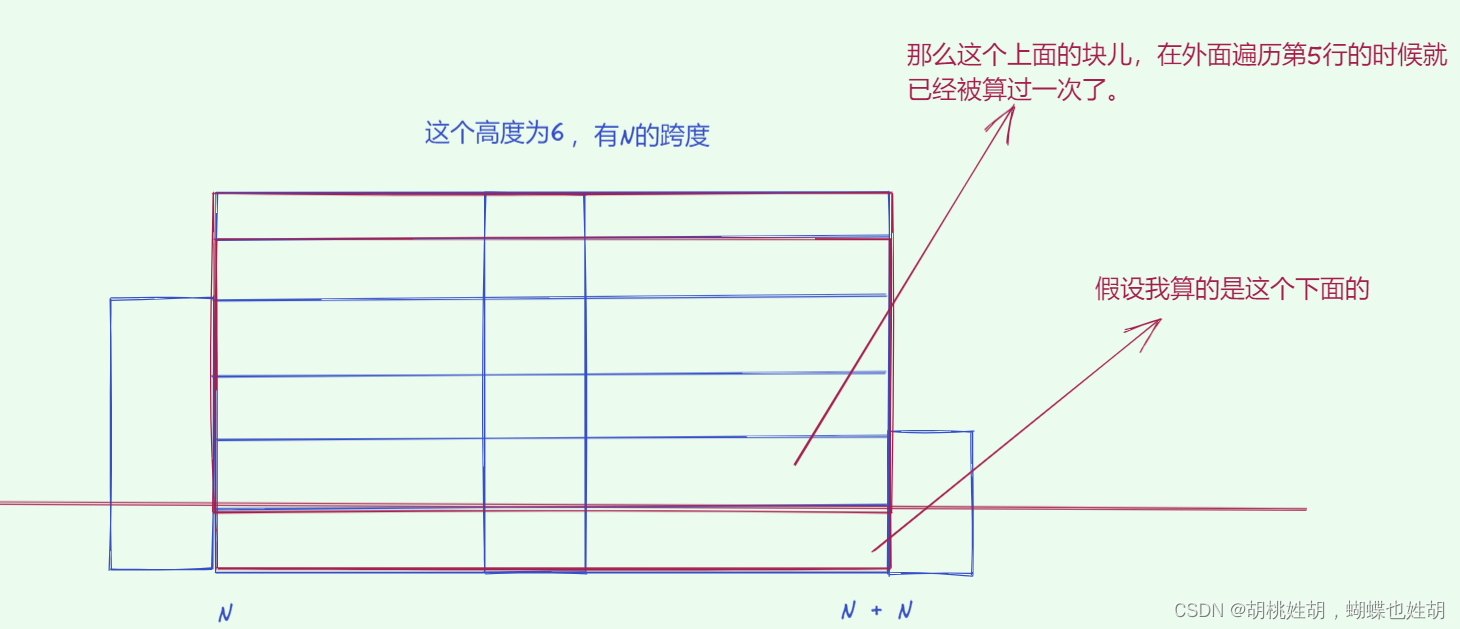
假设我们的目标元素是6，那么5小于6，但是由于5>3，根据不等式的传递性，3也小于6，但是3距离元素6更近，所以3一定是答案。那么这是数字3存在的情况。我们假设数字3被删除了，我们假设3遇到了2,此时3大于等于2，所以3会被删除，但是此时入栈的元素是不是2,很明显再2的存在下，5更不可能成为答案。综上所述，我们删除的元素是不可能成为答案的。

2、目标元素一定要入栈吗？

答案是一定的，因为通过步骤一的循环处理，栈具备单调递减的特点，因此我们的目标元素就会成为栈中最小的元素，同时这个元素还是距离下一个元素最近的。假设这个元素都大于目标元素，那么剩余元素必定大于目标元素，所以这个栈中就不会再存在答案了。综上所述，我们的目标元素是最有可能成为下一次判断时的答案。

因此，我们的思路一定能够输出正确的答案，那么我们如何实现呢？

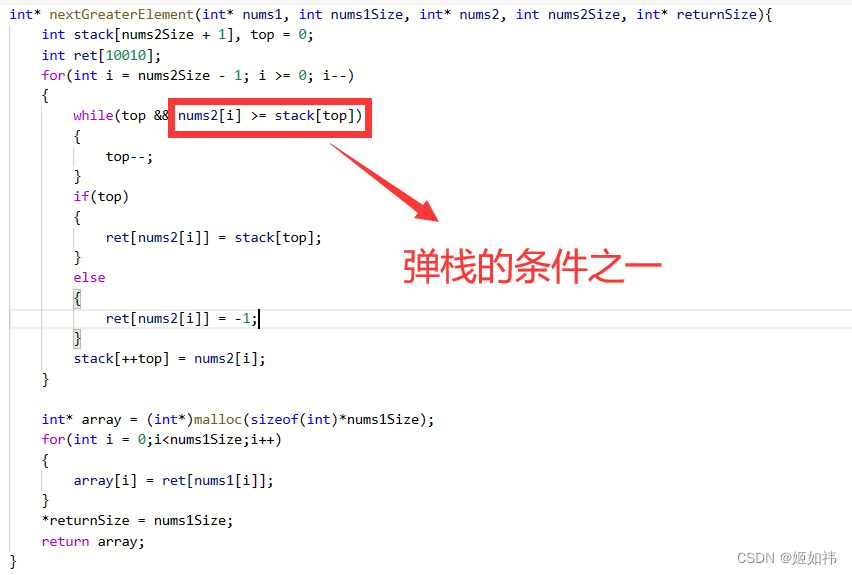
#include<iostream>
using namespace std;
const int N=100010;
int a[N],stk[N],top;
int main()
{int n;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",a+i);while(stk&&stk[top]>=a[i])top--;if(!top)cout<<-1<<" ";else cout<<stk[top]<<" ";stk[++top]=a[i];}return 0;
}

我们发现上面的时间复杂度是O(N)，大大的优化了时间。

二、单调队列

1、什么是单调队列

单调队列就是队列中的元素具有单调性的队列。

2、单调队列模板

（1）问题

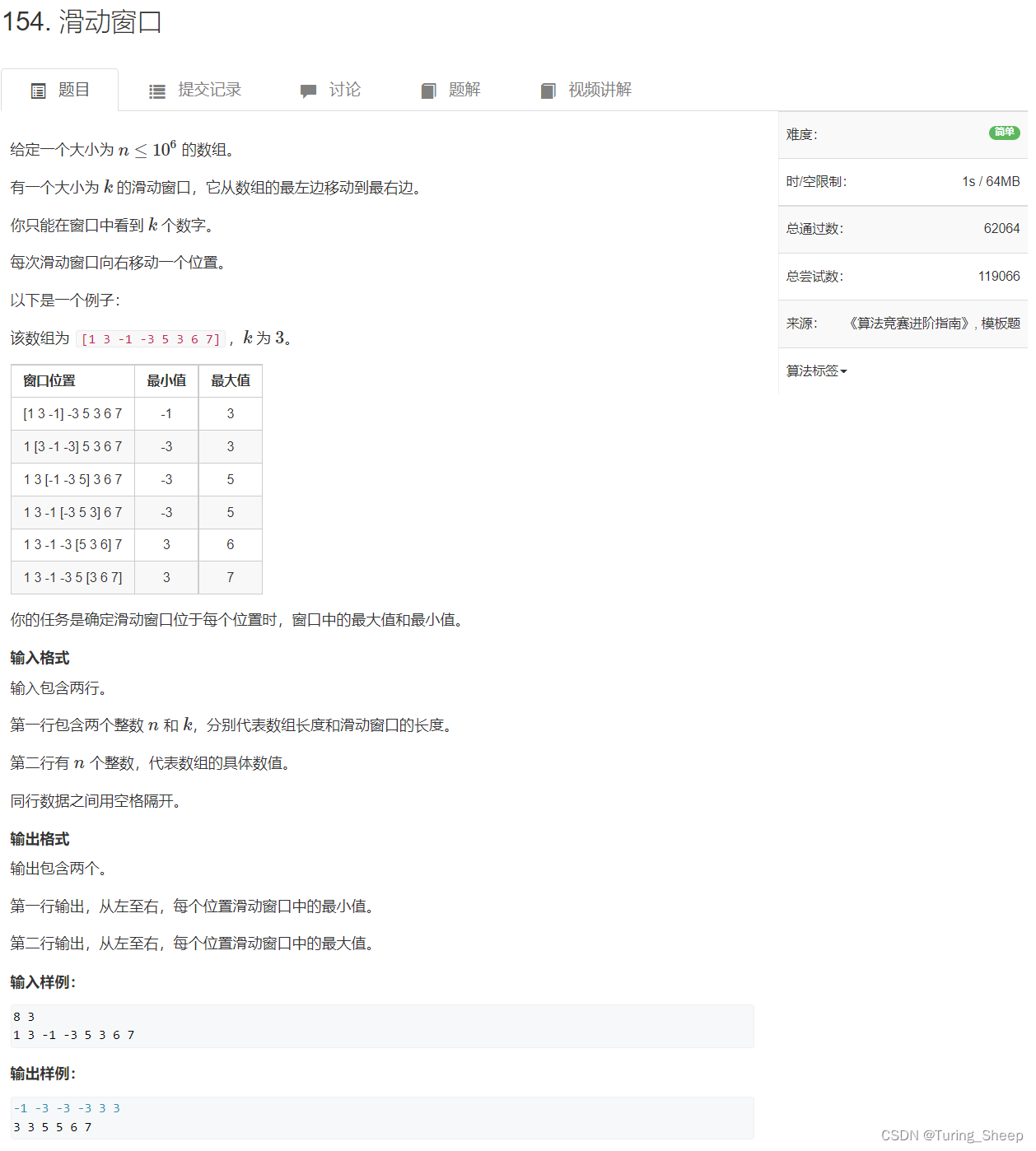
（2）分析

我们以最小值为例：

这道题我们同样可以采用暴力的做法：两个for循环相互嵌套。我们发现这种情况的时间复杂度是O(N²)。很明显，这种算法是非常低效的。

那么我们换一种算法：

我们先来思考一下，这道题适合什么样的数据结构？不难发现，这个滑动窗口是从前向后移动，即先进先出。所以我们想到了队列这种数据结构来存储。

那么队列是在队头输出的，因此我们需要保证队头输出的数据是最小值。此时受到刚才单调栈的影响，我们很容易想到这里应该是构造一个单调递增的队列，这样我们就能够保证队列中的第一个元素是最小的。

此时大家就会有一个疑问，为什么必须单调呢？我们明明只需要保证第一个最小即可。那么我们假设第一个是最小的，第二个是最大的。当我们的第一个元素滑出窗口的时候，第二个元素成为了第一个元素，此时第一个元素就不再是最小的。因此，我们保证单调性的时候，就能够保证每个元素做队头的时候，都小于后续的元素。

我们如何实现呢？单调递增的特点就是前一个元素小于该元素。接着我们就能写出下列的步骤：

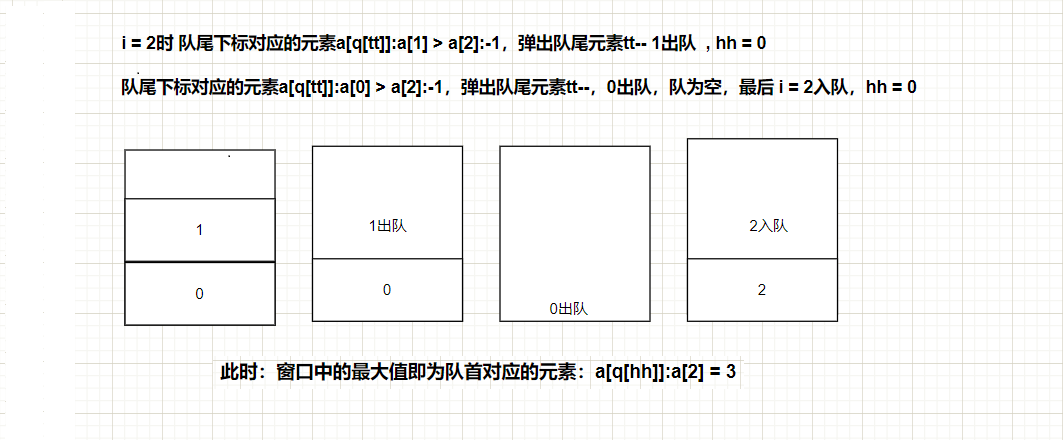
• step1 : 在队列不为空的条件下，判断第一个元素是否在窗口内。
• step2 : 若队尾元素大于等于目标元素则删除
• step3 ：目标元素进队。

在进行步骤1的判断的时候，我们需要一个计数器去记录，但是这样是相当麻烦的，因此我们将下标存储到队列中，这样的话，我们就能够通过下标的方式去判断队头是否出队。

我们还是解决一下几个问题：
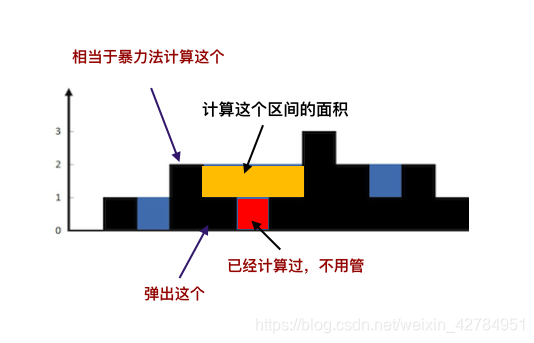
为什么要不满足单调性的元素可以删除？

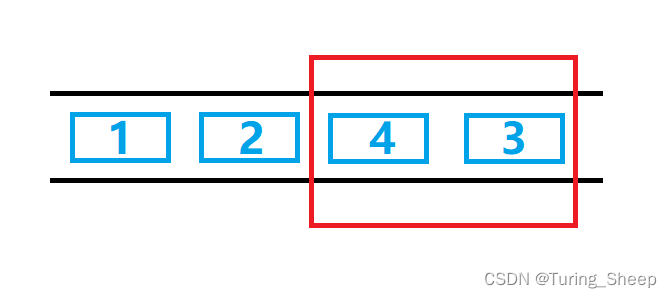
在这个队列中，只要有3的存在，4必不可能是答案，那么当3不存在的时候呢？那么4更不可能是答案了，因为我们是在队头删除元素的。所以3出队的前提是4出队。因此只有4没有3的情况是不存在的。所以我们可以删除。

那么为什么目标元素一定要进队呢？
因为经过单调性的处理，目标元素就成了队中最大的，虽然目标元素队前的元素比其要小，但是他们都是先出队的，所以当前面的元素都出队的时候，该目标元素有可能成为答案，所以我们要让每个目标元素的下标都进队。

#include<iostream>
using namespace std;
const int N=1000010;
int a[N],q[N],h,t;
int main()
{int n,k;cin>>n>>k;for(int i=0;i<n;i++){scanf("%d",a+i);if(h<=t&&q[h]<i-k+1)h++;while(h<=t&&a[q[t]]>=a[i])t--;q[++t]=i;if(i-k+1>=0)printf("%d ",a[q[h]]);}puts("");h=0,t=-1;for(int i=0;i<n;i++){if(h<=t&&q[h]<i-k+1)h++;while(h<=t&&a[q[t]]<=a[i])t--;q[++t]=i;if(i-k+1>=0)printf("%d ",a[q[h]]);}return 0;
}

我们发现，判断单调性的时候，我们是在队尾删除，判断是否在窗口内的时候，是在队头删除的。所以这不是普通的队列，而是双端队列，即STL中的deque。所以我们可以通过deque容器来实现。

#include<iostream>
#include<deque>
#include<vector>
using namespace std;
int main()
{int n,k,b;cin>>n>>k;vector<int>a;deque<int>q;for(int i=0;i<n;i++){scanf("%d",&b);a.push_back(b);if(!q.empty()&&q.front()<i-k+1)q.pop_front();while(!q.empty()&&a[q.back()]>=a[i])q.pop_back();q.push_back(i);if(i-k+1>=0)printf("%d ",a[q.front()]);}puts("");q.clear();for(int i=0;i<n;i++){if(!q.empty()&&q.front()<i-k+1)q.pop_front();while(!q.empty()&&a[q.back()]<=a[i])q.pop_back();q.push_back(i);if(i-k+1>=0)printf("%d ",a[q.front()]);}return 0;
}