单调栈和单调队列

本文摘自博客，欢迎前往博客以获得更好的体验。

单调栈

从名字上就听的出来，单调栈中存放的数据应该是严格单调有序的，具有以下两个性质。

满足从栈顶到栈底的元素具有严格的单调递增或单调递减性；
满足栈的后进先出特性，即越靠近栈底的元素越早进栈。

单调栈也分为单调递增栈和单调递减栈。

单调递增栈：单调递增栈就是从栈底到栈顶数据是从小到大
单调递减栈：单调递减栈就是从栈底到栈顶数据是从大到小

伪代码

stack<int> st;
for (遍历这个数组){if (栈空 || 栈顶元素大于等于当前比较元素){入栈;}else{while (栈不为空 && 栈顶元素小于当前元素){栈顶元素出栈;更新结果;}当前数据入栈;}
}

单调栈的维护

如何维护一个单调栈？出栈很简单，与普通栈相同，关键操作是入栈。

具体进栈过程

对于单调递增栈，若当前进栈元素为e，从栈顶开始遍历元素，把小于e或者等于e的元素弹出栈，直接遇到一个大于e的元素或者栈为空为止，然后再把e压入栈中。
对于单调递减栈，则每次弹出的是大于e或者等于e的元素。

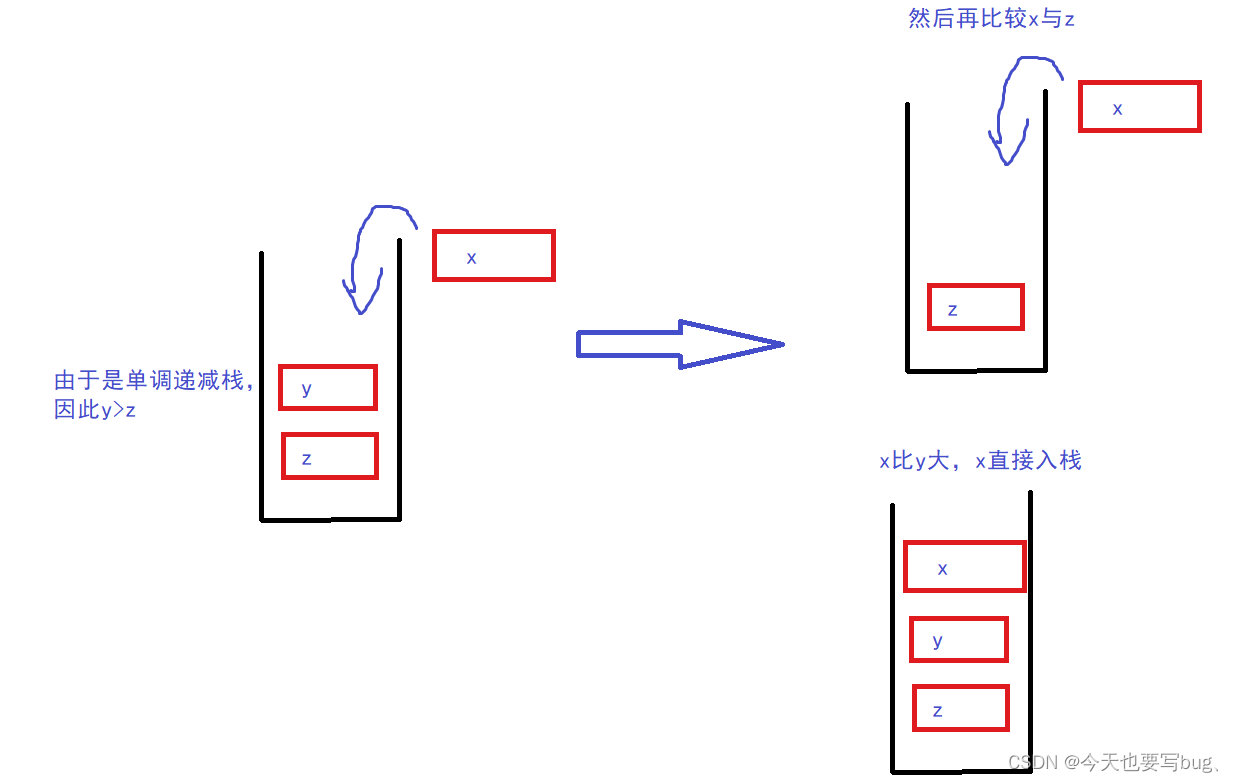
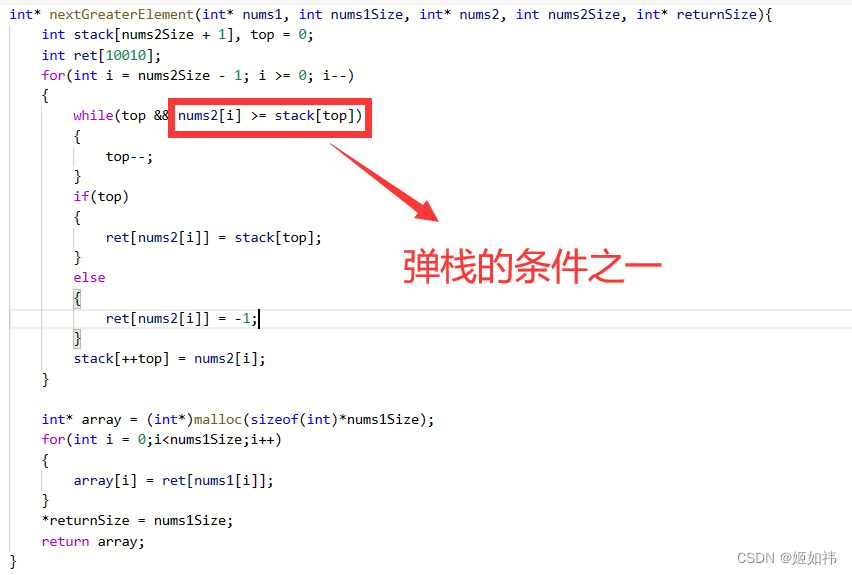
对于一个元素a，如果栈空则直接入栈。否则比较a与栈顶元素。假设一个单调递增的栈，若a > 栈顶元素，则直接把a入栈，栈仍满足单调的性质。若a < 栈顶元素，则将栈顶元素出栈，直到满足a < 栈顶元素，此时将a入栈。

例子

进栈元素分别为3，4，2，6，4，5，2，3

例题

同样，C++在实现时，我们也可以使用STL中的栈。

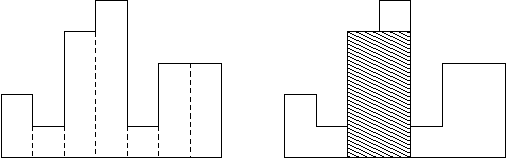
柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

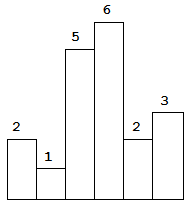
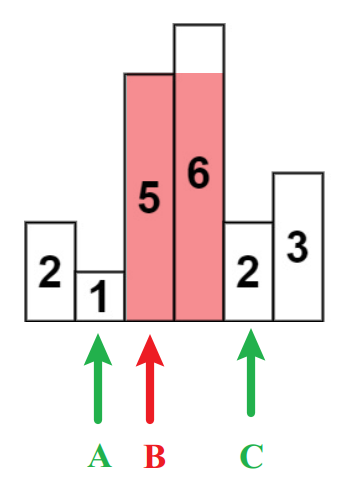
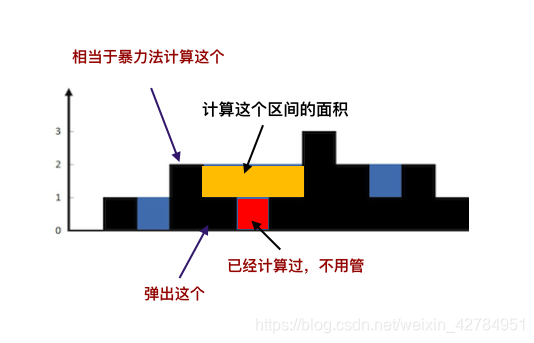
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 $[2, 1, 5, 6, 2, 3]$ 。

图中阴影部分为所能勾勒出的最大矩形面积，其面积为 $10$ 个单位。

思路：

初看此题，第一个想到的就是暴力遍历。而暴力遍历又分两种情况，即枚举宽与枚举高。
枚举宽时，我们使用两重循环枚举矩形的左右边界以固定宽度 w ，时间复杂度为 $O(N^2)$ 。
枚举高时，我们可以使用一重循环枚举某一根柱子，将其固定为矩形的高度 h。随后我们从这跟柱子开始向两侧延伸，直到遇到高度小于 h 的柱子，就确定了矩形的左右边界。时间复杂度也为 $O(N^2)$ 。
很容易发现，枚举宽的做法已经使用了双重循环，很难再优化。所以我们通过对枚举高这一做法进行优化。

那么，该如何去寻找左右边界值呢？

这时，我们便可以使用单调栈进行优化。

在思路中，我们枚举高说向左右遍历寻找。未来降低时间复杂度，我们可以使用单调栈只向一边遍历。

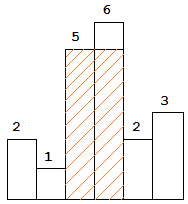
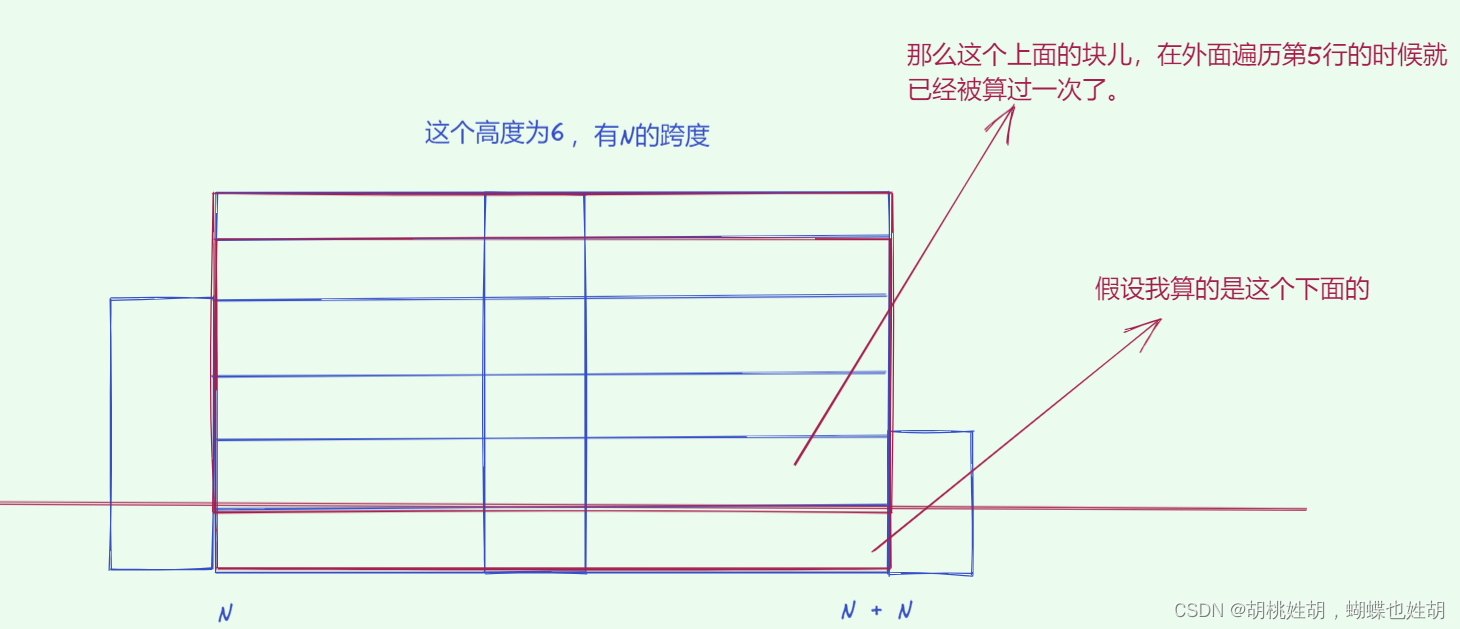
当第i个柱子进栈时，如果栈顶的高度低于或等于第i个柱子，则第i个柱子进栈；

如果栈顶的高度高于第i个柱子，则出栈，并计算以柱子A为高的矩形最大面积。

同时，为防止越界问题，我们可以在左右两侧虚拟两根无限低的柱子，记高度为 $0$ 。

int largestRectangleArea(int* heights, int heightsSize){int top = -1;int area, i;int maxarea = 0;int *stack = (int *)malloc(sizeof(int) * (heightsSize + 2));int *buff = (int *)malloc(sizeof(int) * (heightsSize + 2));buff[0] = 0;for (int i = 1; i <= heightsSize; i++) {buff[i] = heights[i - 1];}buff[heightsSize + 1] = 0;stack[++top] = 0;for (i = 1; i < heightsSize + 2; i++) {while (top > 0 && buff[i] < buff[stack[top]]) {area = (i - stack[top - 1] - 1) * buff[stack[top]];maxarea = maxarea > area ? maxarea : area;top--;}stack[++top] = i;}return maxarea;
}

C++

int largestRectangleArea(vector<int>& heights) {int n = heights.size();vector<int> left(n), right(n, n);stack<int> mono_stack;for (int i = 0; i < n; ++i) {while (!mono_stack.empty() && heights[mono_stack.top()] >= heights[i]) {right[mono_stack.top()] = i;mono_stack.pop();}left[i] = (mono_stack.empty() ? -1 : mono_stack.top());mono_stack.push(i);}int ans = 0;for (int i = 0; i < n; ++i) {ans = ans > ((right[i] - left[i] - 1) * heights[i]) ? ans : ((right[i] - left[i] - 1) * heights[i]);}return ans;
}

单调队列

队列中元素之间的关系具有严格单调有序性，而且，队首和队尾都可以进行出队操作，只有队尾可以进行入队操作。因此，在单调队列中求最值十分容易。

单调队列与普通队列有些不同，因为右端既可以插入又可以删除，因此在代码中通常用一份数组和 $r e a r$ 与 $r e a r$ 两个指针来实现，而不是使用 STL 中的 $q u e u e$ 。如果一定要使用 STL ，那么则可以使用双端队列（即两端都可以插入和删除），即 $d e q u e$ 。

队列的大小问题

在谈及单调栈时，无需关心栈的大小。而对于队列，队列的大小就很重要了。如果队列满了，我们的解决方法是，将队列头的元素弹出，再添加新的元素到队列尾。

单调队列的维护

具体入队过程

对于单调递增队列，设当前准备入队的元素为e，从队尾开始把队列中的元素逐个与e对比，把比e大或者与e相等的元素逐个删除，直到遇到一个比e小的元素或者队列为空为止，然后把当前元素e插入到队尾。
对于单调递减队列也是同样道理，只不过从队尾删除的是比e小或者与e相等的元素。

例子

队列大小不能超过3，入队元素依次为3，2，8，4，5，7，6，4

例题

滑动窗口

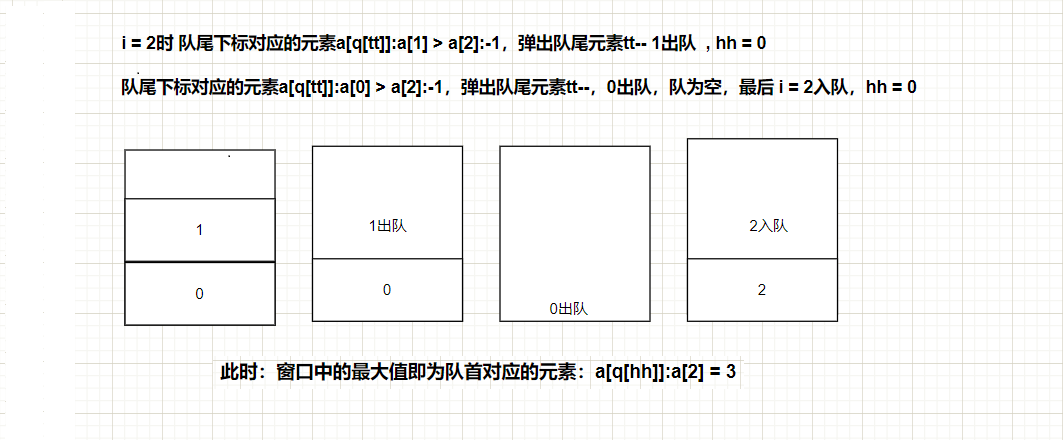
给定一个数列，从左至右输出每个长度为 $m$ 的数列段内的最小数和最大数。

Window position	Minimum value	Maximum value
[1 3 -1] -3 5 3 6 7	-1	3
1 [3 -1 -3] 5 3 6 7	-3	3
1 3 [-1 -3 5] 3 6 7	-3	5
1 3 -1 [-3 5 3] 6 7	-3	5
1 3 -1 -3 [5 3 6] 7	3	6
1 3 -1 -3 5 [3 6 7]	3	7

数列长度： $N <= 10^6$ ， $m < = N$

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1e6+5;
int n, k, a[maxn];
int q[maxn];//队列，存的是下标
int main(){scanf("%d%d",&n,&k);for(int i = 1; i <= n; ++i) scanf("%d",&a[i]);//维护最小值，序列要单调递增int front = 1, rear = 0;for(int i = 1; i <= n; ++i){//如果如果尾部的在滑块之外，则删掉他们while(front <= rear && q[front]+k <= i) ++front;//如果头部的比当前的大，那么a[i]从头进去，队列就不递增了，所以删掉比a[i]大的头部while(front <= rear && a[i] < a[q[rear]]) --rear;q[++rear] = i;//头部插入iif(i >= k) printf("%d ", a[q[front]]);//因为单调递增，所以答案在a的下标就是q[front]}//维护最大值，同上putchar('\n');memset(q,0,sizeof(q));front = 1, rear = 0;for(int i = 1; i <= n; ++i){while(front <= rear && q[front]+k <= i) ++front;while(front <= rear && a[i] > a[q[rear]]) --rear;q[++rear] = i;if(i >= k) printf("%d ", a[q[front]]);}return 0;
}