这里是我的blog：有更多算法分享。排版可能也会更好看一点=v=
https://endlesslethe.com/monotone-queue-and-stack-tutorial.html

前言

单调栈和单调队列算是栈和队列的高级应用吧，在公司面试中应该是不怎么会出现的（除非算法岗？）。
因为原理比较简单，网络上的相关资料反而对于这两个东西说得都不甚清楚，尤其是它们的应用方法。最基本的两本中文算法书“紫书”和“白皮”都没有提到。

而我因为平日要做的事情也很多，仓促中写下的这篇文章难免表达上会有不清晰的地方和各种疏漏，希望读者不吝赐教=v=。

栈和队列这两种基础数据结构戳：TBC。

先说明一下，无论是栈还是队列，我们把元素进入的一端称作“尾部”，并用双引号标出，另一端称作“尾部”。对于栈，头部即是栈底，尾部即是栈顶。对于队列，头部对应队首，尾部对应队尾。

注：我不确定单调队列是否翻译成monotone queue，算法导论上没有提到这个数据结构，Bing上也没有搜索到对应它的结果（倒是返回了关于优先队列的结果）。

单调栈

我们都已经非常熟悉栈了，它具有先入后出的性质。而单调栈为了满足单调的要求，增加了一个性质：

• 从栈顶到栈底的元素是严格递增（or递减）

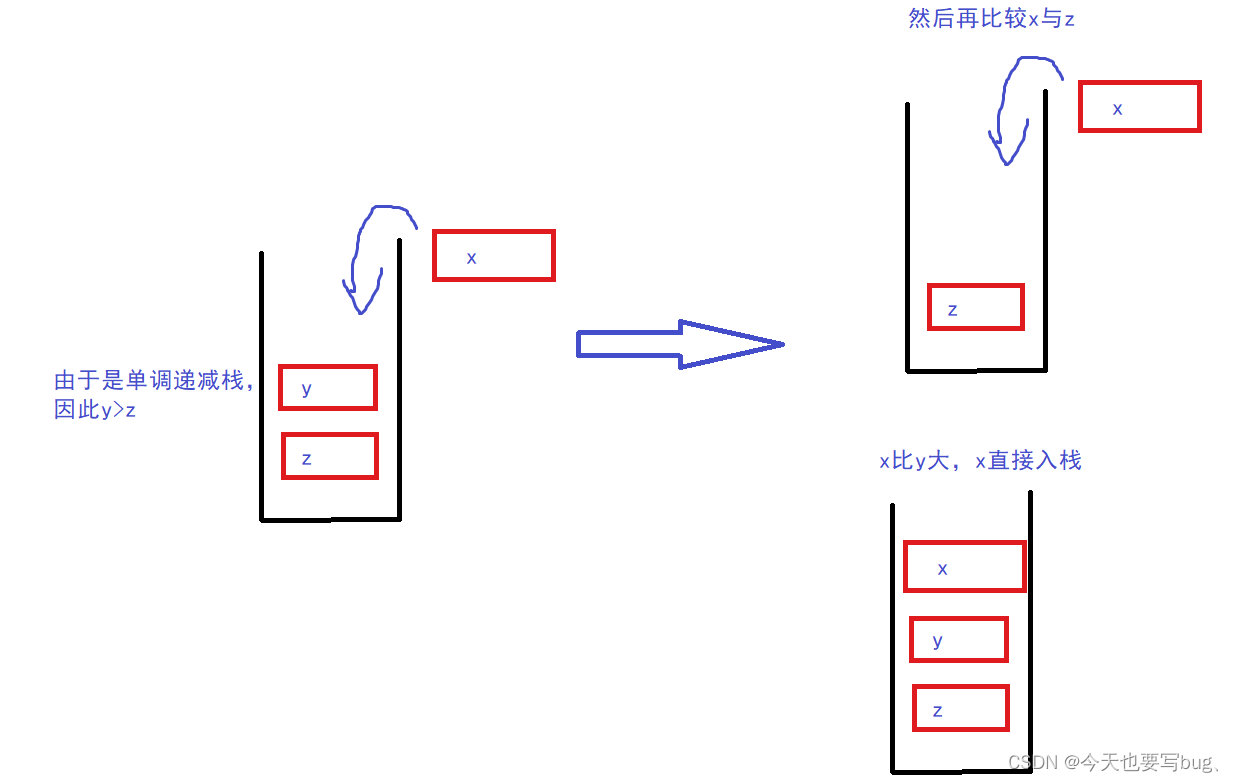
显然，这和我们的正常的流程有一定矛盾之处——如果栈中是5 4 3 2 1，如果压入3怎么办？
原来我们只需要添加到栈尾即可，现在则需要将3 2 1弹出，再压入3，栈变成5 4 3
注：弹出的元素我们直接舍弃掉。

具体进栈过程

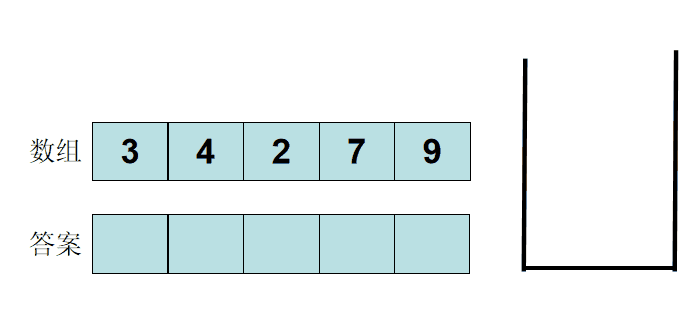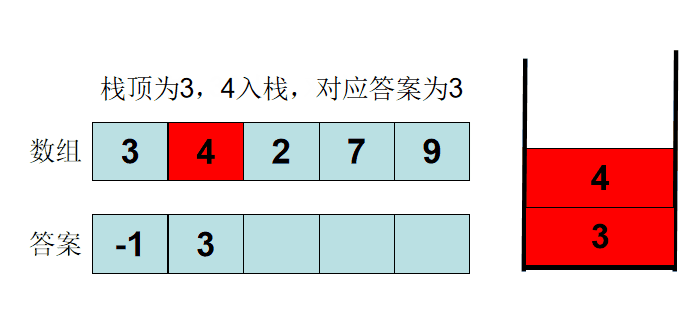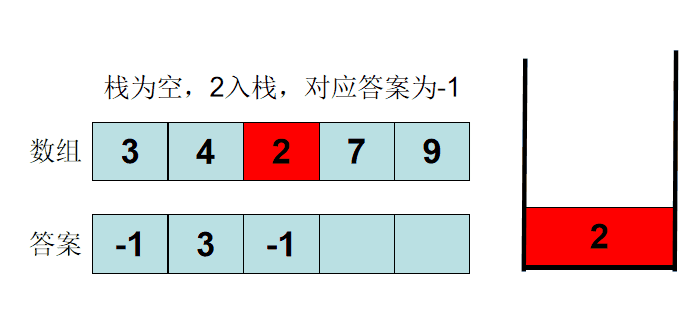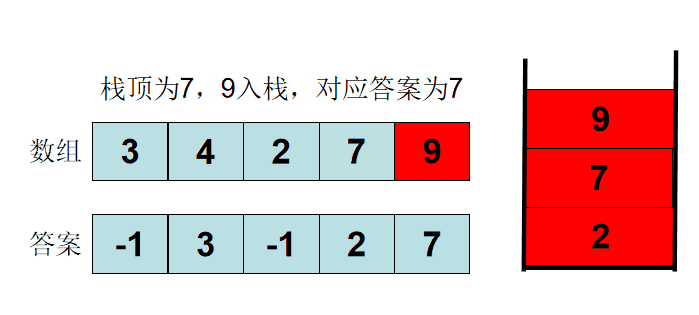
• 对于单调递增栈，若当前进栈元素为e，从栈顶开始遍历元素，把小于e或者等于e的元素弹出栈，直接遇到一个大于e的元素或者栈为空为止，然后再把e压入栈中。
• 对于单调递减栈，则每次弹出的是大于e或者等于e的元素。

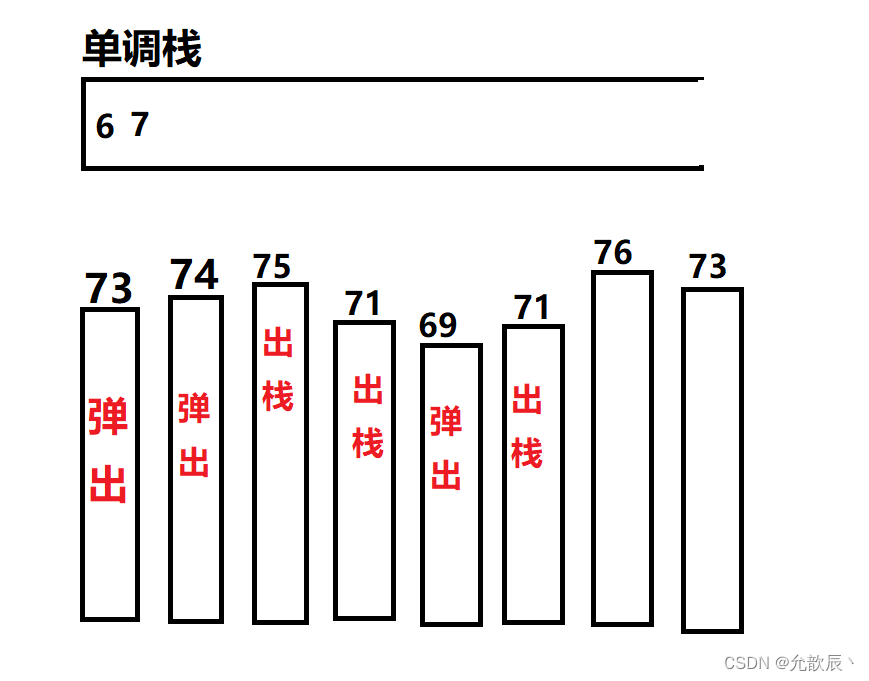
一个单调递增栈的例子：

进栈元素分别为3，4，2，6，4，5，2，3

第i步	操作	结果
1	3进栈	3
2	3出栈，4进栈	4
3	2进栈	4 2
4	2、4出栈，6进栈	6
5	4进栈	6 4
6	4出栈，5进栈	6 5
7	2进栈	6 5 2
8	2出栈，3进栈	6 5 3

这里提供一个递增的单调栈的图，元素依次为3，2，8，4，5，7，6，4
注意看随着i的变化，栈中元素的变化。

单调队列

对于单调队列，从单调栈的性质我们可以类推出：

• 从队列头到队列尾的元素是严格递增

添加元素e到队尾时，我们采取的解决方法同样是，先从队尾删去小于等于e的元素。
注意，普通的队列queue是不支持从队尾删除的，我们需要使用双端队列deque，即有两个指针，一头一尾。

队列的大小问题

在谈及单调栈时，我略去了栈的大小这一个问题，因为在实际使用中（比如函数调用栈）栈就通常没有大小的概念。而对于队列，它的大小就很重要了。
如果队列满了，我们的解决方法是，将队列头的元素弹出，再添加新的元素到队列尾。

具体入队过程

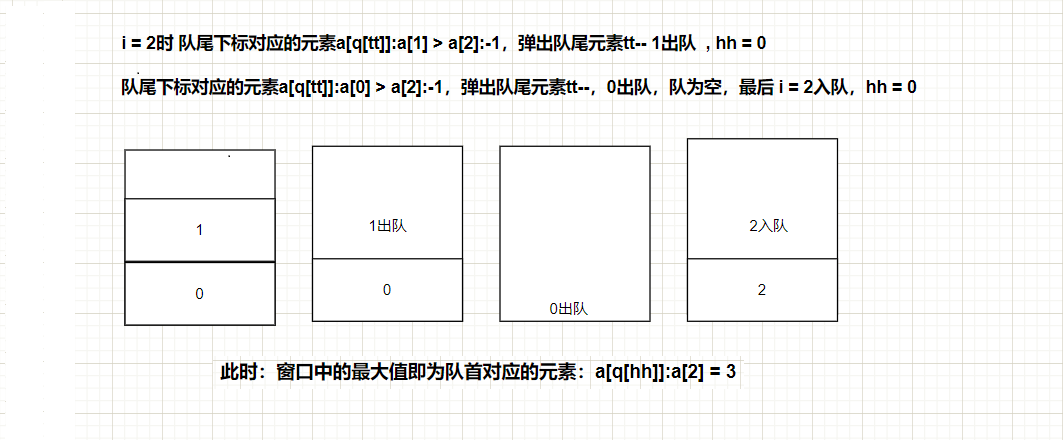
• 对于单调递增队列，设当前准备入队的元素为e，从队尾开始把队列中的元素逐个与e对比，把比e大或者与e相等的元素逐个删除，直到遇到一个比e小的元素或者队列为空为止，然后把当前元素e插入到队尾。
• 对于单调递减队列也是同样道理，只不过从队尾删除的是比e小或者与e相等的元素。

一个递增单调队列的例子

队列大小不能超过3，入队元素依次为3，2，8，4，5，7，6，4

第i步	操作	结果
1	3入队	3
2	3从队尾出队，2入队	2
3	8入队	2 8
4	8从队尾出队，4入队	2 4
5	5入队	2 4 5
6	2从队头出队，7入队	4 5 7
7	7从队尾出队，6入队	4 5 6
8	6、5、4从队尾出队，4入队	4

单调队列和单调栈的区别和联系

单调队列和单调栈的相同点

• 单调队列和单调栈的“头部”都是最先添加的元素，“尾部”都是最后添加的元素。
• 递增和递减的判断依据是：从栈底（队尾）到栈顶（队首），元素大小的变化情况。所以队列和栈是相反的。
• 它们的操作是非常相似的。当队列长度为无穷大时，递增的单调队列和递减的单调栈，排列是一样的！
  原因在于，长度为无穷大的的队列不会在“头部”有popfront操作，而在“尾部”的操作是一模一样的：数据都从“尾部”进入，并按照相同的规则进行比较。
• 两者维护的时间复杂度都是O(n)，因为每个元素都只操作一次。

区别

• 队列可以从队列头弹出元素，可以方便地根据入队的时间顺序（访问的顺序）删除元素。
• 这样导致了单调队列和单调栈维护的区间不同。当访问到第i个元素时，单调栈维护的区间为[0, i)，而单调队列维护的区间为(lastpop, i)
• 单调队列可以访问“头部”和“尾部”，而单调栈只能访问栈顶（也就是“尾部”）。这导致单调栈无法获取[0, i)的区间最大值/最小值。

综上所述，单调队列实际上是单调栈的的升级版。单调栈只支持访问尾部，而单调队列两端都可以。当然，单调栈的编程上（两个函数）比单调队列（三个函数）要简单。

单调队列和单调栈的性质

下面的总结，如果没有特别指出是单调队列/单调栈，那么就不区分队列和栈，而且从“头部”到“尾部”数据是严格递减的，请读者自行注意。

1. 具有单调性
2. 容器中的元素个数永远不为空。（因为当添加一个元素时，它要么直接被添加到“尾部”，要么弹出k个比它小的数后再被添加到“尾部”）
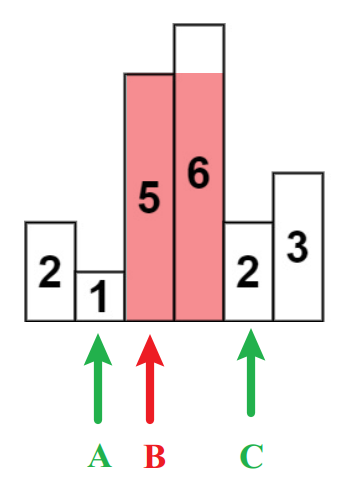
3. 对于一个元素i，我们可以知道在它左边区间，第一个比它小的值，也就是\({\rm{Max({ v[x]|x < i \& \& v[x] < v[i]} )}}\)
   在元素添加的过程中，我们会不断弹出比它小的值，最后一个弹出的值，即为所求。如果没有元素被弹出，那就无法求出，虽然这个数一定存在。
   顺便在这里多提一句，第二个比它小的数是一定不知道的，因为不确定是否被弹出
4. 对于一个元素i，我们可以知道在它左边区间，第一个比它大的值，也就是\(Min\left( {{ v\left[ x \right]|x < i\& \& v\left[ x \right] > v\left[ i \right]} } \right)\)
   在弹出比i小的所有元素后，栈顶的元素即为所求。如果栈为空，也无法求出。
5. 根据2和3，它们是元素插入时所获得的信息，我们可以推出当元素被弹出时能获得的信息：在右边区间，第一个比它大的值。
6. 我们可以统计在添加元素过程中，弹出了多少个元素。

注：这里的大于和小于并不严谨，是为了表述尽量简单。请读者自己注意大于/大于等于，小于/小于等于。根据原则：容器中等于e的元素也会被弹出，进行判断即可。

单调队列和单调栈的应用

单调队列

• 可以查询区间最值（不能维护区间k大，因为队列中很有可能没有k个元素）
• 优化DP（见参考文献3）
  单调队列一般是用于优化动态规划方面问题的一种特殊数据结构，且多数情况是与定长连续子区间问题相关联。

单调栈即可完成的

对于某个元素i：

• 左边区间第一个比它小的数，第一个比它大的数
• 确定这个元素是否是区间最值
• 右边区间第一个大于它的值
• 到 右边区间第一个大于它的值 的距离
• 确定以该元素为最值的最长区间

在具体题目里，如何使用单调栈和单调队列是一目了然的，不要强迫自己记忆，而是要理解
要想掌握好单调栈和单调队列，必须要做一些题

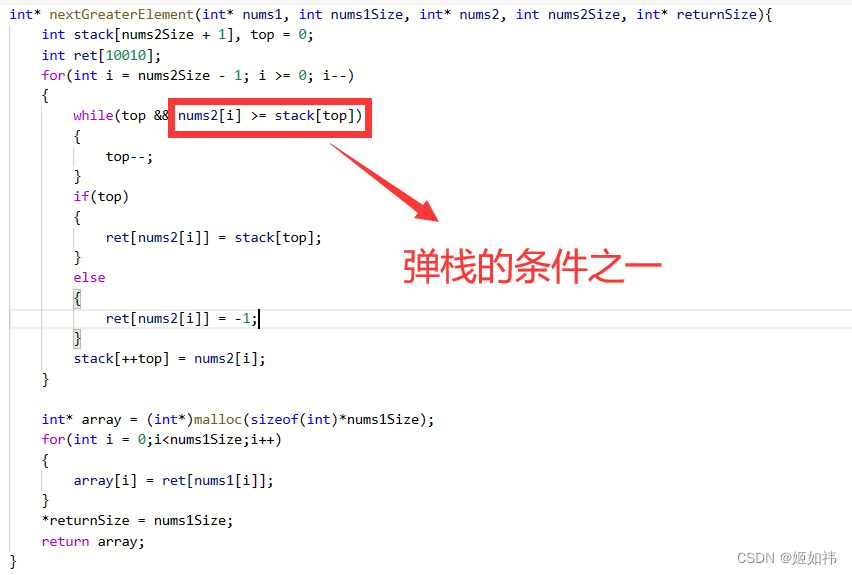
具体代码

单调队列

//在“尾部”添加元素x
while (l != r && mq[r] <= x) r--;
mq[++r] = x;//查询队首元素
if (l != r) printf("%d\n", mq[l+1]);
else printf("-1\n");//弹出队首元素
if (l != r) l++;

单调栈

//在“尾部”添加元素
while (r != 0 || ms[r] <= x) r--;
ms[++r] = x;//查询栈顶元素
if (r != 0) printf("%d\n", ms[r]);
else printf("-1");

注：在前面的情况，我们是直接压入了元素e。但我们往往选择压入元素e的index（依据题型来决定），需要稍作修改，这里不提供对应代码。

题目总结

• FZU 1894
  1.C name rp 名字为name人品为rp的人排到队尾
  2.G 队首的人出队
  3.Q 询问当前队列中rp最高的
  实现这三个操作。模板题。
  AC代码
• POJ 2796
  最大化(区间min * 区间和)
  使用单调栈，从某一元素i向左右区间延伸，找到最大区间。
  AC代码
• HDU 5033
  模板题
• FJSDFZOJ 1308 音乐会的等待/诺诺的队列
  对于l和r，如果[l, r]内没有大于min(l,r)的数，则这两个数可以互相看见。
  求能互相看见的对数
  标程对题意的理解比较奇怪。
  AC代码

参考文献

I. 单调队列 单调栈总结
II. 单调栈的介绍以及一些基本性质
III. 单调队列，单调栈总结
IV. 单调队列或单调栈的学习及认识