定义：

	单调栈，顾名思义就是栈内元素单调按照递增(递减)顺序排列的栈。

单调递增栈：

①在一个队列中针对每一个元素从它右边寻找第一个比它小的元素

②在一个队列中针对每一个元素从它左边寻找第一个比它小的元素

单调递减栈：

①在一个队列中针对每一个元素从它右边寻找第一个比它大的元素

②在一个队列中针对每一个元素从它左边寻找第一个比它大的元素

单调栈何时用：为任意一个元素找左边和右边第一个比自己大/小的位置用单调栈.

由于每个元素最多各自进出栈一次,复杂度是O(n).

单调递增栈用于找到当前元素左边第一个小于它的的元素

单调递增栈模板：

#include<iostream>
#include<stack>
using namespace std;
int main()
{int n;cin>>n;stack<int>st;for(int i=1;i<=n;i++){int x;cin>>x;while(!st.empty()&&st.top()>x)st.pop();cout<<(st.empty()?-1:st.top())<<endl;st.push(x);}return 0;} 

POJ - 2559    直方图中最大的矩形

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为 2,1,4,5,1,3,32,1,4,5,1,3,3 的矩形组成的直方图，矩形的宽度都为 11：

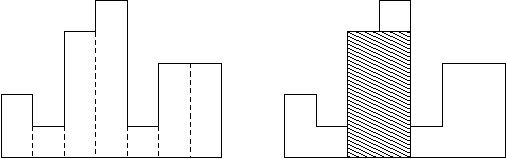
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数 nn 开始，表示组成直方图的矩形数目。

然后跟随 n 个整数 h1，…，hn。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为 1。

同行数字用空格隔开。

当输入用例为 n=0 时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

1≤n≤100000,
0≤hi≤1000000000

输入样例：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

8
4000

#include<iostream>
#include<stack>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=1e5+5;
int n;
int l[N],r[N];
typedef pair<int,int>P;
P p[N];
int main()
{while(cin>>n&&n){stack<P>st;for(int i=1;i<=n;i++){int x,ind;cin>>x;p[i].first=x;  p[i].second=i;ind=i-1;while(!st.empty()&&st.top().first>=p[i].first)st.pop(),ind--;
//			cout<<(st.empty()?-1:st.top())<<" ";if(st.empty())l[i]=-1;else {P pp=st.top();l[i]=pp.second;}st.push(p[i]);}while(!st.empty())st.pop();for(int i=n;i>=1;i--){int ind;ind=i+1;while(!st.empty()&&st.top().first>=p[i].first)st.pop(),ind++;if(st.empty())r[i]=-1;else{P pr=st.top();r[i]=pr.second;}st.push(p[i]);}long long maxx=-1;for(int i=1;i<=n;i++){int ll,rr;if(l[i]==-1)ll=0;else ll=l[i];if(r[i]==-1)rr=n+1;else rr=r[i];maxx=max(maxx,(long long)(abs(ll-rr)-1)*p[i].first);}cout<<maxx<<endl;}return 0;} 

输入输出样例

输入 #1复制

5
1 4 2 3 5

输出 #1复制

2 5 4 5 0

 题解一：

#include<iostream>
#include<stack>
using namespace std;
const int N=3e6+10;
int a[N];
int ans[N];stack<int>st;
int main()
{int n;cin>>n;for(int i=1;i<=n;i++)scanf("%d",&a[i]);for(int i=n;i>=1;i--){while(!st.empty()&&a[st.top()]<=a[i])st.pop();//应该是小于等于，而不是小于
//		cout<<(st.empty()?0:st.top().ind)<<" ";ans[i]=(st.empty()?0:st.top());st.push(i);}for(int i=1;i<=n;i++)printf("%d%c",ans[i],i==n?'\n':' ');return 0;} 

题解二：

#include<iostream>
#include<stack>
using namespace std;
const int N=3e6+10;
struct A{int ind,val;
}a[N];
int ans[N];
int main()
{int n;cin>>n;for(int i=1;i<=n;i++)scanf("%d",&a[i].val),a[i].ind=i;stack<A>st;for(int i=n;i>=1;i--){while(!st.empty()&&st.top().val<=a[i].val)st.pop();//注意应该是小于等于
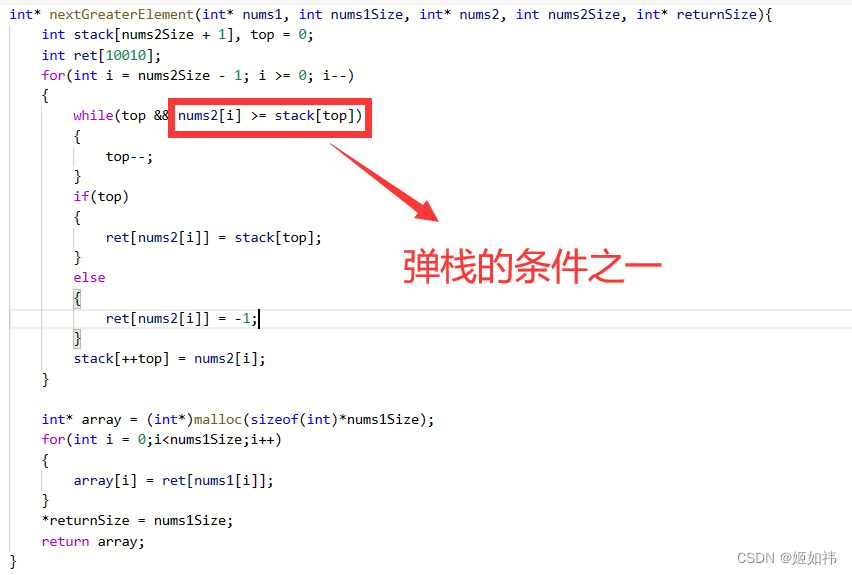
//		cout<<(st.empty()?0:st.top().ind)<<" ";ans[l++]=(st.empty()?0:st.top().ind);st.push(a[i]);}for(int i=l-1;i>=1;i--)printf("%d%c",ans[i],i==1?'\n':' ');return 0;} 

这题数据量较大，输入用cin会超时，再者找第一个大于它的数，所以用单调递减栈，只要栈顶元素小于等于入栈元素，就出栈。

接雨水

 思路：

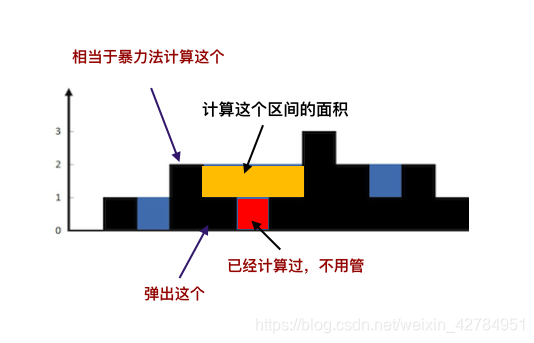
用单调递减栈，找到左边第一个比自己高的柱子。

 每当栈顶元素小于入栈元素时，将栈顶元素出栈（记作cur），然后比较此时的栈顶元素和入栈元素的大小，用小的那个减去cur就是雨水的深度，然后用下标计算出宽度，最后深度×宽度得接水量。（实现依据：单调栈里的元素具有单调性）