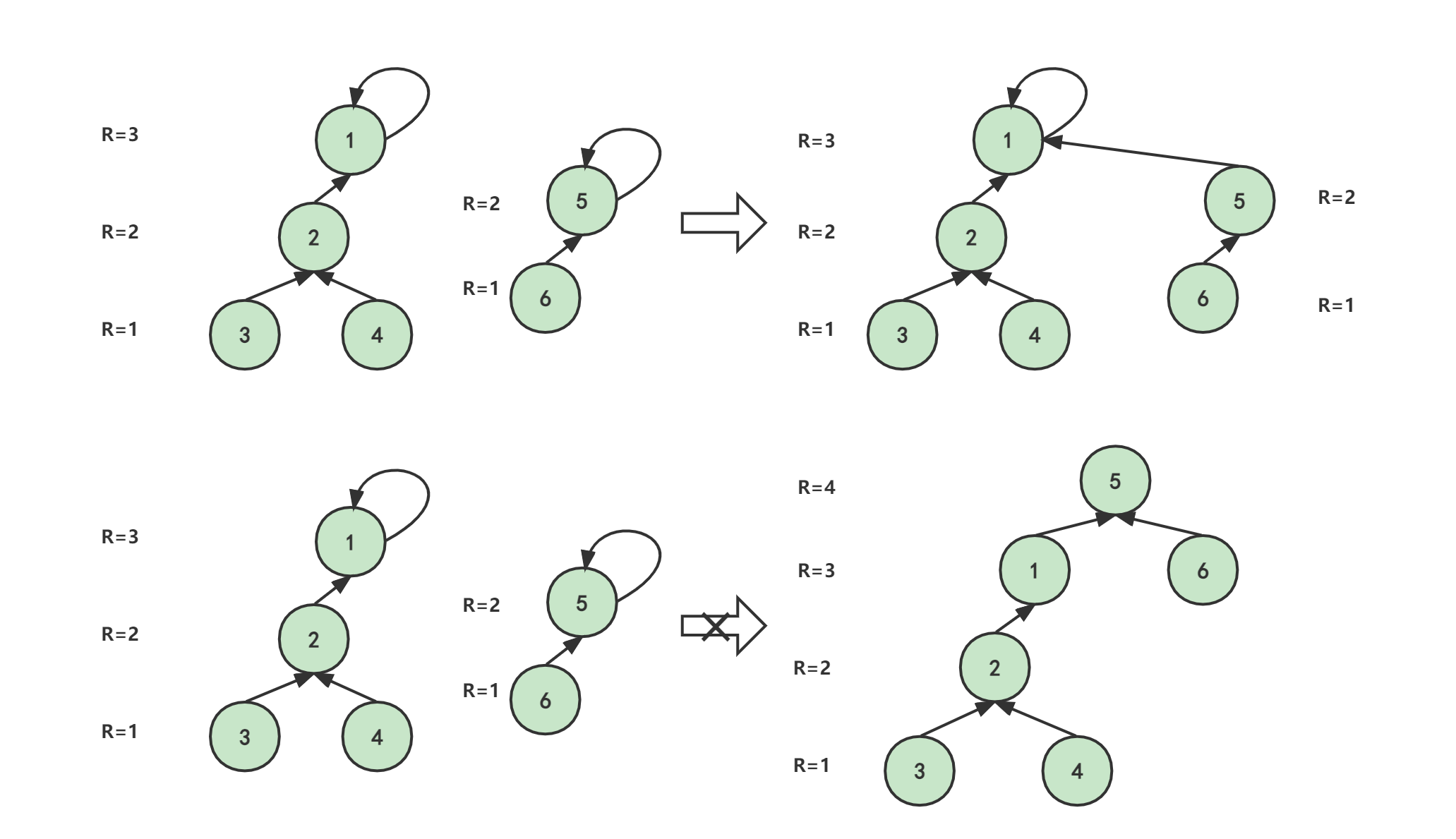
一、什么是并查集

并查集其实就是实现一个类似朋友圈的功能，朋友的朋友是朋友，朋友的朋友的朋友也是朋友，即只要有关系一些人就合并成为一个朋友圈。

并查集可以实现查询两个人是否是朋友，查询朋友圈的个数

二、并查集的原理

并查集原理和构图是类似的，但是构图每次查询的速度是 O(n) ，慢得离谱，此时查询复杂为 O(1) 的并查集算法就出现了

我们定义一个数组 f[n] ，其下标表示点，他的值表示和其它点有关系，例如 f[1] = 4，即 1 号和 4 号是朋友，如果 f[4] = 6，即说明 4 号和 6 号是朋友。

那么我们如何知道 1 号和 6 号是朋友呢？假如 f[6] = 6，那么就说明 6 的后面没有朋友了，此时我们通过 f[1] 可以找到 4 ，通过 f[4] 可以找到 6，通过 f[6] 仍然找到 6，那么这个朋友链的结尾就是6，而 f[6] = 6，仍然找到 6，那么这个朋友链的结尾也是6，那么就说明 1 号和 6 号是朋友。

我们应该能理解，我们都是通过朋友链最后一个朋友判断两个人是不是朋友的，例如：
f[1] = 4，f[4] = 6，f[6] = 9，f[9] = 5，f[5] = 5;
那么就有关系链1 — 4 — 6 — 9 — 5
无论是1、4、6、9、5中哪个数，只要顺着链往下找，最后肯定都是找到 5 的，那么我们就可以判断两个数是不是朋友

示例代码：

#include<iostream>
using namespace std;
int f[100010]; 
int find(int a){if(f[a]!=a)return find(f[a]);//如果当前节点不是末尾节点，继续往下找return a;
}
int main(){for(int i=0;i<100010;i++){//我们需要初始化f[i]的值都等于i f[i]=i;}
}

三、并查集的优化

没有优化的并查集查询的时间复杂度是O(n)，并没有达到我们想要的效果，那么我们该如何优化呢？

可以看到，一条朋友链如下
1 — 4 — 6 — 9 — 5
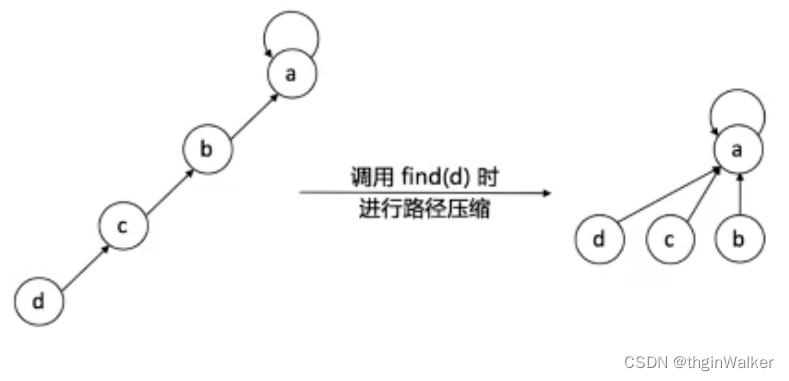
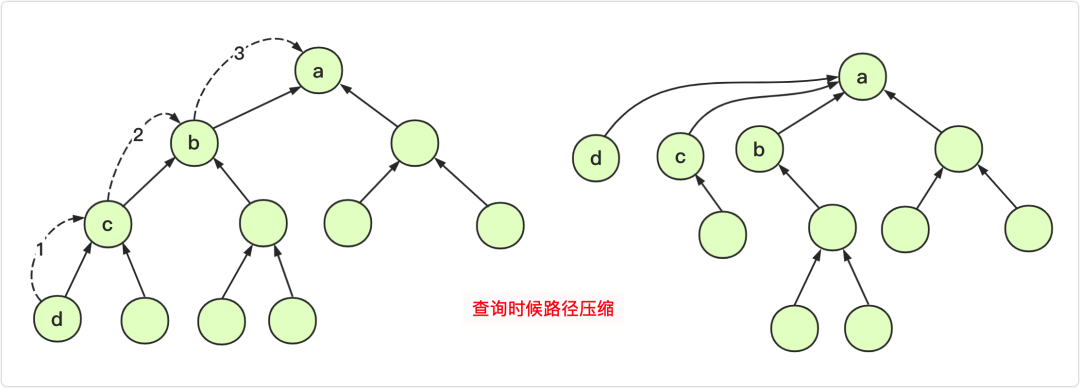
我们查找 1 时，总是要经过 4、6、9 这些没用的中间关系，我们需要尝试去掉这些冗余的查询，将关系链变为如下格式：
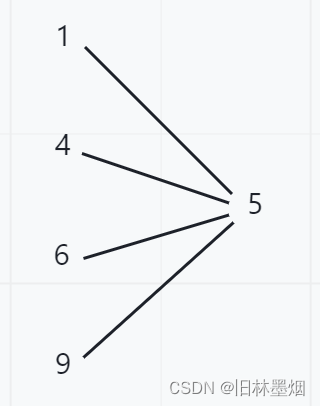
在这里插入图片描述

实际上也就是将原来的：
f[1] = 4，f[4] = 6，f[6] = 9，f[9] = 5，f[5] = 5;
转换为：
f[1] = 5，f[4] = 5，f[6] = 5，f[9] = 5，f[5] = 5;

我们只要在原来的递归查找里将查找到的值赋给当前点就好了

示例代码：

#include<iostream>
using namespace std;
int f[100010]; 
int find(int a){if(f[a]!=a)return f[a]=find(f[a]);//如果当前节点不是末尾节点，继续往下找,并且将当前点的值更新为找到的结果 return a;
}
int main(){for(int i=0;i<100010;i++){//我们需要初始化f[i]的值都等于i f[i]=i;}
}

四、并查集的基本使用

1、添加关系：f[find(a)] = find(b)
2、查询关系find(a)==find(b)，如果为真，即有关系，否则没有关系
3、查询关系集合的个数，有多少个末尾节点就有多少个集合，即 f[a]==a 的数

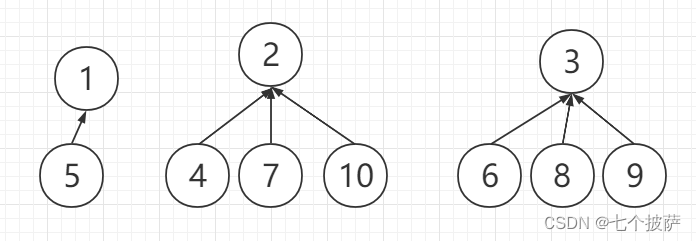
下面模拟这个图的集合：
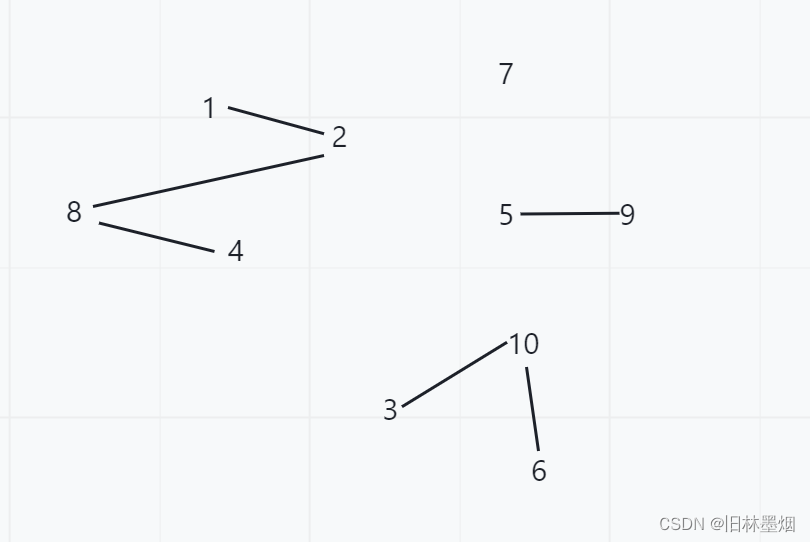
在这里插入图片描述

有边（1，2）、（2，8）、（8，4）、（5，9）、（3，10）、（10，6）

示例代码：

#include<iostream>
using namespace std;
int f[100010]; 
int find(int a){if(f[a]!=a)return f[a]=find(f[a]);//如果当前节点不是末尾节点，继续往下找,并且将当前点的值更新为找到的结果 return a;
}
int main(){for(int i=0;i<100010;i++){//我们需要初始化f[i]的值都等于i f[i]=i;}//	构造并查集 f[find(1)]=find(2);f[find(2)]=find(8);f[find(8)]=find(4);f[find(5)]=find(9);f[find(3)]=find(10);f[find(10)]=find(6);int n=0;
//	查询集合个数for(int i=1;i<=10;i++){if(f[i]==i)n++;} cout<<"有"<<n<<"个集合"<<endl; //	查询关系 int a,b;while(1){cout<<"请输入1到10的两个数："<<endl; cin>>a>>b;if(find(a)==find(b)){cout<<a<<"和"<<b<<"有关系"<<endl; }else{cout<<a<<"和"<<b<<"没有关系"<<endl; }cout<<endl;}}

运行结果：

有4个集合
请输入1到10的两个数：
2 4
2和4有关系请输入1到10的两个数：
1 5
1和5没有关系请输入1到10的两个数：
5 9
5和9有关系请输入1到10的两个数：

五、并查集模板

#include<iostream>
using namespace std;
const int N=100000;
int f[N+10]; 
int find(int a){//查询函数 if(f[a]!=a)return f[a]=find(f[a]);return a;
}void add(int a,int b){//添加关系 f[find(a)]=find(b);
}int check(int a,int b){//查询关系 return find(a)==find(b);
}int cnt(){//查询集合个数 int n=0;for(int i=1;i<=N;i++){if(f[i]==i)n++;} return n;
}void init(){//初始化 for(int i=0;i<100010;i++){f[i]=i;}
}int main(){init();}