❤️什么是并查集？

并查集是一种数据结构，用于处理一些不交集（Disjoint sets，一系列没有重复元素的集合）的合并及查询问题。

常见的两种操作：

-合并两个集合； //并

-查找某元素属于哪个集合； //查

🎶实现方法1

-用编号最小的元素标记所在的集合；

-定义一个数组 Set[1..n] ，其中 Set[i] 表示元素 i 所在的集合；

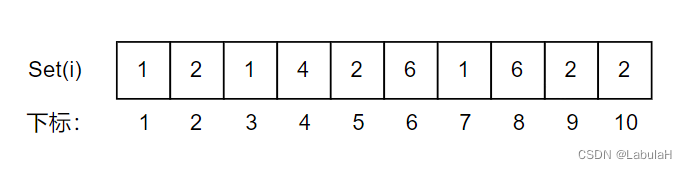
不相交集合：{1 , 3 , 7} , {4} , {2, 5, 9, 10} , {6, 8}

每个元素 i 用数组的下标表示，集合中保存的元素是集合中元素的标记。

例如：第一个不相交集合{1 , 3 , 7}，这个集合的标记为最小的元素 1，则图中Set[1]、Set[3]、Set[7]都保存这个集合的标记 1。（就相当于1是集合{1 , 3 , 7}的队长，2是集合{2, 5, 9, 10}的队长）

-查找元素：时间复杂度O(1)

find_1(x){return Set[x];
}

例如：查找元素9是哪个集合则返回Set[9]，也就是标记为2的集合。

-合并操作：时间复杂度O(N)

merge_1(a, b){i = min(a, b);j = max(a, b);for(int k=1; k<=N; k++){if(Set[k] == j)Set[k] = i;}
}

例如：合并两个集合{1 , 3 , 7} , {4}，执行merge_1(1, 4)，用两个集合的标记的较小值重新标记每个元素。

🐔实现方法2

-每个集合用树来表示；

对于数组Set[1..n]，Set[i] = i，则 i 就是队长，也就是树根；Set[i] = j，且 j != i，则 j 就是 i 的上级，也就是父节点。

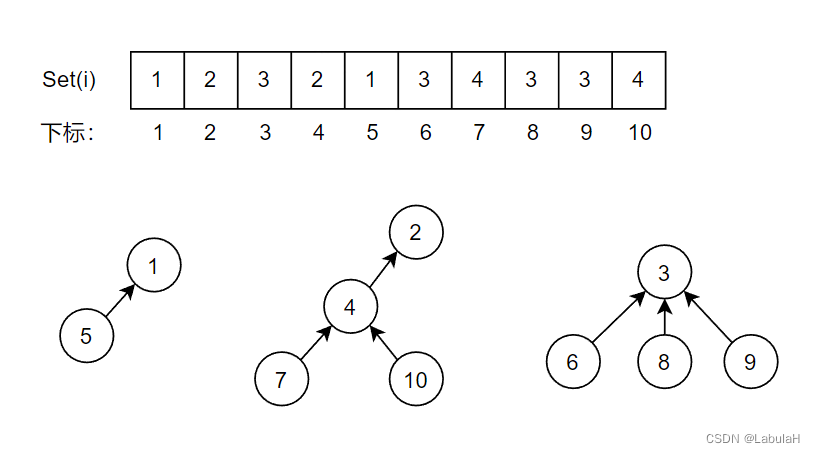
-查找元素：最坏情况的时间复杂度O(N)

find_2(x){r = x;while(Set[r]!=r)r = Set[r]; return r;
}

例如：查找元素10的大队长，10的上级是4，4的上级是，2的上级是他自己，那么2就是大队长。

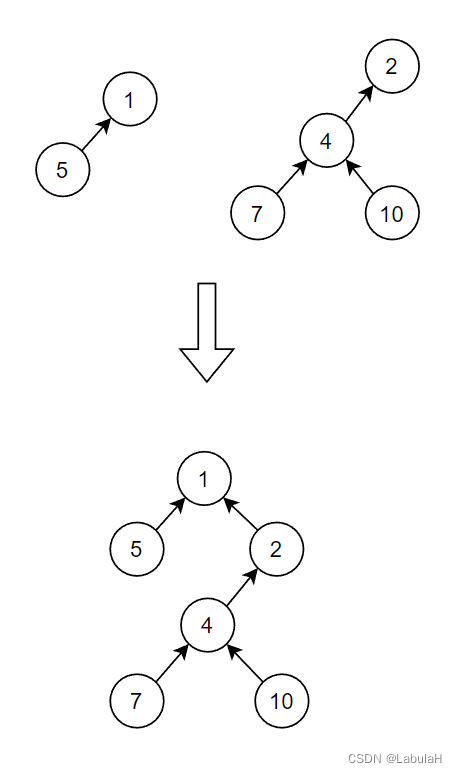
-合并操作：时间复杂度O(1)

void merge_2(a, b){Set[a] = b;
}

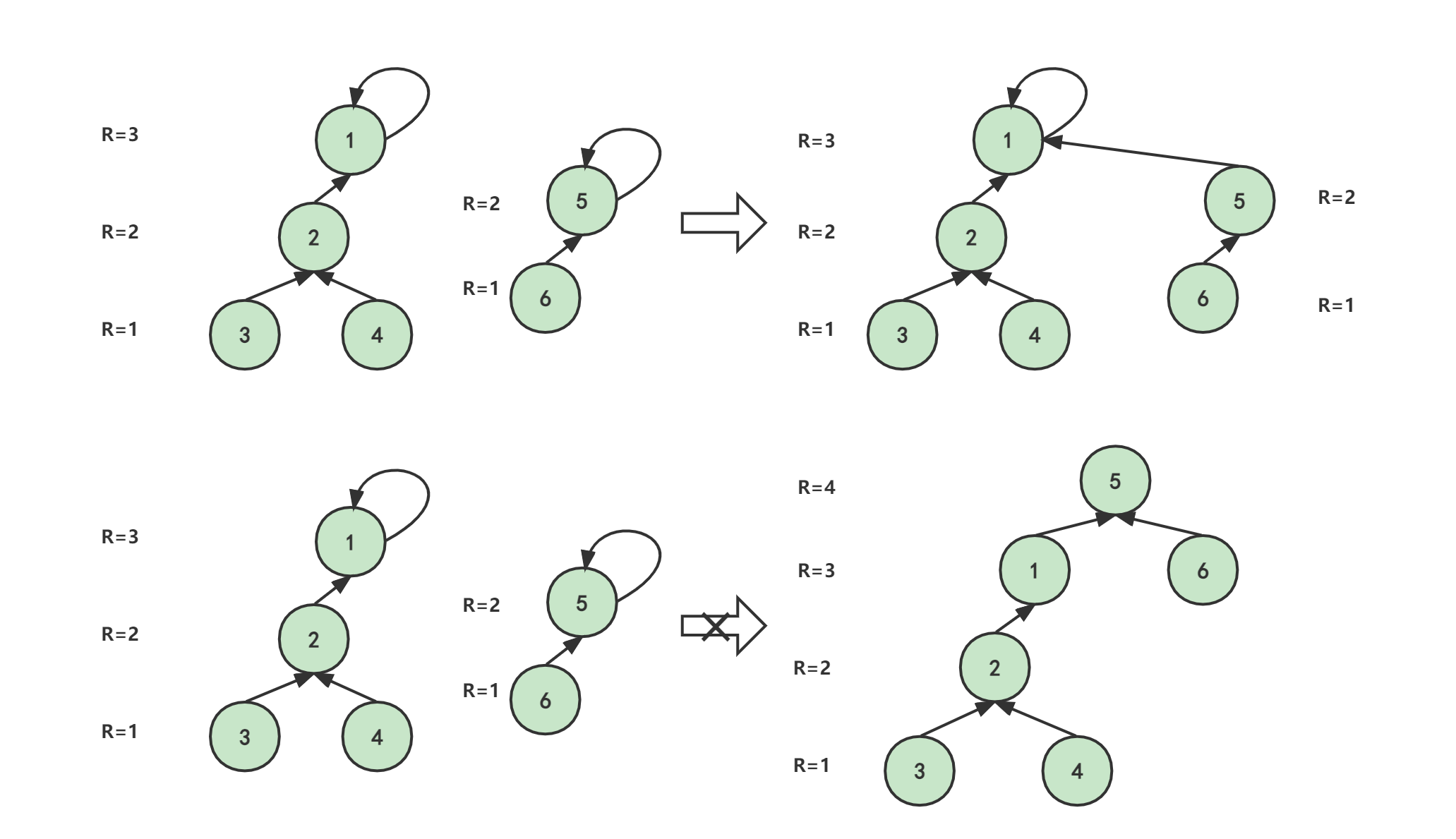
-避免最坏情况：上面说到，查找的最坏情况时间复杂度是O(N)，如何避免最坏情况？

方法：降低查找深度，将深度低的树合并到深度高的树。如下图所示：第一种合并结果高度为4，第二种合并结果高度为3。

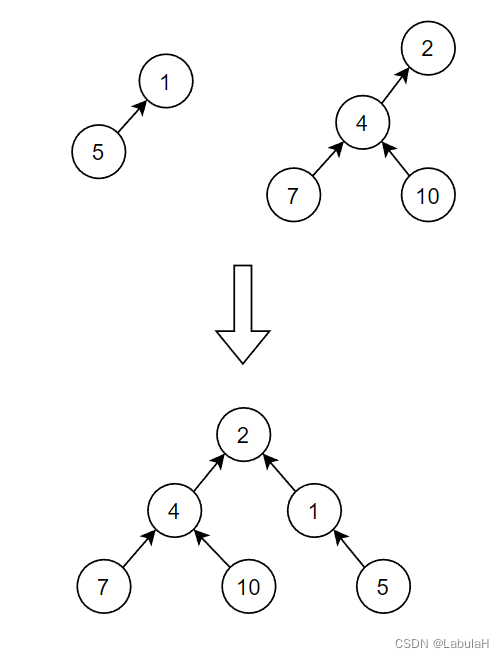
实现：时间复杂度O(1)

merge_3(a, b){if(height(a)==height(b)){height(a) = height(a)+1;Set[b] = a;}else if(height(a)<height(b))Set[a] = b;elseSet[b] = a;
}

效果：最坏情况的时间复杂度变为O(logN)

🎃题目1

Problem - 1232https://acm.hdu.edu.cn/showproblem.php?pid=1232AC代码：

#include<bits/stdc++.h>
using namespace std;int city[1001];
int findBoss(int a){int boss = a;while(city[boss]!=boss){boss = city[boss];}return boss;
}
void changeBoss(int a, int b){int aBoss = findBoss(a);int bBoss = findBoss(b);if(aBoss != bBoss){city[aBoss] = bBoss;}
}int main (){int N, M, x, y, number;while(cin >> N, N){number = -1;for(int i=1; i<=N; i++)city[i] = i;cin >> M;for(int i=0; i<M; i++){cin >> x >> y;changeBoss(x, y);}for(int i=1; i<=N; i++)if(city[i]==i) number++;cout << number << endl;}return 0;
}