文章目录

并查集
- 一、简介
- - 1.定义
  - 2. 并查集的实现与优化
- 二、练习
- - 1.合并集合
  - 2.连通块中点的数量
  - 3. 食物链
- 三、总结

并查集

一、简介

1.定义

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题（即所谓的并、查）。比如说，我们可以用并查集来判断一个森林中有几棵树、某个节点是否属于某棵树等。

2. 并查集的实现与优化

并查集最常见两大操作：

1.将两个集合合并

2.查询某个元素的祖宗节点

基本原理：每个集合用一棵树来表示。树根的编号就是整个集合的编号。每个节点存储它的父节点，p[x]表示x的父节点。

问题1：如何判断树根：if(p[x] == x) （x的父节点指向自己）

问题2：如何求x的集合编号（求x的祖宗节点）（集合编号是这个集合的代表）：while(p[x] != x ) x = p[x]

问题3：如何合并两个集合：将x的根节点嫁接到y的根节点，如：px是x的集合编号，py是y的集合编号，嫁接：p[px] = y

初始化：

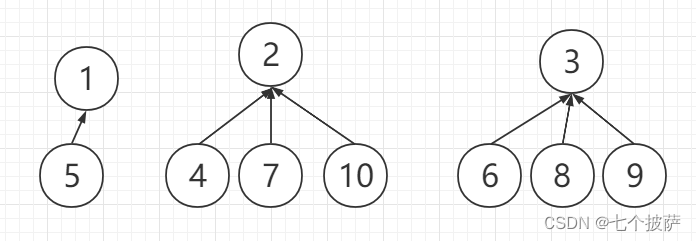
初始时，将每一个节点的父节点指向自己：

for(int i = 0; i < 8; i ++) p[i] = i;

上面的代码实现的结果如下图所示：

在这里插入图片描述

查找x的祖宗节点：

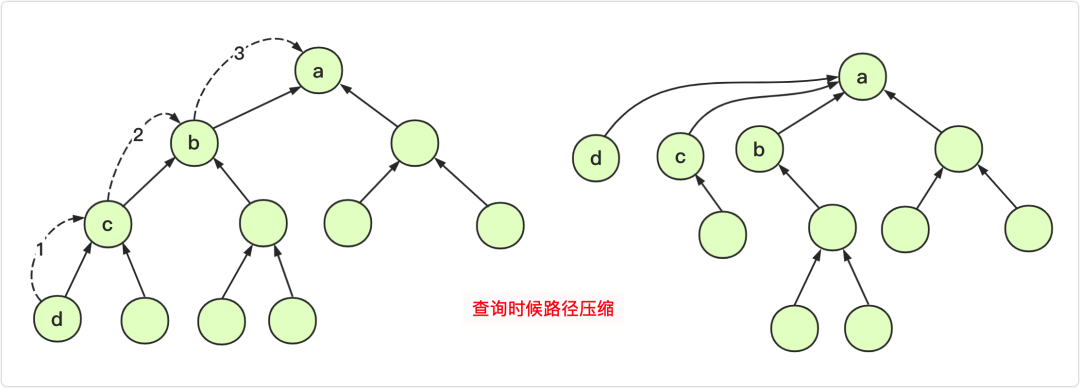
如何求x的集合编号（求x的祖宗节点）：while(p[x] != x ) x = p[x]：每每寻找新的x的祖宗节点都要重新从当前位置遍历逐一寻找父节点直至得到祖宗节点，时间复杂度O(n)，当数据量很庞大时，效率就会比较低。这条搜索路径可能很长。如果在返回的时候，顺便把i所属的集改成根结点，那么下次再搜的时候，就能在O(1)的时间内得到结果。可以通过查找 + 路径压缩的方式优化到近乎O(1)的时间复杂度。

并查集优化：查找 + 路径压缩

上述操作之所以效率不高，那是因为我们使用了太多没用的信息，我的祖先是谁与我父亲是谁没什么关系，这样一层一层找太浪费时间，不如我直接当祖先的儿子，问一次就可以出结果了。甚至祖先是谁都无所谓，只要这个人可以代表我们家族就能得到想要的效果。把在路径上的每个节点都直接连接到根上，这就是路径压缩。

在这里插入图片描述

int find(int x) // 返回x的祖先节点 + 路径压缩
{// x不是根节点，让它的父节点等于(指向)祖宗节点// x 不是自身的父亲，即 x 不是该集合的代表if(p[x] != x) p[x] = find(p[x]); // 查找 x 的祖先直到找到代表，于是顺手路径压缩// 返回x的祖先节点return p[x];
}

find函数的功能是查找祖宗节点，路径压缩的过程其实是一个递归调用与回溯的过程！在递归过程中，从元素i到根结点的所有元素，它们所属的集都被改为根结点。路径压缩不仅优化了下次查询，而且也优化了合并，因为合并时也用到了查询。

在这里插入图片描述

注意图，当我们在查找1的父节点的过程中,路径压缩的实现

针对 x = 1

find(1) p[1] = 2 p[1] = find(2)
find(2) p[2] = 3 p[2] = find(3)
find(3) p[3] = 4 p[3] = find(4)
find(4) p[4] = 4 将p[4]返回

退到上一层
find(3) p[3] = 4 p[3] = 4 将p[3]返回
退到上一层
find(2) p[2] = 3 p[2] = 4 将p[2]返回
退到上一层
find(1) p[1] = 2 p[1] = 4 将p[1]返回

至此，我们发现所有的1，2，3的父节点全部置为了4，实现路径压缩；同时也实现了1的父节点的返回

合并集合：

如何合并两个集合：将a的祖先节点的父节点置为b的祖先节点，就实现了a的根节点嫁接到b的根节点。

p[find(a)] = find(b)

在这里插入图片描述

判断两个元素是否在同一个集合中：

如果两个元素在同一个集合中，说明这个两个元素具有相同的根节点

if(find(a) == find(b)) ----Yes

二、练习

1.合并集合

一共有 nn 个数，编号是 1∼n1∼n，最开始每个数各自在一个集合中。

现在要进行 mm 个操作，操作共有两种：

M a b，将编号为 aa 和 bb 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
Q a b，询问编号为 aa 和 bb 的两个数是否在同一个集合中；

输入格式

第一行输入整数 nn 和 mm。

接下来 mm 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式

对于每个询问指令 Q a b，都要输出一个结果，如果 aa 和 bb 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

1≤n,m≤105

输入样例：

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

输出样例：

Yes
No
Yes

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 0;
int p[N];int find(int x) // 查找 + 路径压缩
{if(x != p[x]) p[x] = find(p[x]);return p[x];
}int main()
{int n ,m;cin >> n >> m;// 初始化集合for(int i = 1; i <= n; i++) p[i] = i;while (m -- ){int a, b;string opt;cin >> opt >> a >> b;if(opt == "M") p[find(a)] = find(b); // 合并两个集合：a的根节点的父节点指向b的根节点else {// 判断两个元素是否位于同一个集合if(find(a) == find(b)) cout << "Yes" << endl;else cout << "No" << endl;}}return 0;
}

2.连通块中点的数量

并查集维护集合（连通块）中点的个数！

给定一个包含 nn 个点（编号为 1∼n1∼n）的无向图，初始时图中没有边。

现在要进行 mm 个操作，操作共有三种：

C a b，在点 aa 和点 bb 之间连一条边，aa 和 bb 可能相等；
Q1 a b，询问点 aa 和点 bb 是否在同一个连通块中，aa 和 bb 可能相等；
Q2 a，询问点 aa 所在连通块中点的数量；

输入格式

第一行输入整数 nn 和 mm。

接下来 mm 行，每行包含一个操作指令，指令为 C a b，Q1 a b 或 Q2 a 中的一种。

输出格式

对于每个询问指令 Q1 a b，如果 aa 和 bb 在同一个连通块中，则输出 Yes，否则输出 No。

对于每个询问指令 Q2 a，输出一个整数表示点 aa 所在连通块中点的数量

每个结果占一行。

数据范围

1≤n,m≤1051≤n,m≤105

输入样例：

5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5

输出样例：

Yes
2
3

思路：

用集合来维护连通块

操作1：两个连通块之间连一条边 ——> 将两个集合合并

操作2：询问点 a 和点 b 是否在同一个连通块中 ——> 判断两个元素是否在同一个集合中

操作3：询问点 a 所在连通块中点的数量 ——> 统计集合中每个点的数量

操作1，2同朴素的合并集合操作，对于操作3，我们可以用一个sizes[]数组来记录集合的大小（集合中点的个数），通过sizes数组得出集合的大小。

那我们如何维护sizes数组呢？

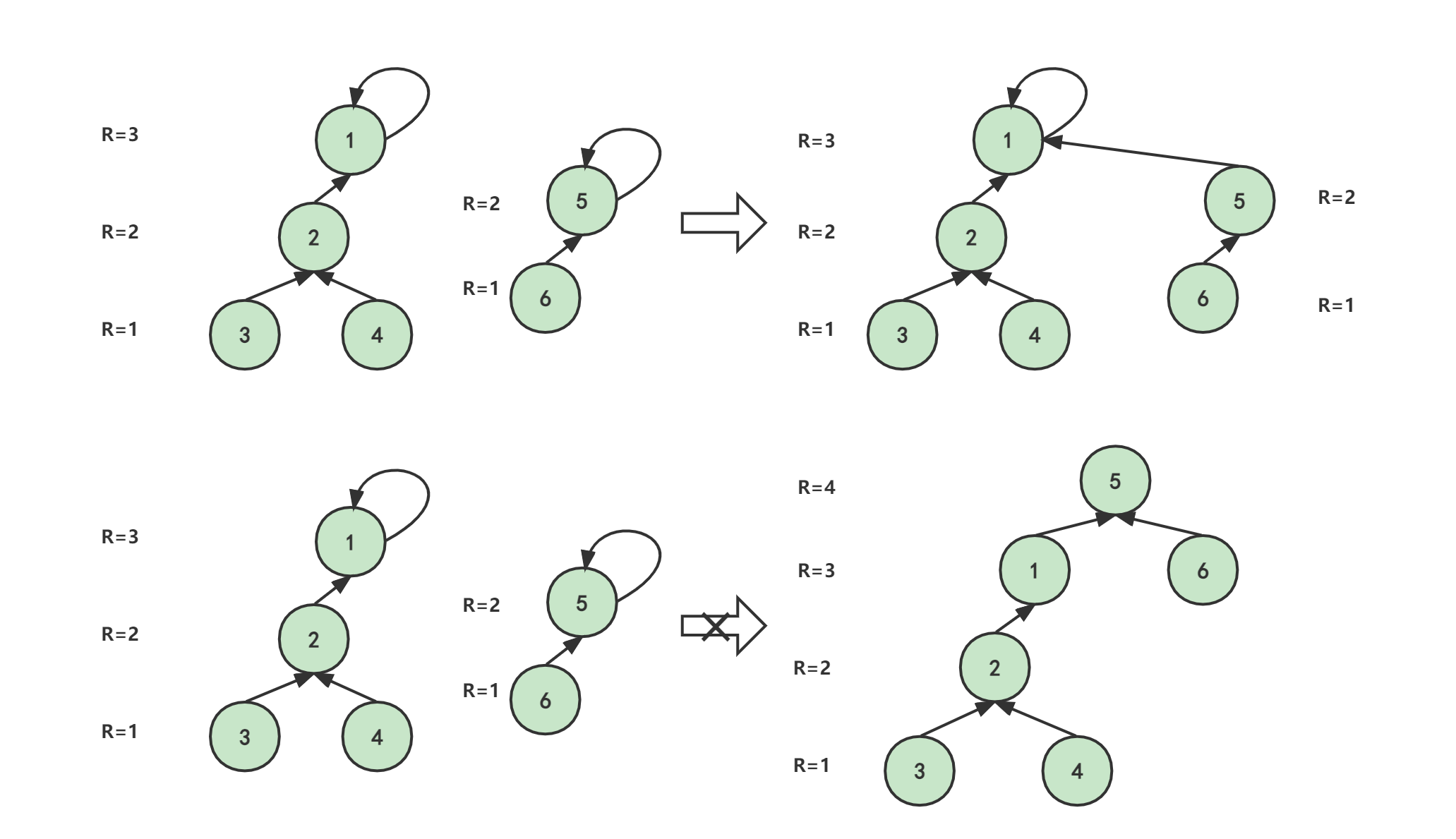
我们规定只有根节点的sizes是有意义的：每一个集合对应一棵树，因此我们只需要保证根节点的sizes有意义即可，其实我们只要在合并两个集合的时候，把集合的大小加到其祖宗集合上面去就行了。

我们如何更新sizes数组呢？

当我们需要进行合并操作时（将集合x的根节点为a，集合y的根节点为b ，将集合x合并到集合y），我们只需要更新集合b的sizes即可，即：sizes[b] += size[a]，合并后的集合的根节点b的sizes就为两个集合的大小。

**最后我们如何得出元某一素(a)所在集合的集合个数（大小呢）？**在上面的讲述中我们知道，之和的大小由根节点的sizes来维护，因此size[find(a)]即为该集合的大小。

注：下图中的a，b为别为两个集合的根节点！

在这里插入图片描述

值得注意的是：当两个集合已经是同一个集合了，就不需要在进行合并操作，即不用更新sizes数组，因此在合并操作时需要特判一下，看两个元素是否属于同一个集合！

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10;
//p[N]存储每个节点的父节点，size[N]记录集合的大小
int p[N], sizes[N];int find(int x) // 查找x的根节点 + 路径压缩
{if(p[x] != x) p[x] = find(p[x]);return p[x];
}int main()
{int n, m;cin >> n >> m;for(int i = 1; i <= n; i++) // 初始化集合{p[i] = i;sizes[i] = 1; // 刚刚开始每个集合中只有一个元素，因此初始化为1}while(m --){int a, b;string opt;cin >> opt;if(opt == "C"){cin >> a >> b;if(find(a) == find(b)) continue; //特判： 如果两个集合已经在同一个集合中了，就不需要合并了// 先更新size在合并，如果先合并在更新size，两个集合的根节点此时已经变为同一个根节点了，那么根节点对应的size就发生了变化sizes[find(b)] += sizes[find(a)]; //两集合合并sizes更新：将a所有连线的数+b所有连线的点数 p[find(a)] = find(b); // 将集合a的根节点的父节点指向b集合的根节点}else if(opt == "Q1"){cin >> a >> b;if(find(a) == find(b)) cout << "Yes" << endl;else cout << "No" << endl;}else{cin >> a;cout << sizes[find(a)] << endl;}}return 0;
}

3. 食物链

【题目链接】240. 食物链 - AcWing题库

动物王国中有三类动物 A,B,C，这三类动物的食物链构成了有趣的环形。

A 吃 B，B 吃 C，C 吃 A。

现有 NN 个动物，以 1∼N 编号。

每个动物都是 A,B,C 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 N 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 X 和 Y 是同类。

第二种说法是 2 X Y，表示 X 吃 Y。

此人对 N 个动物，用上述两种说法，一句接一句地说出 K 句话，这 K 句话有的是真的，有的是假的。

当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话；
当前的话中 X 或 Y 比 N 大，就是假话；
当前的话表示 X 吃 X，就是假话。

你的任务是根据给定的 N 和 K 句话，输出假话的总数。

输入格式

第一行是两个整数 N 和 K，以一个空格分隔。

以下 K 行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中 D 表示说法的种类。

若 D=1，则表示 X 和 Y 是同类。

若 D=2，则表示 X 吃 Y。

输出格式

只有一个整数，表示假话的数目。

数据范围

1≤N≤50000,
0≤K≤100000

输入样例：
100 7
1 101 1 
2 1 2
2 2 3 
2 3 3 
1 1 3 
2 3 1 
1 5 5
输出样例：
3

并查集之边带权
思路：只要有关系，就属于同一个集合，就加入到集合中去（不管是同类or异类）
所以边带权的并查集问题本质上只在维护多个集合。

精髓：只要两个元素在同一个集合里，就能通过他们与根节点的距离知道他们之间的关系。

距离的定义?
用“距离”来描述关系、判断关系，所有的距离都以根节点为基准，按照mod类别数(3)分为3类（每3个一个循环）。
“距离”：x吃y表示y到x的距离为1. y是第0代，吃y的x是第1代，吃x的是第2代…根节点是第0代
三种关系：用点到根节点之间的距离表示其余根节点之间的关系
mod 3 = 1:可以吃根节点
mod 3 = 2:可以被根节点吃
mod 3 = 0:和根节点同类
把集合中所有的点划分为上述三类。

在这里插入图片描述

两个数组的定义：
p[]:父节点,
d[]:到父节点（不是根节点）的距离(初始是1，随着路径压缩会逐渐增大)
我们只能获得点到其直接父节点的距离。路径压缩和更新边权的时候也是这样。

find()函数解释：

int find(int x)
{if(x != p[x]){int u = find(p[x]);d[x] += d[p[x]];p[x] = u;}return p[x];
}

u = find(p[x])先把父节点及以上压缩到根节点，这时父节点是根节点的一级子节点，x是根节点的二级子节点。过程中d[p[x]]被更新为父节点到根节点的距离。

d[x] += d[p[x]]; p[x] = u;先更新边权，再把x也压到根节点。否则x的父节点到根节点的距离d[p[x]]没加上就丢失了

在这里插入图片描述

容易弄混d[x]到底是到父节点还是根节点的距离：

事实上，d[x]始终代表到父节点的距离，只不过在find之后x的父节点直接变成了祖宗，所以逻辑上成了到祖宗的距离。

（只不过是经过路径压缩和加和操作之后，d[x]就是x到根节点的距离，而此时的根节点同时也x的父节点！）

最后，什么样的话才是假话呢？

当前的话中 X 或 Y 比 N 大，就是假话
另外两种情况，当发生矛盾时就是假话
- 若 D=1，则表示 X 和 Y 是同类。-----> 若判断出输入的x与y不满足是同类的条件，则说明它是假话
- 若 D=2，则表示 X 吃 Y。-----> 若判断出输入的x与y不满足是x吃y的条件，则说明它是假话

具体判断解释如下：

若x与y在同一个集合中，就可以知道两者的关系。
- （1）x与y是同类---->d[x]%3 = d[y]%3 ，即(d[x] - d[y])%3==0。如果不满足此条件，说明输入的x和y不是同一类型，即为假话
- （2）x吃y---->x到根的距离比y到根的距离多1：(d[x] - d[y] -1) % 3 == 0，如果不满足此条件，则为假话
若x与y不在同一个集合中，说明x和 y 还没有关系，可以进行合并

在这里插入图片描述

【代码实现】

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 50000 + 10;
int p[N];
int d[N];//d[x]表示x到它父节点的距离。全局变量，初始都为0了 int n, m;int find(int x)  // 并查集
{if (p[x] != x){int u = find(p[x]);d[x] += d[p[x]];p[x] = u;}return p[x];
}int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++) p[i] = i;// 初始化并查集int res = 0;//假话个数while (m -- ){int t, x, y;//t表示x与y的关系种类cin >> t >> x >> y;if(x > n || y > n) res ++;//当前的话中 X 或 Y 比 N 大，就是假话；else{int px = find(x), py = find(y);// 拿到各自的集合编号if(t == 1)// 情况1：x 与 y 为类，我们要判断是不是{if(px == py && (d[x] - d[y]) % 3 != 0) res ++;// 连通：若不满足是同类的条件，即为假话else if(px != py)//不连通：将它们合并{p[px] = py;// 合并d[px] = d[y] - d[x];}}else// 情况2：x 吃 y{if(px == py && (d[x] - d[y] -1) % 3 != 0) res ++;else if(px != py){p[px] = py;d[px] = d[y] + 1 - d[x];}}}}cout << res;return 0;
}