一、概述

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。

其实说白了大部分还是用于寻找两个点是否联通，求最小生成树。

二、分析

1、背景阐明

首先我们需要先阐明一个简单的道理，假如从A城能到B城，从B城能到C城，那么自然A城和C城联通。并查集便是基于这个理论。

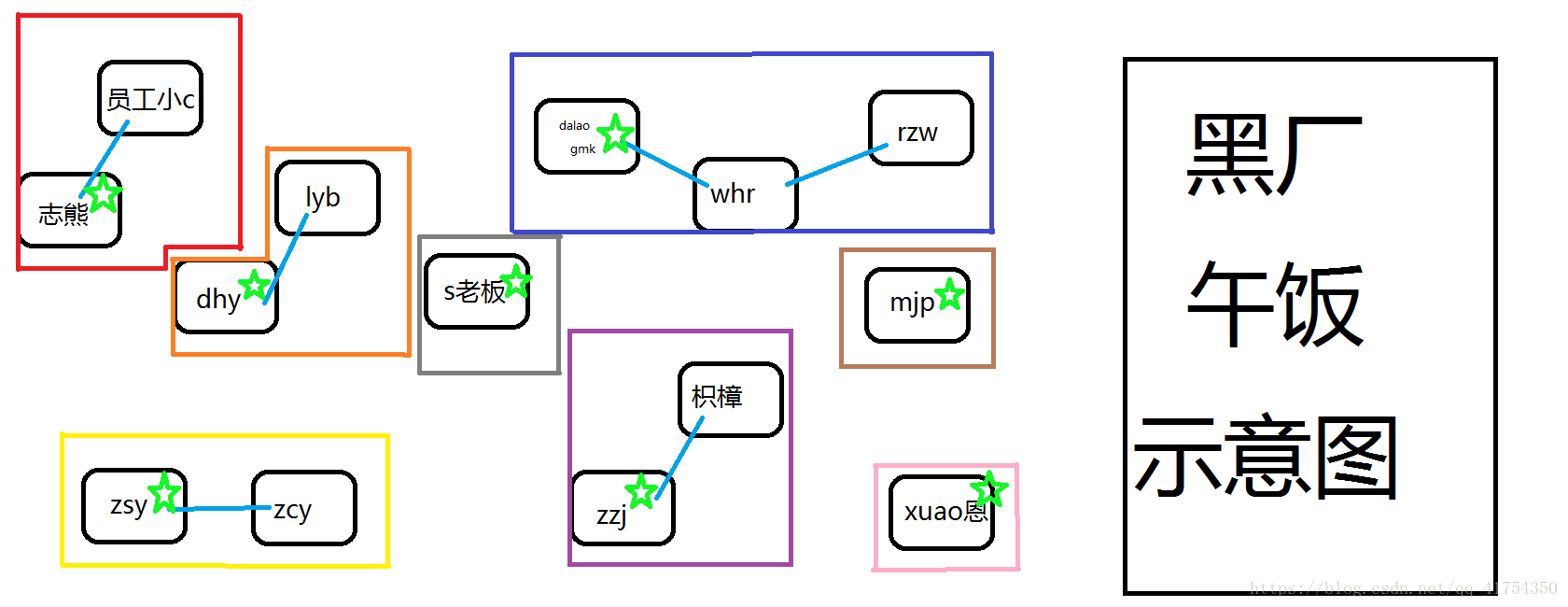
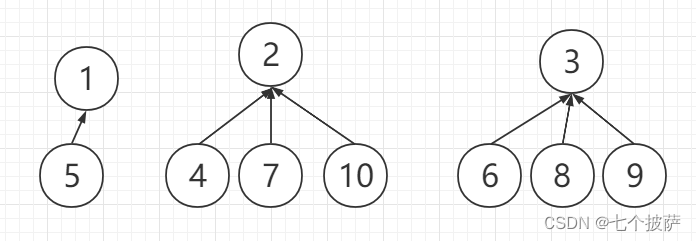
举个例子，在某黑厂中，员工们吃饭时往往三两成群（每个小群体都有一个比较有主见的人决定中午吃什么，当然，两个很主见的人不可能在一个小集体，但是有的可能仅仅是为了和朋友在一起，并不关心到底吃什么），比如志熊喜欢拉上员工小C一起出去吃，gmk喜欢和whr、rzw三人在食堂解决，而xuao恩自己带饭。于是大概就变成了这样一张图：

（头上原谅星的是这个团队里的主心骨）

2、查找

假如说员工小C的外校朋友小D想和小C一起吃个饭追溯一下革命友情（手动滑稽），他会找小C这个集团的主心骨协商会面，很可惜，小C不是这个集团的主心骨，那如何找到呢？

闲话不多说，直接上代码来理解。

我们定义一个find函数和一个数组f[ ]（用来记录他“想跟随”的朋友）。

int find(int x){return f[x]==x?x:(f[x]=find(f[x]));}

3、合并

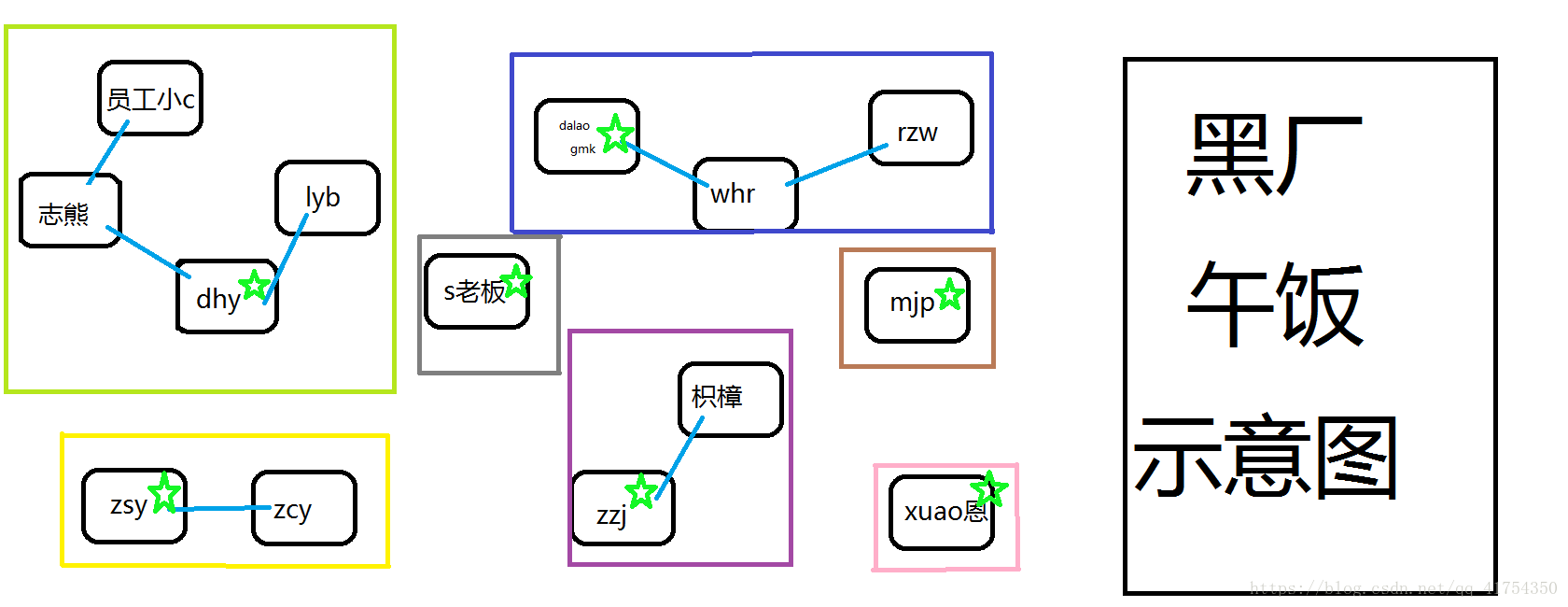
有一天，员工小C跟随的好友志熊觉得跟学长lyb和dhy混也不错，于是他们决定加入他们。

于是图变成了这样：

志熊决定跟随学长dhy，所以吃什么已经不由他来决定了（头上的原谅星也随之消失），如图志熊选择跟随dhy，小C认为还是和朋友在一起好，也会跟随志熊，lyb如常跟随dhy，这样新的四人团体就构成了。

然而代码如何实现呢，这非常简单：

void join(int x,int y)
{father[find(x)]=find(y);
}

4、路径压缩

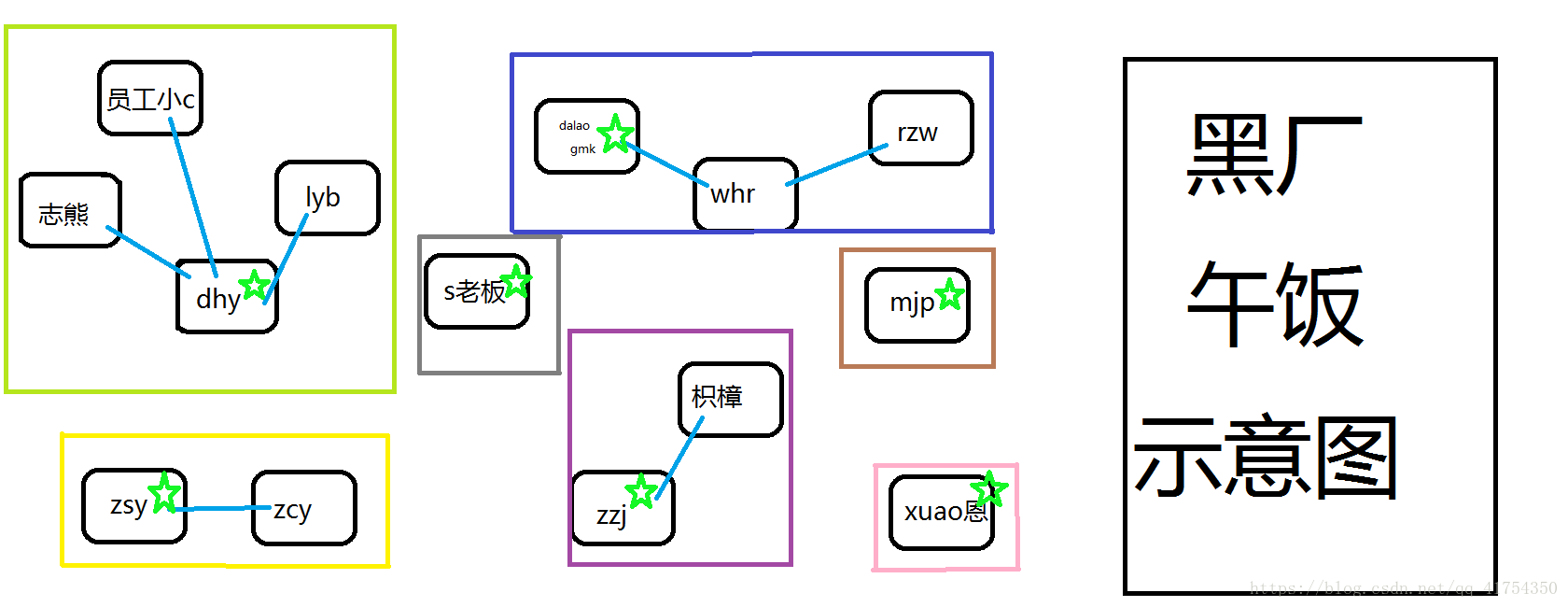
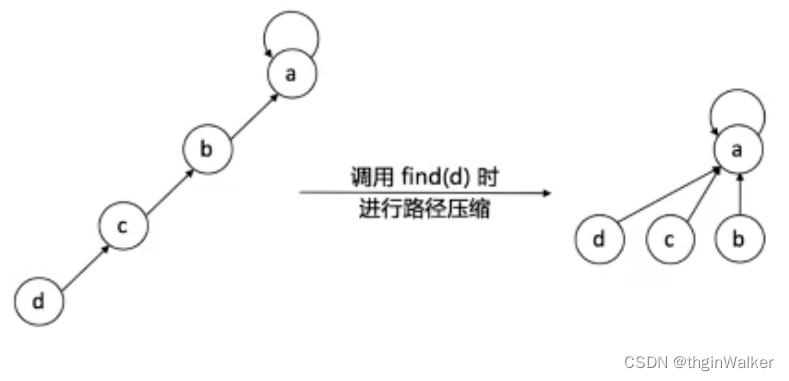
员工小C有一天突然觉得和学长密切交流的机会不能全给志熊啊，他决定直接跟随学长dhy，不再跟随志熊了。

如下图所示：

而这一步代码如何实现呢：

int zip(int x)//路径压缩
{if(pre[x]!=x)//如果它的前驱节点不是他自己//（他不是这个小团体的主心骨） pre[x]=find(pre[x]);//他直接跟随老大 return x;
}

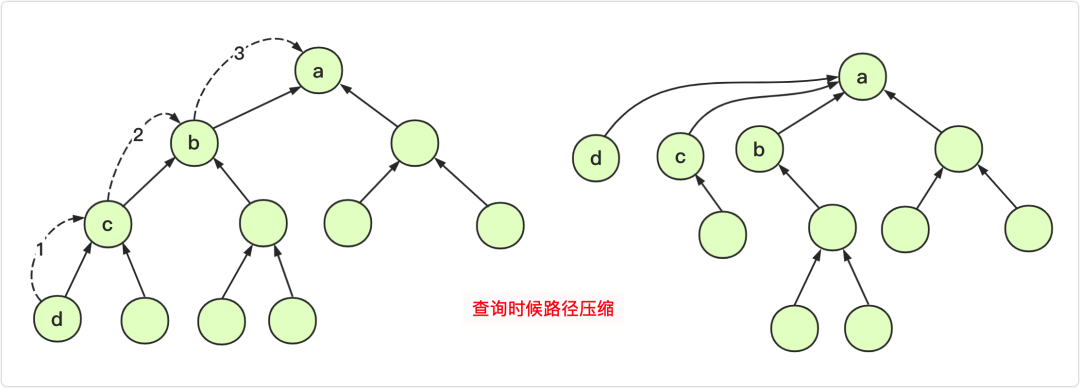
我们可以看到经过路径压缩的节点及其子树到根节点的深度减小了很多，所以在以后的操作中，查找根节点的速度会快很多，这就是路径压缩的意义。

5、按秩排序

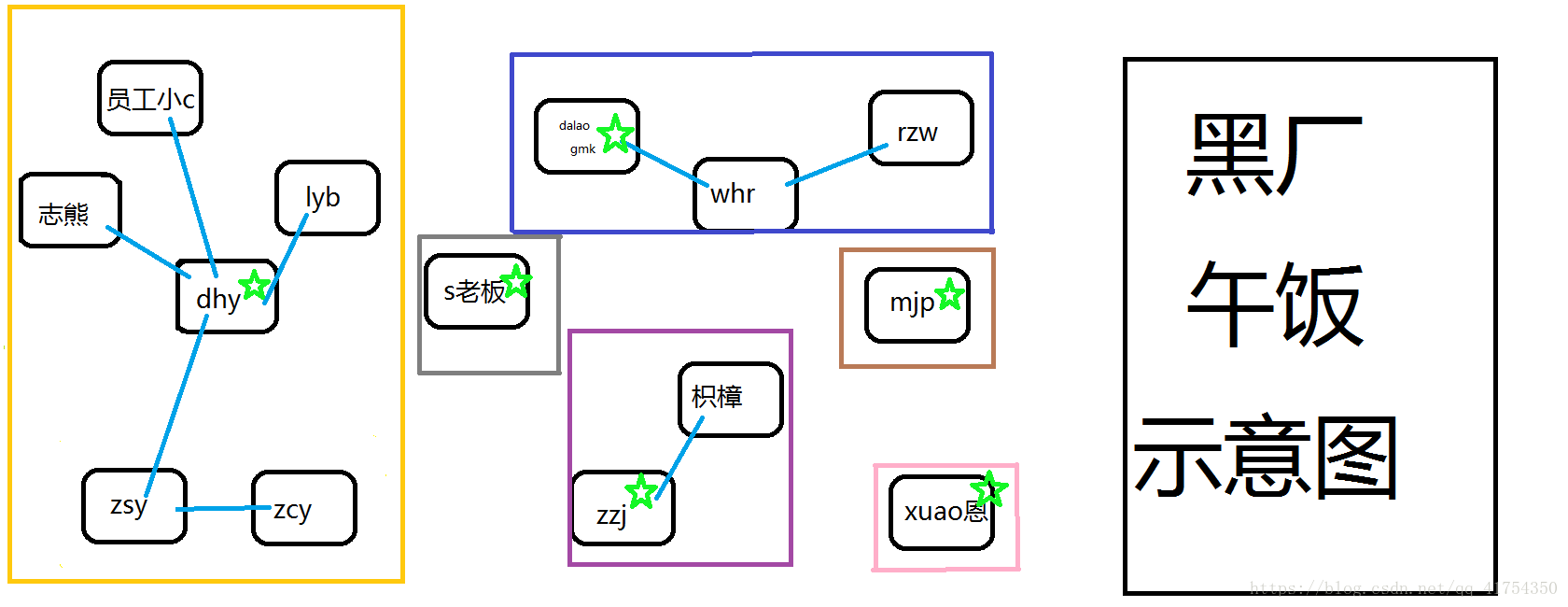
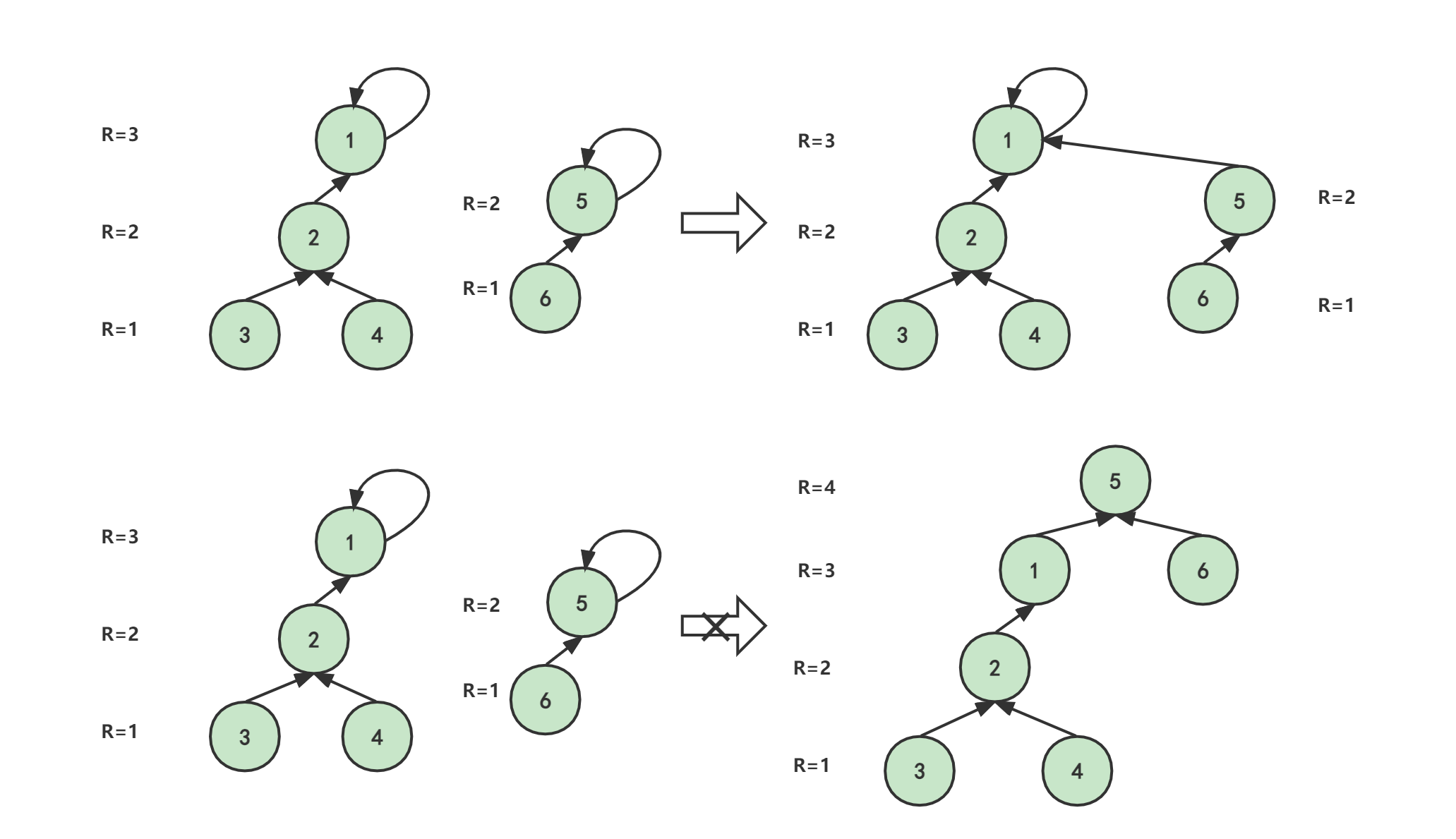
zsy看到了两个集团的合并，决定也加入他们，此时zsy有一个伙伴，而dhy有三个。人多力量大么，自然人少了要向人多的靠拢，如图所示：

上代码：

void unionn(int r1,int r2)//秩排序 rank用来记录随从的多少 
{int fr1=find(r1);//找到r1团队的主心骨 int fr2=find(r2);//找到r2团队的主心骨 if(fr1==fr2)//自己人，走吧 return;if(rank[fr1]>=rank[fr2])//r1的人多 {f[fr2]=fr1;//r2成为r1的一部分 rank[fr1]+=rank[fr2];//r1多了很多"随从" }else//r2的人多{f[fr1]=fr2;//r1成为r2的一部分 rank[fr2]+=rank[fr1];//r2多了很多"随从" }
}

当然每次别忘了把rank数组初始化（在输入的同时）

对于并查集来说，这是一种优化，将小树移到大树上，可以有效降低整个树的深度。

6、并查反集

我也是才发现了这个问题

[BOI2003]团伙

题目描述
给定 nn 个人，他们之间有两个种关系，朋友与敌对。可以肯定的是：与我的朋友是朋友的人是我的朋友
与我敌对的人有敌对关系的人是我的朋友
现在这 nn 个人进行组团，两个人在一个团队内当且仅当他们是朋友。求最多的团体数。输入格式
第一行一个整数 nn 代表人数。
第二行一个整数 mm 代表每个人之间的关系。
接下来 mm 行每行一个字符 optopt 与两个整数 p,qp,q如果 optopt 为 F 代表 pp 与 qq 为朋友。
如果 optopt 为 E 代表 pp 与 qq 为敌人。
输出格式
一行一个整数代表最多的团体数。输入输出样例
输入 #1复制
6
4
E 1 4
F 3 5
F 4 6
E 1 2
输出 #1复制
3
说明/提示
对于 100\%100% 的数据，2 \le n \le 10002≤n≤1000，1 \le m \le 50001≤m≤5000，1 \le p,q \le n1≤p,q≤n。

#include<bits/stdc++.h>
using namespace std;
int s,n,m,a,b,f[2500];
char ch;
int find(int x){if(f[x]!=x)f[x]=find(f[x]);//查找+路径压缩，如果没有祖先就回溯return f[x];
}
int main(){cin>>n>>m;for(int i=1;i<=2*n;i++){f[i]=i;//初始化，千万不能漏}for(int i=1;i<=m;i++){cin>>ch>>a>>b;if(ch=='F'){f[find(a)]=find(b);//合并}else{f[find(a+n)]=find(b);//printf("<%d的父亲是%d>\n",find(a+n),find(b)) ;f[find(b+n)]=find(a);//printf("<%d的父亲是%d>\n",find(b+n),find(a)) ;//反集合并}}for(int i=1;i<=n;i++){if(f[i]==i)s+=1;}cout<<s;//祖先数就是团伙数
}

当a与b结仇，相当于黑化a的大哥是b。之后a又与c结仇，此时黑化a的大哥是b，并查集一下，b的大哥就成了c。