并查集Python版

article/2025/8/27 0:02:45

以下来自于leetcode

使用数据结构：并查集

思路：由于相等关系具有传递性，所有相等的变量属于同一个集合；
只关心连通性，不关心距离，因此很容易想到并查集。（很容易嘛，反正我想不到）

并查集

「并查集」用于判断一对元素是否相连，它们的关系式动态添加的，这一类问题叫做「动态连通性」问题；
主要支持「合并」与「查询是否在同一个集合」操作；
底层结构是「数组」或者「哈希表」，用于表示「节点」指向「父节点」，初始化时指向自己；
「合并」就是把一个集合的根节点指向另一个集合的根节点，只要根节点一样，就表示在同一个集合里；
这种表示「不相交集合」的方法称之为「代表元法」，以每个结点的根节点作为一个集合的「代表元」。
「路径压缩」和「按秩压缩」一起使用的时候，难以维护「秩」准确的定义，但依然具有参考价值。
同时使用「路径压缩」和「按秩合并」，「合并」与「查询」的时间复杂度接近O(1)；
「并查集」的时间复杂度分析，可以在互联网上搜索相关资料学习；
一般而言，「路径压缩」和「按秩合并」使用其中一个即可。

并查集的应用

最小生成树：Kruskal算法

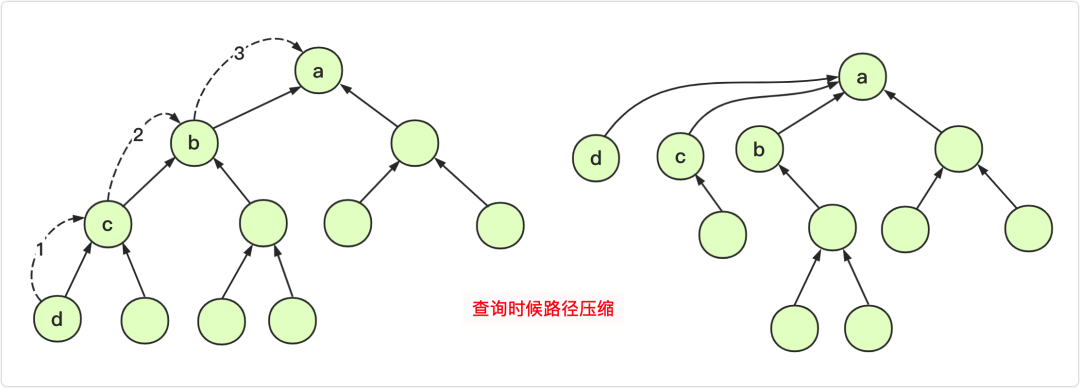
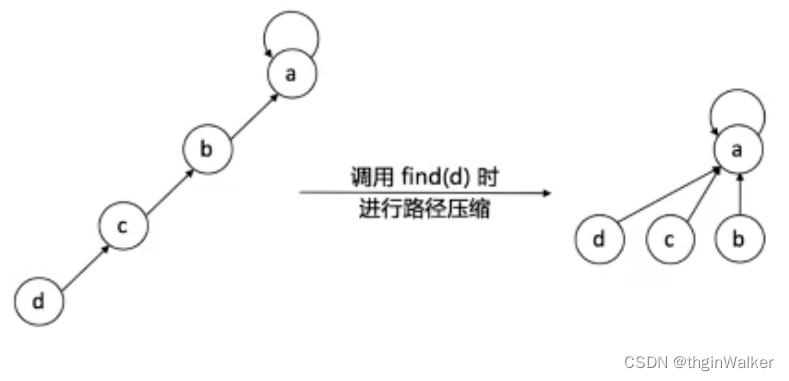
并查集的优化1：路径压缩(Path Compression)

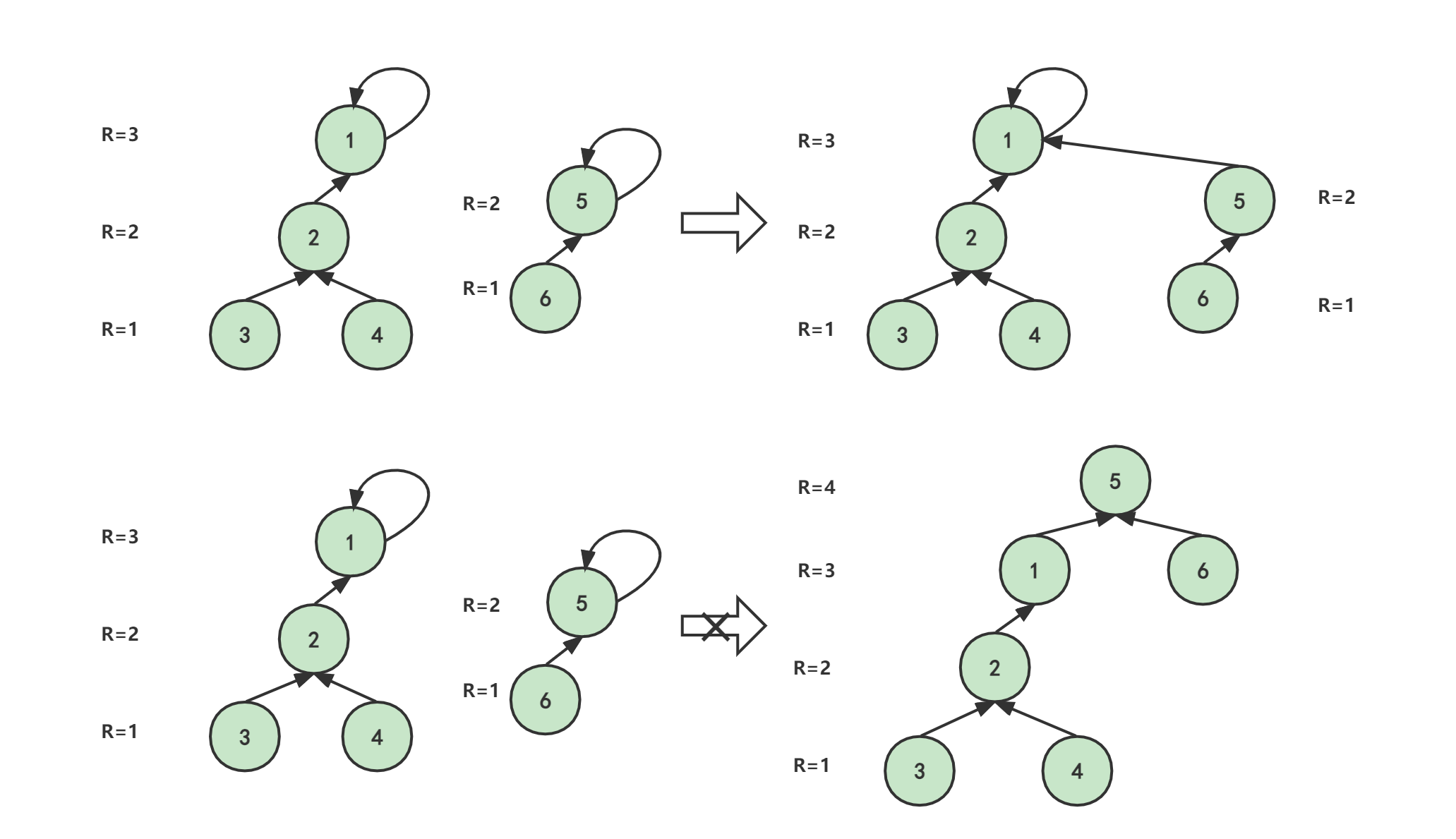
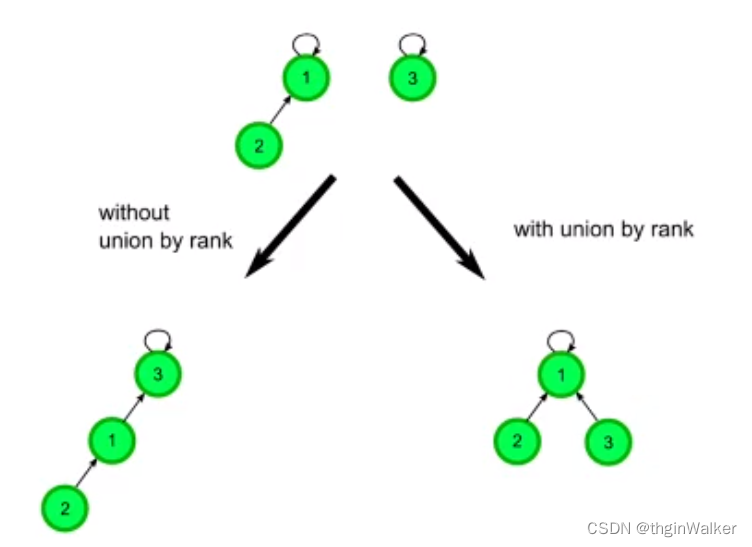
并查集的优化2：按「秩」(Rank)合并

「按秩合并」是指在合并的过程中，使得「高度」更低的树的根节点指向「高度」更高的根节点，以避免合并以后的树高度增加；
990.等式方程的可满足性。

以下来自于算法视频笔记
并查集(union & find)是一种树型的数据结构，用于处理一些不交集(Disjoint Sets)的合并及查询问题。
Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
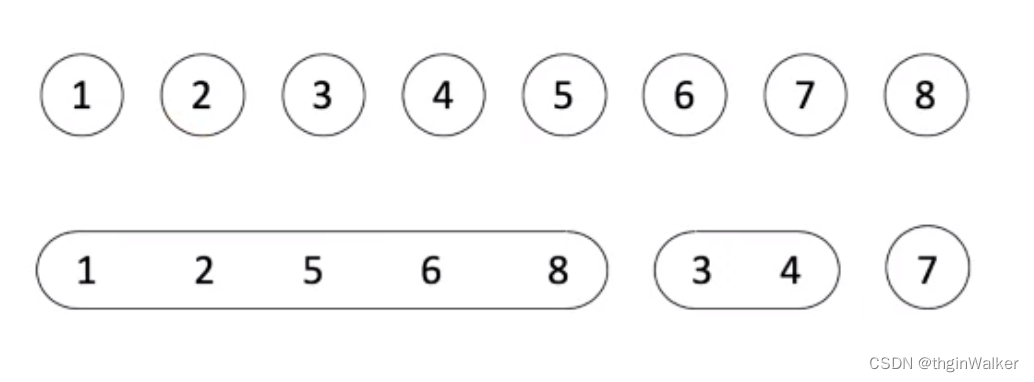
Union：将两个子集合并成同一个集合。

在生活中的例子

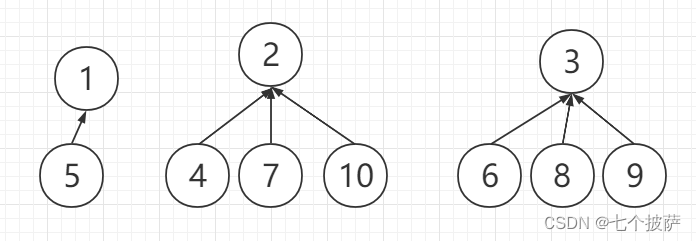
小弟——>老大
帮派识别
两种优化方式

初始化

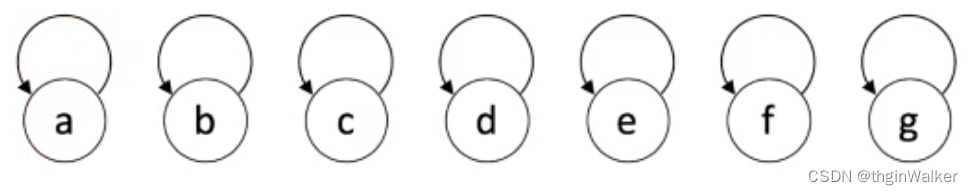
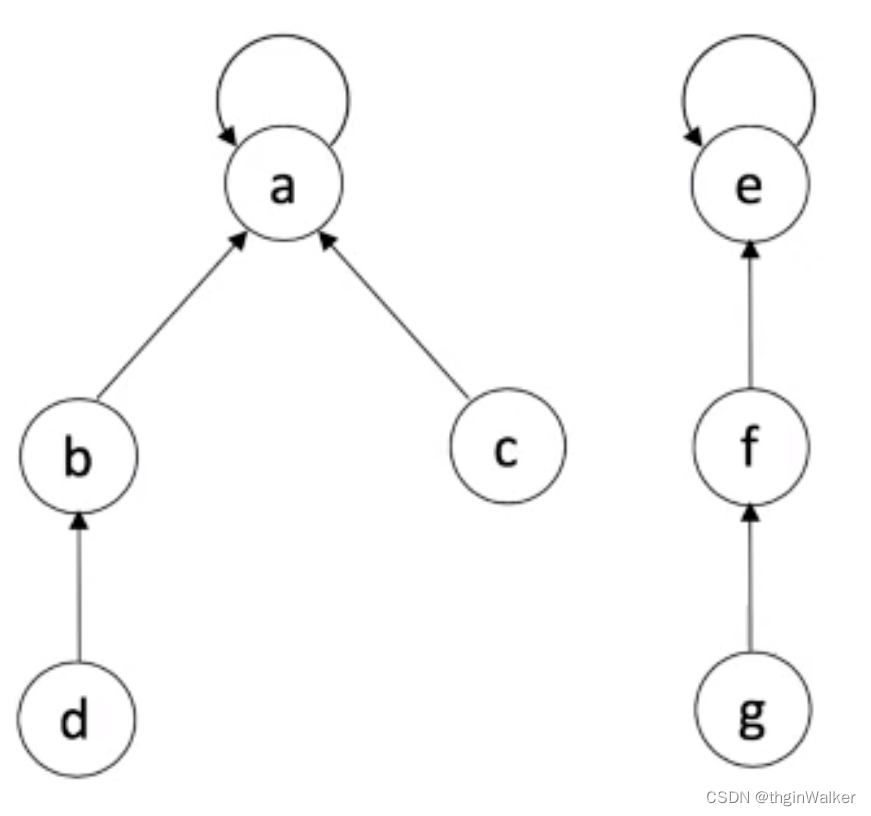
在这里插入图片描述

并查集原始版代码

class baseUnion:# n为节点大小def __init__(self, n):self.parent = list(range(n))  # 从0开始# 查找(递归)def recursion_find(self, index):if self.parent[index] != index:self.parent[index] = self.find(self.parent[index])return self.parent[index]# 查找(迭代,效率更高)def iteration_find(self, index):root = indexwhile root != self.parent[root]:root = self.parent[root]return self.parent[root]  # 或者返回root# 连接def union(self, index1, index2):self.parent[self.iteration_find(index1)] = self.recursion_find(index2)

并查集优化一

在这里插入图片描述

class rank_union:# n为节点大小def __init__(self, n):self.parent = list(range(n))  # 从0开始self.rank = [0] * n# 查找和基本并查集不变# 查找(迭代,递归也可以)def find(self, index):root = indexwhile root != self.parent[root]:root = self.parent[root]return self.parent[root]  # 或者返回root# 连接def union(self, index1, index2):rootx = self.find(index1)rooty = self.find(index2)# 如果不在同一连通分量里进行连接if rootx != rooty:if self.rank[rootx] > self.rank[rooty]:self.parent[rooty] = rootxelif self.rank[rootx] < self.rank[rooty]:self.parent[rootx] = rootyelse:  # 随便选一个self.parent[rooty] = rootxself.rank[rootx] += 1

并查集优化二

优化二效率更高，直接指向根节点，不需要添加rank属性。
在这里插入图片描述

# 效率更高，不需要添加rank属性(实际情况不明显)
class path_compression_union:# n为节点大小def __init__(self, n):self.parent = list(range(n))  # 从0开始self.rank = [0] * n# 查找和基本并查集不变# 查找(迭代,递归也可以)def find(self, index):root = indexwhile root != self.parent[root]:  # 找根节点root = self.parent[root]while index != self.parent[index]:  # 路径压缩tmp = self.parent[index]self.parent[index] = rootindex = tmpreturn self.parent[root]  # 或者返回root# 连接def union(self, index1, index2):self.parent[self.find(index1)] = self.find(index2)

实战题目

number-of-islands
friend-circles

岛屿个数

方法一：染色问题(FloodFill)
A.遍历节点：

if node == '1':count++;将node和附近节点->'0'; # DFS BFS
else:不管;

具体代码:

class Solution(object):self.dx = [-1,1,0,0]self.dy = [0,0,-1,1]def numIslands(self,grid):if not grid or not grid[0]: return 0self.max_x = len(grid); self.max_y = len(grid[0]); self.grid = grid;self.visited = set()return sum([self.floodfill_DFS(i,j) for i in range(self.max_x) for j in range(self.max_y)])def floodfill_DFS(self,x,y):if not self._is_valid(x,y):return 0self.visited.add((x,y))for k in range(4):self.floodfill_DFS(x + dx[k],y + dy[k])return 1def floodfill_BFS(self,x,y):if not self._is_valid(x,y):return 0self.visited.add((x,y))queue = collections.deque()queue.append((x,y))while queue:cur_x,cur_y = queue.popleft()for i in range(4):new_x,new_y = cur_x + dx[i],cur_y + dy[i]if self._is_valid((new_x,new_y))self.visited.add((new_x,new_y))queue.append((new_x,new_y))return 1def _is_valid(self,x,y):if x < 0 or x >= self.max_x or y < 0 or y >= self.max_y:return Falseif self.grid[x][y] == '0' or ((x,y) in self.visited):return Falsereturn True

方法二：并查集
A.初始化：针对’1’结点
B.遍历所有节点，相邻节点合并；'1’合并，'0’不管
C.遍历(找不同的parents,可以在第二步进行统计)

class UnionFind(object):def __init__(self,grid):m,n = len(grid),len(grid[0])self.count = 0self.parent = [-1] *(m+n)self.rank = [0] * (m+n)for i in range(m):for j in range(n):if grid[i][j] == '1':self.parent[i*n + j] = i*n + j # 二维坐标转为一维self.count += 1 # 初始化加一def find(self,i): # 递归if self.parent[i] != i:self.parent[i] = self.find(self.parent[i])return self.parent[i]def union(self,x,y):rootx = self.find(x)rooty = self.find(y)if rootx != rooty:if self.rank[rootx] > self.rank[rooty]:self.parent[rooty] = rootxelif self.rank[rootx] < self.rank[rooty]:self.parent[rootx] = rootyelse:self.parent[rooty] = rootxself.rank[rootx] += 1self.count -= 1 # 合并减一class Solution(object):def numIslands(self,grid):if not grid or not grid[0]:return 0uf = UnionFind(grid)directions = [(0,1),(0,-1),(-1,0),(1,0)]m,n = len(grid),len(grid[0])for i in range(m):for j in range(n):if grid[i][j] == '0':continuefor d in directions:nr,nc = i + d[0],j + d[1]if nr >= 0 and nc >= 0 and nr < m and nc < n and grid[nr][nc] == '1':uf.union(i*n+j,nr*n+nc)return uf.count