---

并查集的原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。

并查集一般可以解决以下问题：

1. 查找元素属于哪个集合
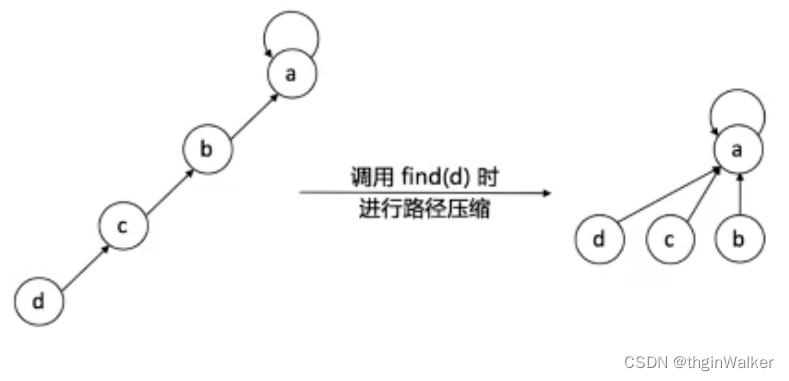
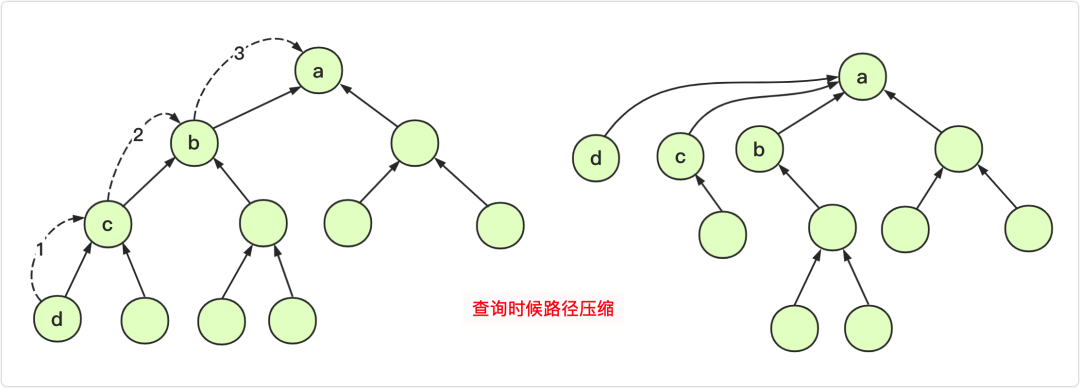
   沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)。
2. 查看两个元素是否属于同一个集合
   沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在。
3. 将两个集合归并成一个集合
   将两个集合中的元素合并，或者将两个元素的根进行合并。
4. 集合的个数
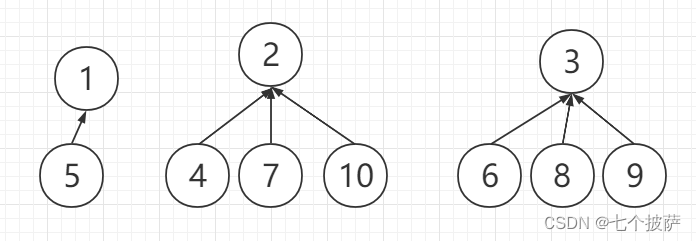
   遍历数组，数组中元素为负数的个数即为集合的个数。

---

并查集的实现代码

使用数组（vector）实现：

#include<iostream>
#include<vector>
#include<assert.h>
using namespace std;
class UnionFindSet
{
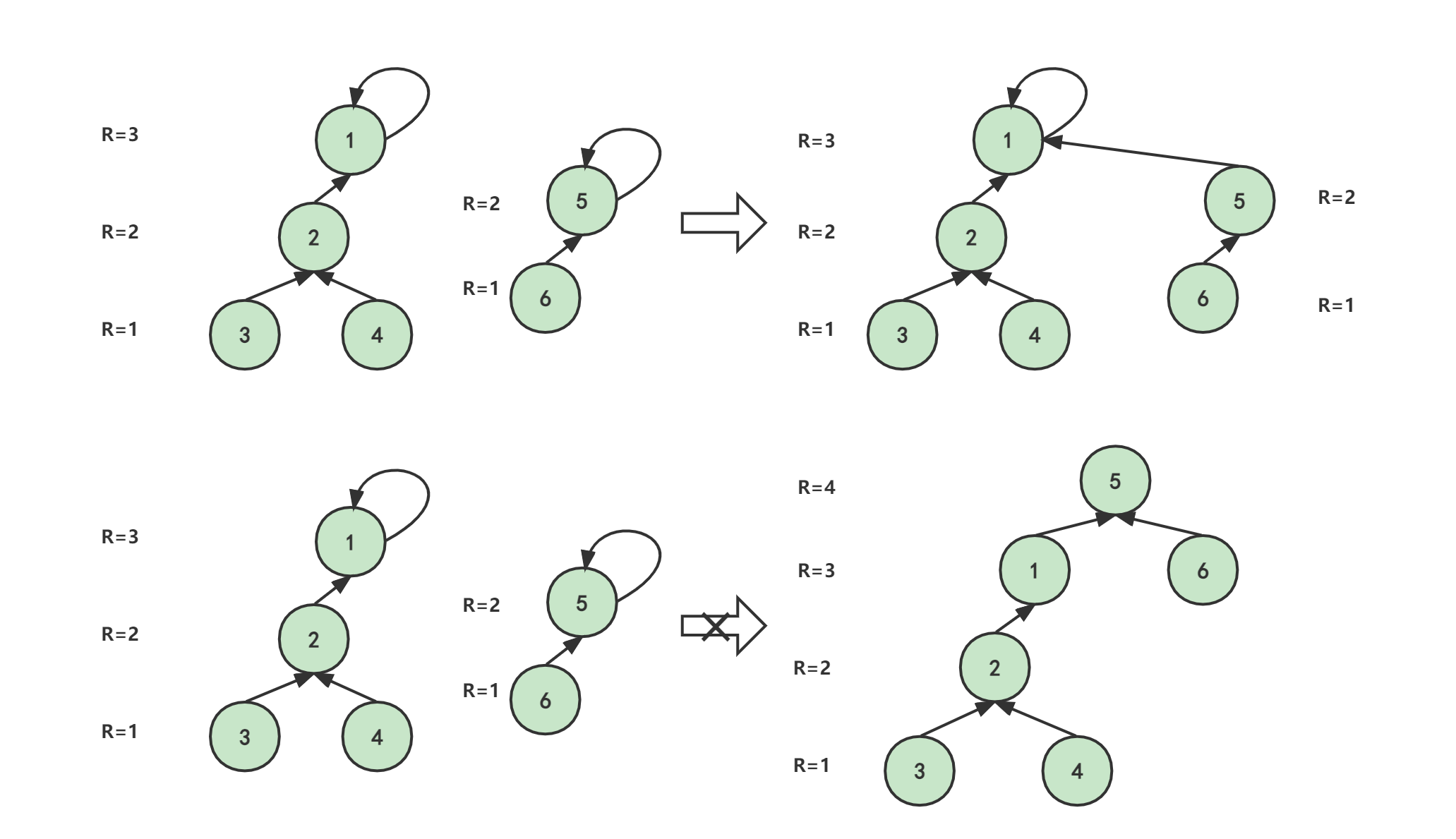
public:UnionFindSet(size_t n){_ufs.resize(n, -1);}//将x2合并到x1void Union(int x1, int x2){assert(x1 < _ufs.size());assert(x2 < _ufs.size());//找到它们的根，然后将其中一个根与另一个根相连int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 != root2){_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}}int FindRoot(int x){assert(x < _ufs.size());while (_ufs[x] >= 0){x = _ufs[x];}return x;}//获取有几个集合，也就是根的数量//根对应的值为负数int GetSize(){int n = 0;for (auto& e : _ufs){if (e < 0){n++;}}return n;}
private:vector<int> _ufs;
};

使用节点实现：

template<class V>
class Node
{
public:Node(V v):value(v){}
private:V value;
};//用链表实现的并查集
template<class V>
class UnionFindNodeSet
{
public:UnionFindNodeSet(vector<V>values){for (auto& value : values){Node<V>* node=new Node<V>(value);nodes.insert(make_pair(value, node));parents.insert(make_pair(node, node));sizeMap.insert(make_pair(node, 1));}}//从cur一直往上找最顶上的父节点//同时把路径上的点都与该父节点相连//为了减少下次查找的路径Node<V>* findFather(Node<V>* cur){//记录路径查找的路径stack<Node<V>*>path;while (cur != parents[cur]){path.push(cur);cur = parents[cur];}//找到头结点,将路径上的节点插到头结点下面while (!path.empty()){Node<V>* ret = path.top();path.pop();parents.insert(make_pair(ret, cur));}return cur;}bool isSameSet(V a, V b){if (!nodes.count(a) || !nodes.count(b)){return false;}return findFather(nodes[a])==findFather(nodes[b]);}void Union(V a, V b){if (!nodes.count(a) || !nodes.count(b)){return ;}Node<V>*aHead = findFather(nodes[a]);Node<V>*bHead = findFather(nodes[b]);if (aHead != bHead){int aSetSize = sizeMap[aHead];int bSetSize = sizeMap[bHead];Node<V>*bigNode = aSetSize >= bSetSize ? aHead : bHead;Node<V>*smallNode = bigNode == aHead?bHead : aHead;parents[smallNode]=bigNode;sizeMap[bigNode] = aSetSize + bSetSize;sizeMap.erase(smallNode);}}//获取有几个集合，也就是根的数量//在parents，其映射为自己int GetSize(){int n = 0;auto it = parents.begin();while(it!=parents.end()){if (it->first==it->second){n++;}it++;}return n;}private://映射当前值和对应的节点map<V, Node<V>*>nodes;//映射node和其父节点map<Node<V>*, Node<V>*>parents;//记录当前节点对应集合中节点的个数map<Node<V>*, int>sizeMap;
};

---

并查集的典型应用

省份数量
相连的省份他们都在一个集合里，所以只需要用并查集统计一共有几个集合即可。

class UnionFindSet
{
public:UnionFindSet(size_t n){_ufs.resize(n, -1);}//将x2合并到x1void Union(int x1, int x2){assert(x1 < _ufs.size());assert(x2 < _ufs.size());int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 != root2){_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}}int FindRoot(int x){assert(x < _ufs.size());while (_ufs[x] >= 0){x = _ufs[x];}return x;}int GetSize(){int n=0;for(auto&e:_ufs){if(e<0){n++;}}return n;}
private:vector<int> _ufs;
};
class Solution {
public:int findCircleNum(vector<vector<int>>& isConnected) {UnionFindSet ufs(isConnected.size());for(int i=0;i<isConnected.size();i++){for(int j=0;j<isConnected.size();j++){if(isConnected[i][j]==1){ufs.Union(i,j);}}}return ufs.GetSize();}
};

等式方程的可满足性
如果两个字符相等，则放入同一个集合之中。
如果两个字符不相等，它们应当在不同的集合中，此时查找它们所在集合的根，如果相同则说明这两个字符在同一个集合中，返回false。

class UnionFindSet
{
public:UnionFindSet(size_t n){_ufs.resize(n, -1);}//将x2合并到x1void Union(int x1, int x2){assert(x1 < _ufs.size());assert(x2 < _ufs.size());int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 != root2){_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}}int FindRoot(int x){assert(x < _ufs.size());while (_ufs[x] >= 0){x = _ufs[x];}return x;}
private:vector<int> _ufs;
};
class Solution {
public:bool equationsPossible(vector<string>& equations) {UnionFindSet ufs(26);//第一遍先把相等的值合并到一个集合for(auto& str:equations){if(str[1]=='='){ufs.Union(str[0]-'a',str[3]-'a');}}//第二遍把不相等的值判断在不在一个集合，如果在就逻辑相悖，返回falsefor(auto& str:equations){if(str[1]=='!'){if(ufs.FindRoot(str[0]-'a')==ufs.FindRoot(str[3]-'a')){return false;}}}return true;}
};