介绍：

并查集属于数据结构的一种是高等数据结构最基础的一部分，主要分为普通并查集种类并查集以及带权并查集。它是一种用于管理元素所属集合的数据结构，这里的集合我们可以理解为一颗数每个元素都是树上的有一个分叉，顺着分叉我们可以找到这棵树的根也就是这个集合里所有元素的“祖先”。

主要操作：

查找（find）：用于查找每棵树的根也就是这个集合所有元素的祖先这样就可以判断两个元素是否属于一个集合就是看两个元素的祖先是否相同。

合并（merge）：用于合并两颗树，将两个集合合并。

求大小（size）：可以统计每个集合元素的个数。

底层实现&代码：

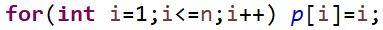
首先我们需要一个数组p 来表示每个元素的父亲例如p[1]：表示1这个元素的根；由于初始时每个元素属于一个独立的整体因此我们要交p[i]利用for 循环初始化令p[i]=i；这样元素本身就是自己的父亲。

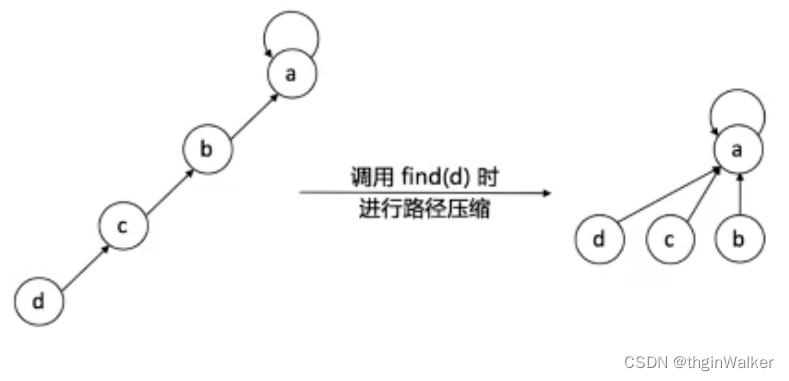
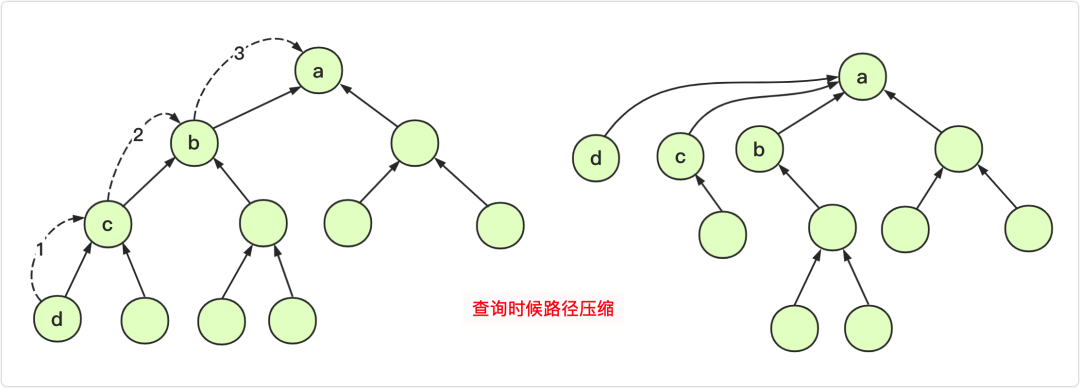
find 函数用来查找每课树的根这里我们规定了根元素的根是他本身因此我们利用递归的思想顺着枝蔓找根并且我们在递归中把每个元素的父亲都设置成了这棵树的根；如图所示：

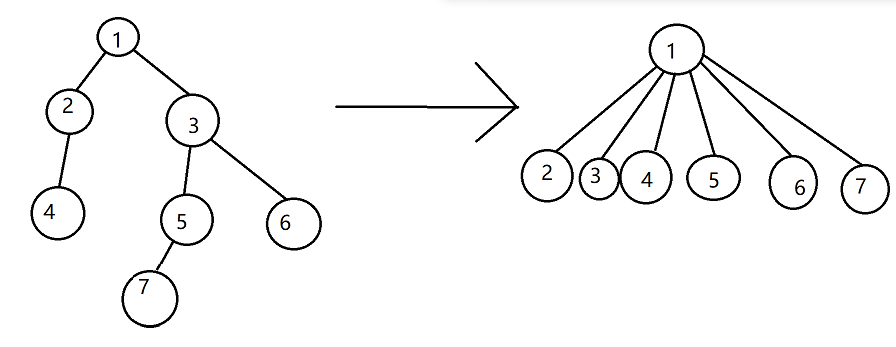
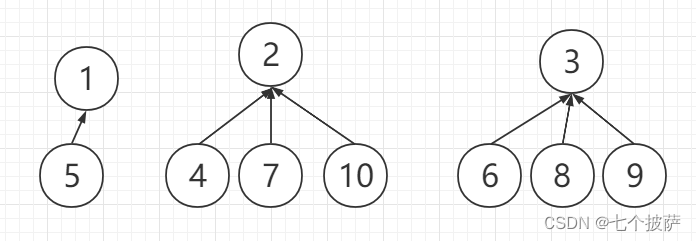
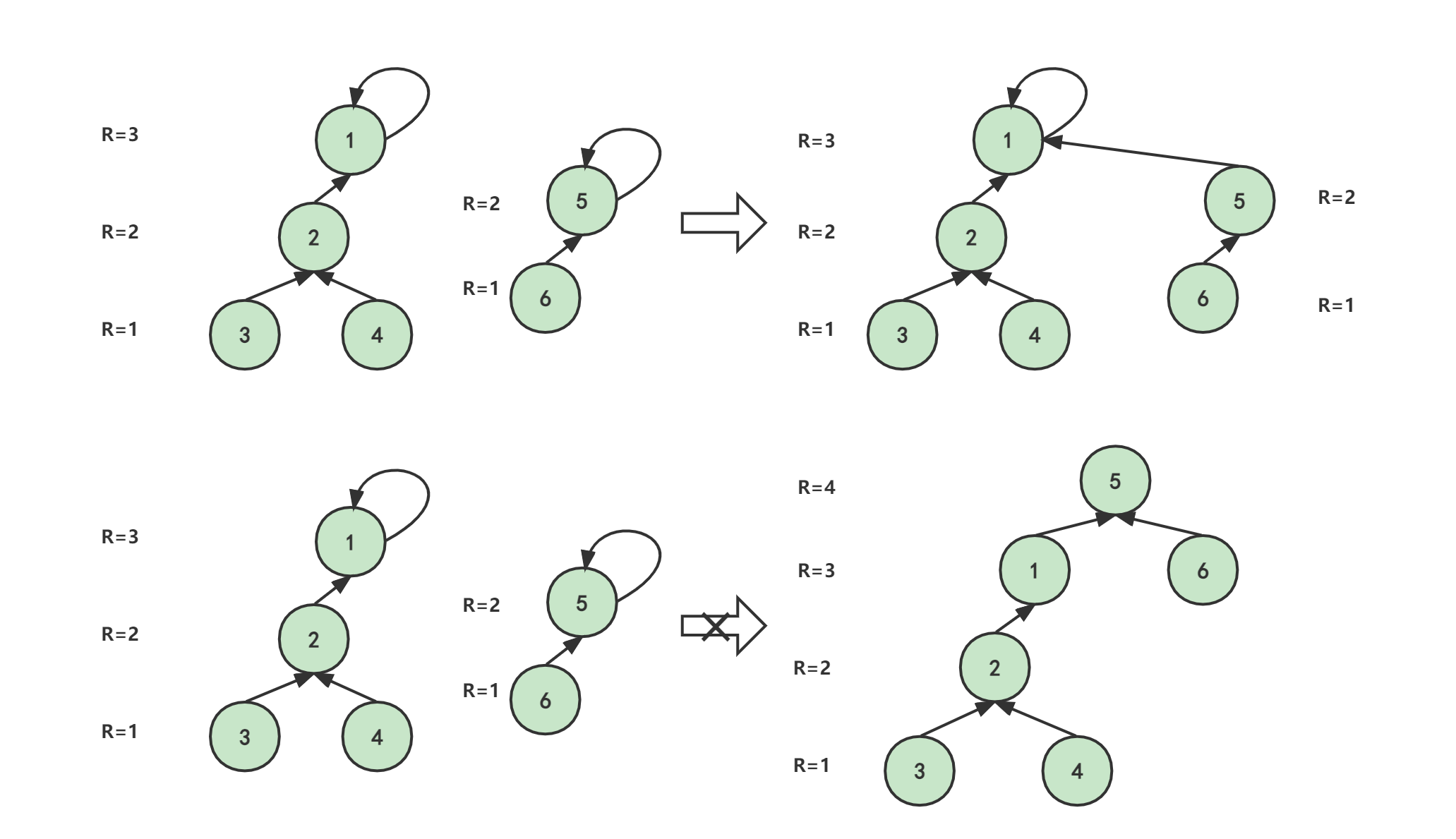
merge函数用来合并两棵树所谓合并我们可以简单的理解为将树上的任意两个树枝连接起来；

这里我们直接将一颗树的根连接在另一颗树上；

例题1（蓝桥杯-#蓝桥幼儿园）

形如：朋友的朋友就是朋友敌人的敌人是朋友这样的字眼或者语义我们就应该首先想到并查集这个数据结构；

题目描述

蓝桥幼儿园的学生是如此的天真无邪，以至于对他们来说，朋友的朋友就是自己的朋友。

小明是蓝桥幼儿园的老师，这天他决定为学生们举办一个交友活动，活动规则如下：

小明会用红绳连接两名学生，被连中的两个学生将成为朋友。

小明想让所有学生都互相成为朋友，但是蓝桥幼儿园的学生实在太多了，他无法用肉眼判断某两个学生是否为朋友。于是他起来了作为编程大师的你，请你帮忙写程序判断某两个学生是否为朋友（默认自己和自己也是朋友）。

输入描述

输出描述

输入输出样例

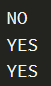
题意理解

首先我们可以从题目中得到朋友的朋友也是朋友的字眼题目中的红绳我们就可以理解为并查集中的树枝连接着每个元素那么这些元素都同属于一棵树也就可以理解为题目中的都是朋友的概念；前面已经介绍了find merge 函数那么这题就迎刃而解了；

AC代码

//普通并查集 注意find函数 一个集相当于一棵树 一堆树组成一片森林 一棵树上有许多果子 find 函数用于找到这颗果子的根
import java.util.Scanner;//朋友的朋友就是我的朋友
public class Programming35_binghchaji {static int N=200010;static int[] p=new int[N];//代表这个数字的根public static void main(String[] args) {Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();for(int i=1;i<=n;i++) p[i]=i;for(int i=0;i<m;i++){int num=in.nextInt();int f1=in.nextInt();int f2=in.nextInt();if(num==1){merge(f1,f2);}else{if(find(f1)==find(f2)) System.out.println("YES");elseSystem.out.println("NO");}}}static int find(int x){if(p[x] != x) p[x]=find(p[x]);return p[x];}static void merge(int x,int y){x=find(p[x]);y=find(p[y]);p[x]=y;//合并两棵树}
}

例题2（蓝桥杯 #蓝桥侦探）

题目描述

输入描述

输出描述

输入输出样例

题意理解&解题思想

例题1 是最基础的普通并查集本题是种类并查集与例题一不同的是我们可以从本题的字眼中得到敌人的敌人是朋友意思是一个与我不在一个大厅的大臣A说另一个大臣B与他不在一个大厅那么照他所说大臣B必定与我一个在同一个大厅中这种并查集我们不能简单的只开一个长度为N的数组了我们要开一个长度为2*N的数组那么多出来的i+N就用来表示i的对立面；

AC代码

package lanqiao.practice;//种类并查集 敌人的敌人是朋友 普通并查集做不到
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Programming36_binghchaji_2 {static int N=500010;static int M=500010;static int[] q=new int[2*N+10];public static void main(String[] args) throws IOException {BufferedReader br=new BufferedReader(new InputStreamReader(System.in));String[] s=br.readLine().split(" ");int n=Integer.parseInt(s[0]);int m=Integer.parseInt(s[1]);for(int i=1;i<=n*2;i++)q[i]=i;for(int i=0;i<m;i++){s=br.readLine().split(" ");int x=Integer.parseInt(s[0]);int y=Integer.parseInt(s[1]);if(find(x)!=find(y)){merge(x,y+n);merge(y,x+n);}else {System.out.println(x);break;}}}static int find(int x){if(q[x]!=x) q[x]=find(q[x]);return q[x];}static void merge(int x,int y){x=find(q[x]);y=find(q[y]);q[x]=y;}
}

例题3（蓝桥杯 #蓝桥部队）

题目描述

输入描述

输出描述

对于每个询问，输出一行表示答案；

输入输出样例

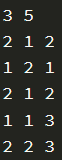
题意理解&解题思想

本题与上两题不同的是本题多了几个要素一个是要另外设置一个函数判断是否属于同一队列那么就相当于判断两个元素是否在同一颗树上另外一个要素就是要计算两个士兵之间的距离那么我们可以理解为计算一棵树上两个果实之间的距离我们这里设置一个新的数组d 来表示元素[i]到根的距离 siz 来表示一棵树元素的多少那么我们在合并元素的时候要注意元素到根的距离会发生改变；这种并查集属于带权并查集

AC代码

package lanqiao.practice;//带权并查集
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Programming37_bingchaji_3 {public static void main(String[] args) throws IOException {BufferedReader br=new BufferedReader(new InputStreamReader(System.in));String[] s=br.readLine().split(" ");int n=Integer.parseInt(s[0]);int m=Integer.parseInt(s[1]);UF uf=new UF(n+10);for(int i=0;i<m;i++){s=br.readLine().split(" ");int op=Integer.parseInt(s[0]);int x=Integer.parseInt(s[1]);int y=Integer.parseInt(s[2]);if(op==1){uf.merge(y, x);}elseSystem.out.println(uf.dist(x, y));}}
}
//打包并查集class UF{int[] f,d,siz;//f用来统计一个数字的根 d用来统计siz用来统计这颗树的果zhi的多少public UF(int n){f=new int[n];d=new int[n];siz=new int[n];for(int i=1;i<n;i++)f[i]=i;Arrays.fill(siz,1);//初始时每棵树就根这一个元素；}int find(int x){if(x==f[x]) return f[x];int root =find(f[x]);d[x]+=d[f[x]];return f[x]=root;}boolean same(int x,int y){return find(x)==find(y);}boolean merge(int x,int y){x=find(x);y=find(y);if(x==y) return false;     d[y]+=siz[x];siz[x]+=siz[y];f[y]=x;return true;}int size(int x){return siz[find(x)];}int dist(int x,int y){if(!same(x,y)) return -1;return Math.abs(d[x]-d[y])-1;}}

总结

其实并查集难就难在要有一双发现并查集的眼睛很多题目是不容易看出要用并查集来解决的；

并查集的代码可以打包成一个模板以后我们发现要用到并查集的时候就可以直接套用模板，

实例化对象来调用函数。

打包代码

//打包并查集class UF{int[] f,d,siz;//f用来统计一个数字的根 d用来统计siz用来统计这颗树的果子的多少public UF(int n){f=new int[n];d=new int[n];siz=new int[n];for(int i=1;i<n;i++)f[i]=i;Arrays.fill(siz,1);//初始时每棵树就根这一个元素；}int find(int x){if(x==f[x]) return f[x];int root =find(f[x]);d[x]+=d[f[x]];return f[x]=root;}boolean same(int x,int y){return find(x)==find(y);}boolean merge(int x,int y){x=find(x);y=find(y);if(x==y) return false;     d[y]+=siz[x];siz[x]+=siz[y];f[y]=x;return true;}int size(int x){return siz[find(x)];}int dist(int x,int y){if(!same(x,y)) return -1;return Math.abs(d[x]-d[y])-1;}