本文是关于一个虚构的对象，称为带一个元素的域，有时表示为F_un。F表示域，而“un”表示1。当我第一次听说这个的时候，我以为这是一个笑话。对象是“Fun”，它并不存在。

但是很多伟大的数学家已经在这方面做了很多研究，如雅克·提茨(Jacques Tits)，阿兰·康尼斯(Alain Connes)，尤里·曼宁(Yuri Manin)等等。

一个精妙的公式可能会对数学的多个分支产生重大影响，包括计算复杂性理论、非交换几何学和代数数论等。

本文将集中讨论为什么它可能对黎曼猜想有所帮助。让我们开始吧。

域是什么？

域是数学的基本对象之一。域是一个具有两个操作(加法和乘法)的集合，其中有一个加法的单位(0)和一个乘法的单位(1)，每个元素(除了0)对这两个操作都有一个逆。

域有很多种，其中实数域 最容易理解。每个实数都有一个加法的逆元素。例如，3的加性逆元素是-3，因为3+(-3)=0。每一个非零实数都有一个乘法的逆元素。例如，3的乘法逆元素是(1/3)。这是因为3*(1/3)=1。

同理，有理数集 也是一个域。还有 ，也就是复数(虚数)的集合也是一个域。

并不是所有数字系统都是域。整数集合 不能构成一个域，因为虽然有加法和乘法运算，但3没有乘法逆(1/3不是整数)。

并不是所有的域都是无限的。实际上，带有“mod 3”算术的整数(表示为 /3)是一个包含三个元素的域。

Mod 3算术可以正常的加和乘，然后像时钟一样循环：0，1，2，3 = 0，4 = 1，5 = 2，6 =0，……(负号也可以，-1=2，等等)。

我们可以验证一下：

1 + 2 = 0。这表明1是2的加法逆元素(反之亦然)。

2 * 2 = 4 = 1。这表明2是它自己的乘法逆元素。

这是唯一两个很难验证的数字，所以 /3确实是一个域。

在这一点上，域是很容易理解的。注意到在有限域的情况下会发生一些奇怪的事情。如果你把1和它自己相加3次，你会得到加法恒等式1+1+1=0。但如果你在无限域中这样做，这永远不会发生。

如果将1和它自身相加有限次得到0，相加的次数被称为域的特征。我们用字母p表示。 /3的特征是3。

如果1和它本身相加不管你做多少次都不会得到0，那么这个域的特性就是0。

重要术语：我将在本文中继续提到正的特性。这是表示特征不等于0的标准方法。换句话说， p>0。

大多数关于抽象代数的第一门课程都会证明一个惊人的事实，即在有限域的情况下，这个特征总是一个素数！此外，有限域的元素数总是这个素数的幂，即p (p是这种域的特征)。

相反，对于任何素数幂，都有一个显式的构造，用于包含这么多元素的域。因此，域有2个元素，3个元素，4个元素，5个元素，7，8，9，等等。没有包含6个或10个元素的域。

为了完备起见，并不是所有的无限域都具有0的特征。这种有限的解释很容易让人产生错误的印象。

这给我们带来了一个关键问题，没有一个域只有一个元素！(也就是说，1不是素数幂)。

在深入讨论这个问题之前，让我们先绕个圈子，看看为什么有人会希望有这样一个东西。

有限域上的黎曼假设

这才是真正酷的地方。

事实证明，在正特征域上“做几何”通常比在0特征上更容易。我就不细说原因了。

因此，有时这是一个很好的工具，你可以把你想要证明的东西通过 简化为正的特性，在那里证明它，然后试图以某种方式把它提升到0特征(这实际上是本文的一个主要观点)。

要定义几何在正特性中的含义有点复杂，但我们可以依靠一个相当准确的类比。 或 上的几何只是研究由多项式的零集形成的形状。

所以，如果在 上，有两个变量，一个多项式p(x，y)=y-x ，当它等于0时，你得到的几何图形就是抛物线：

x = 0

或者大家更熟悉的y=x ：

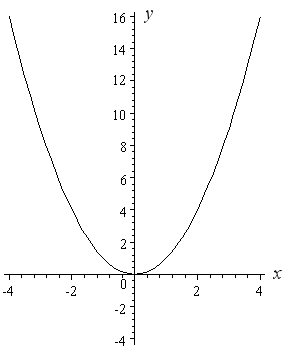
后续我将在另外两篇文章中讨论 上的其他理论(霍奇猜想、法尔廷斯定理和莫德尔猜想猜想)。

当你在 上这样做时，你会发现拓扑结构和整数解的数量(费马最后定理等)之间有一个有趣的相互作用。

我们可以在有限域上做同样的事情。域 /3上的多项式p(x，y)=y-x 的几何形式来自于代入并检查零集。它更难想象成“几何图形”，但实际上更容易处理，因为它是有限的。

实际上，我们可以确定{(0，0)，(1，1)，(2，1)}是仅有的三个点。我省略了一些重要的细节，但这种思考方式对于获取要点来说已经足够好了。

ζ函数(Zeta Functions)

假设我们从一个有限域开始，该域上有p个元素，比如F，和一条“曲线”C(为简单起见，多项式的零集)。

我们可以计算C的点数，N(1)。

然后我们可以在有p^2元素的域上看同样的方程，把它叫做N(2)等等。

所以N是一个函数。N(k)就是C在有p^k个元素的域上的点数。

下一部分看起来很复杂，但它会大大简化。

考虑到函数：

C的局部ζ函数定义为：

这可能看起来很疯狂，但我们可以通过一个例子很容易地看出，定义的构造是为了消去和简化。

如果我们从多项式p(x)=x开始，那么任意域上x=0的唯一解就是x=0。

无论我们检查多少个域，都只有一个点。因此，对于所有k, N(k)=1。

让我们代入：

因此：

韦尔猜想是由安德烈·韦尔(André Weil)在1949年提出的关于任意X(不只是曲线或点，也包括高维空间)的Z(X，t)猜想。从那时起，他们一直是代数和算术几何研究的主要驱动力之一。

数学家们用了几十年的时间证明了它们，并且发现了许多现代的替代证明。关键的结论是，韦尔猜想之一就是这些函数的“黎曼猜想”。韦尔自己证明了有限域上曲线的黎曼猜想。

通过适当的几何机制，证明是相对容易的。

只有一个元素的域

我们终于准备好讨论只有一个元素的域了。

记住，它不存在。

但我们的想法是建立一些东西让我们可以做一种广义几何。思考一下 ，它的性质是“减少mod p”，对于任何素数p都会给我们一个有p个元素的域(这是我们之前定义有p个元素的域的方式)。

这个事实可以用几何的方法来重新表述。有一个几何空间，X=Spec( )，所以，对于每个质数p，减少mod p得到有p个元素的域上的1个点，F 。

我们已经算出了一个点的局部ζ函数，它是1 / (1 - t)。

但是我们通过减少mod p来得到一个局部的ζ函数。当你将这些结合在一起得到X的“全局”ζ函数时，正确的方法是相乘并追踪素数 (tp )，我们可以得到：

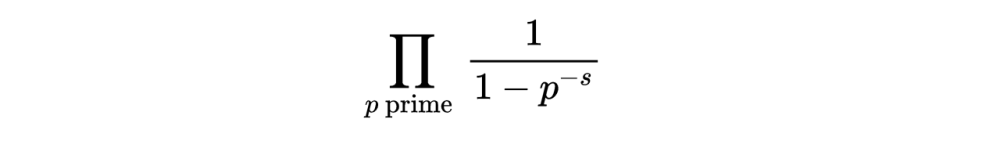
黎曼ζ函数的乘积形式。这就是我们一直在找的东西。

如果有一个叫做F_un的东西,它的作用就像一个有限域，我们可以把X=Spec( )当做它上面的一条曲线然后，用韦尔定理来证明黎曼猜想。

数学家们在这方面已经做了一些非常了不起的工作。也许有一天我们会有一个证明黎曼猜想的Fun。