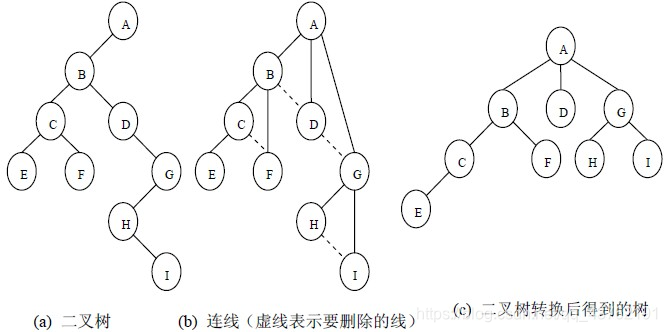
实际测试中，如果输入条件较多，再加上各种输人与输出之间相互的作用关系，画出的因果图会比较复杂，容易使人混乱。为了避免这种情况，人们往往使用决策表法代替因果图法。

决策表也称为判定表，其实质就是一严逻辑农。在在序攻计发股初期，判定表就已经被当作程序开发的辅助工具，帮助开发人员整埋开反模式和沉程，因为它可以把复杂的逻辑关系和多种条件组合的情况表达得既具体又明确。利用决策表可以设计出完整的测试用例集合。

为了让大家明白什么是决策表，下面通过一个“图书阅读指南”来制作一个决策表。图一无书阅读指南指明了图书阅读过程中可能出现的状况，以及针对各种情况给读者的建议。在图书阅读过程中可能会出现3种情况：是否疲倦、是否对内容感兴趣、对书中的内容是否感到糊涂。如果回答是肯定N，针对这8种组合，阅读指南给读看促制作的阅读指南决策表这3种情况可以有23=8种组合、针对这8种组合，阅读指南给读者提供了4条建议：回到本章开头重读、继续读下去、跳到下一章去读、停止阅读并休息，据此制作的阅读指南决策表下表所示。

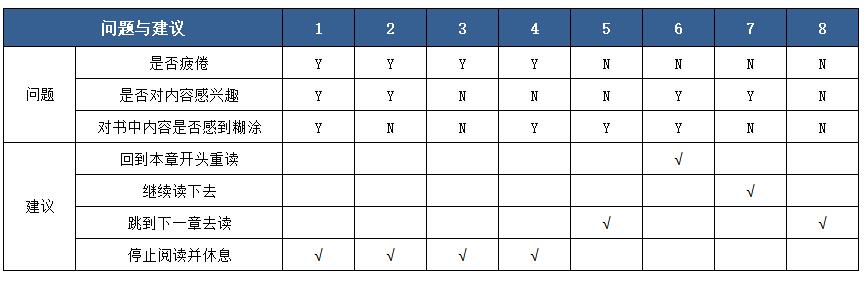
表1

上表就是一个决策表，根据这个决策表阅读图书，对各种情况的处理一目了然，简洁高效。

决策表通常由4个部分组成，具体如下。

(1)条件桩：列出问题的所有条件,除了某些问题对条件的先后次序有要求之外,通常决策表中所列条件的先后次序都无关紧要。

(2)条件项：条件项就是条件桩的所有可能取值。

(3)动作桩：动作桩就是问题可能采取的操作，这些操作一般没有先后次序之分。

(4)动作项：指出在条件项的各组取值情况下应采取的动作。

这4个组成部分对应到表1中，条件桩包括是否疲倦、是否对内容感兴趣、对书中内容是否感到糊涂；条件项包括“Y”与“N”；动作桩包括回到本章开头重读、继续读下去、跳到下一章去读、停止阅读并休息;动作项是指在问题综合情况下所采取的具体动作，动作项与条件项紧密相关，它的值取决于条件项的各组取值情况。

在决策表中，任何一个条件组合的特定取值及其相应要执行的操作称为一条规则，即决策表中的每一列就是一条规则，每一列都可以设计一个测试用例，根据决策表设计测试用例就不会有所遗漏。

在实际测试中，条件桩往往很多，而且每个条件桩都有真假两个条件项，有n个条件桩的决策表就会有2条规则，如果每条规则都设计一个测试用例，不仅工作量大，而且有些工作量可能是重复且无意义的,例如，在上面表中，第1、2条规则，第1条规则取值为：Y、Y、Y，执行结果为“停止阅读并休息”；第2条规则取值为：Y、Y、N，执行结果也为“停止阅读并休息”。对于这两条规则来说，前两个问题的取值相同,执行结果一样，因此第3个问题的取值对结果并无影响，这个问题就称为无关条件项，使用“-”表示。忽略无关条件项，可以将这两条规则进行合并，如下图所示。

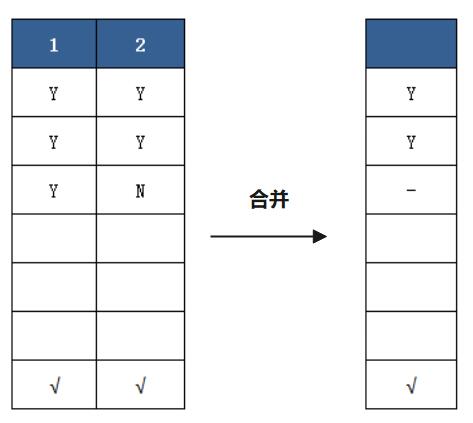
图1 合并规则1与规则2

由图1可知，规则1与规则2合并成了一条规则。由于合并之后的无关条件项(-)包含其他条件项取值,因此具有相同动作的规则还可进一步合并，如图2所示。

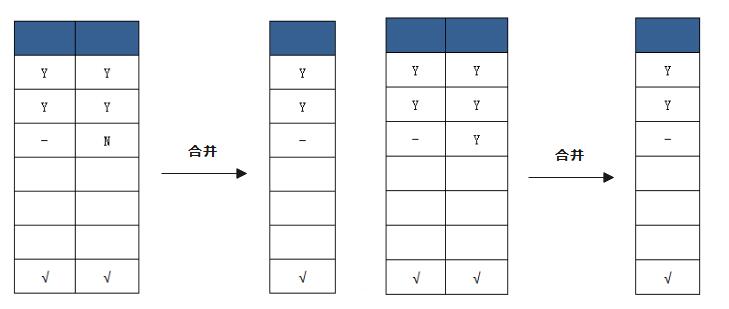
图2 进一步合并规则

将规则进行合并，可以减少重复的规则，相应地减少测试用例的设计，这样可以大大降低软件测试的工作量。图书阅读指南决策表最初有8条规则,进行合并之后,只剩下5条规则，简化后的图书阅读指南决策表如表2所示。

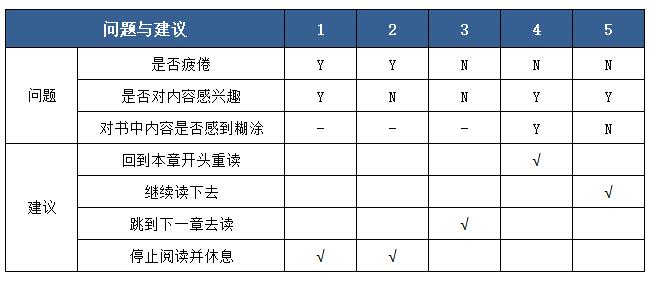
表2是简化后的图书阅读指南决策表，相比于表1，它简洁了很多，在测试时只需要设计5个测试用例即可覆盖所有的情况。

相比于因果图，决策表能够把复杂的问题按各种可能的情况一一列举，简明而易于理解，也避免遗漏，因此在多逻辑条件下执行不同操作的情况，决策表使用的更多。

本文转自：黑马程序员软件测试 http://test.itheima.com