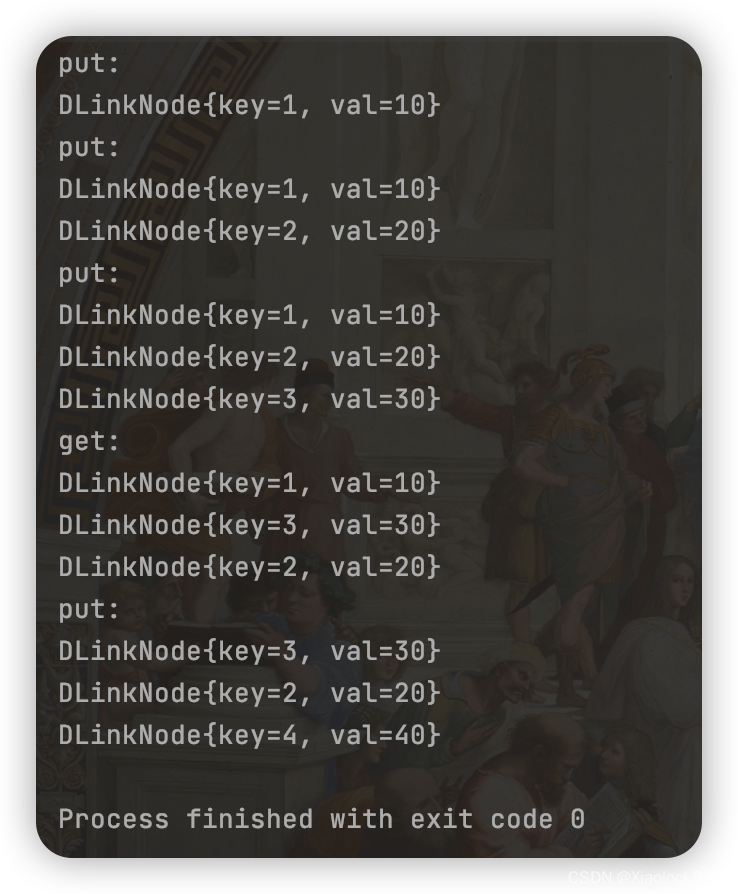
目录
一.二叉搜索树规则
二.框架
三.实现
1.查找, 插入, 删除
迭代法实现
递归法实现
2.构造, 赋值
默认构造
拷贝构造
赋值运算符重载
3.中序遍历
四.时间复杂度及稳定性
五.key模型与key/value模型
1.key模型
2.key/value模型
一.二叉搜索树规则
二叉搜索树又称二叉排序树
二叉搜索树的中序遍历结果是递增的
规则:
一棵二叉树, 可以为空, 如果不为空, 则满足:
1.非空左子树的所有节点的键值小于其根节点的键值
2.非空右子树的所有节点的键值大于其根节点的键值
3.每个左子树都满足规则1, 每个右子树都满足规则2, 即左右子树都是搜索二叉树
4.不会出现重复的键值
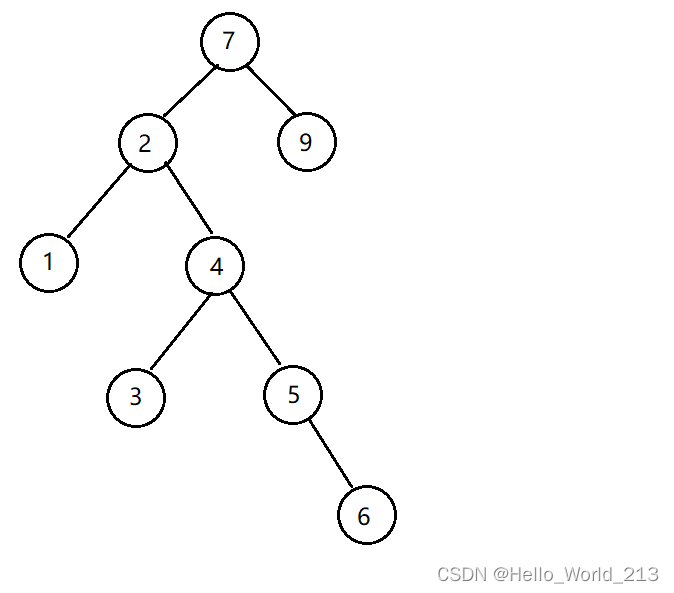
二.框架
采用二叉链
1. 二叉搜索树主要支持增删查等功能, 不支持修改, 因为使用的主要场景是搜索
2. 二叉搜索树自带去掉重复键值的功能, 因为重复键值不会被插入
template<class T>
struct BinaryTreeNode
{BinaryTreeNode* _left;BinaryTreeNode* _right;T _val;BinaryTreeNode(const T& val):_left(nullptr),_right(nullptr),_val(val){}
};template<class T>
class BinarySearchTree
{
public:typedef BinaryTreeNode<T> BTNode;BinarySearchTree();//拷贝构造(前序遍历拷贝)BinarySearchTree(BinarySearchTree& tmp);//赋值运算符重载BinarySearchTree& operator=(BinarySearchTree tmp);//插入(迭代法)bool insert(const T& val);//插入(递归法)bool insertR(const T& val);//中序打印(增序列)void inoder();//查找(迭代法)bool find(const T& val);//查找(递归法)bool findR(const T& val);//删除(迭代法)bool erase(const T& val);//删除(递归法)bool eraseR(const T& val);
private:BTNode* _BinarySearchTreeCopy(BTNode* root);bool _insertR(BTNode*& root, const T& val);bool _findR(BTNode* root, const T& val);bool _eraseR(BTNode*& root, const T& val);void _inoder(BTNode* root);BTNode* _root = nullptr;
};
三.实现
1.查找, 插入, 删除
迭代法实现
查找
bool find(const T& val);
从根节点开始查找, 如果val大于根节点的键值, 去根的右边找; 如果val小于根节点的键值, 去根的左边找
如果最终没找到, 返回false; 如果最终找到了, 返回true
bool find(const T& val)
{BTNode* cur = _root;while (cur){if (cur->_val > val){cur = cur->_left;}else if (cur->_val < val){cur = cur->_right;}else{return true;}}return false;
}插入
bool insert(const T& val);
从根节点开始遍历, 如果要插入的节点比根节点键值大, 遍历根节点的右子树; 如果要插入的节点比根节点键值小, 遍历根节点的左子树
如果遍历到键值与val相等的节点, 则说明该节点的键值已经存在, 不需要插入, 返回false
如果遍历到空节点, 则可以进行插入了, 插入时要注意插入的位置是上一个节点的左还是右, 所以需要记录上一个节点, 同时需要一个if...else判断, 插入之后返回true
注意一个额外情况:
插入之前这是一棵空树, 说明_root为空, 应该单独处理, 否则将会对prev这个空指针进行访问引发崩溃
bool insert(const T& val)
{//new出新节点BTNode* newnode = new BTNode(val);//如果是空树if (_root == nullptr){_root = newnode;return true;}//树不为空BTNode* cur = _root;BTNode* prev = nullptr;while (cur){if (cur->_val > val){prev = cur;cur = cur->_left;}else if (cur->_val < val){prev = cur;cur = cur->_right;}else{return false;}}if (prev->_val < val){prev->_right = newnode;}else if (prev->_val > val){prev->_left = newnode;}return true;
}删除
bool erase(const T& val);
删除是二叉搜索树中最繁杂的一个接口, 很容易出错, 需要额外小心
删除的前半部分思想与查找相同, 也需要记录待删除节点的上一个节点
当找到要删除的节点之后, 开始删除
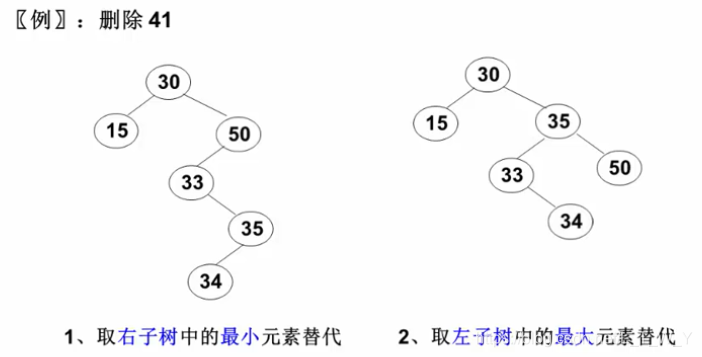
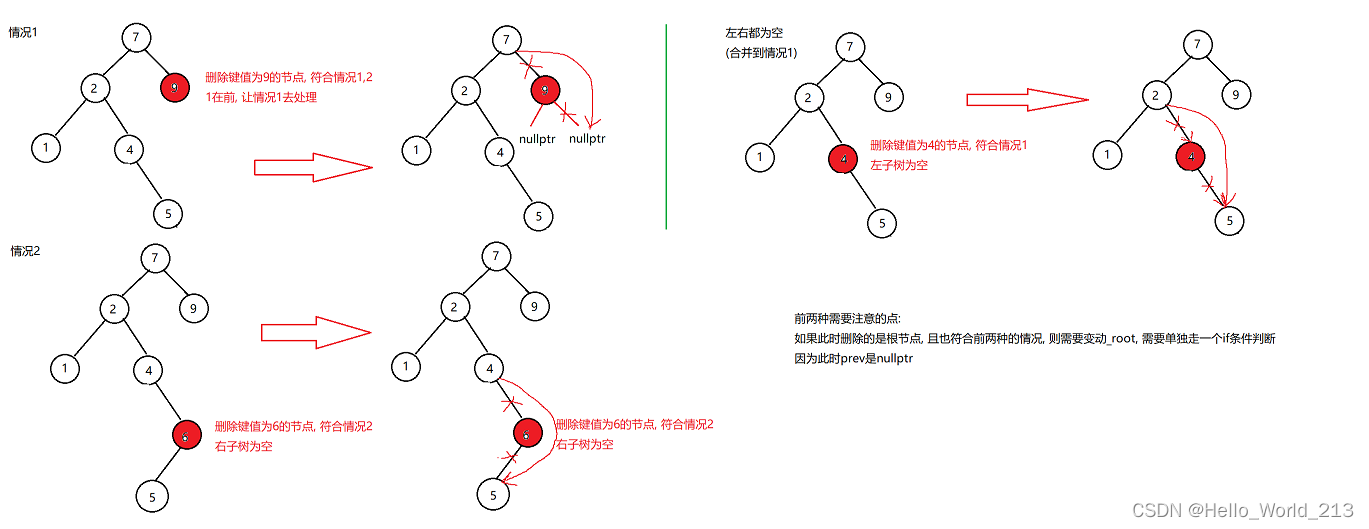
删除分为四种情况:
1.待删除节点的左右子树都为空
2.待删除节点的左子树为空
3.待删除节点的右子树为空
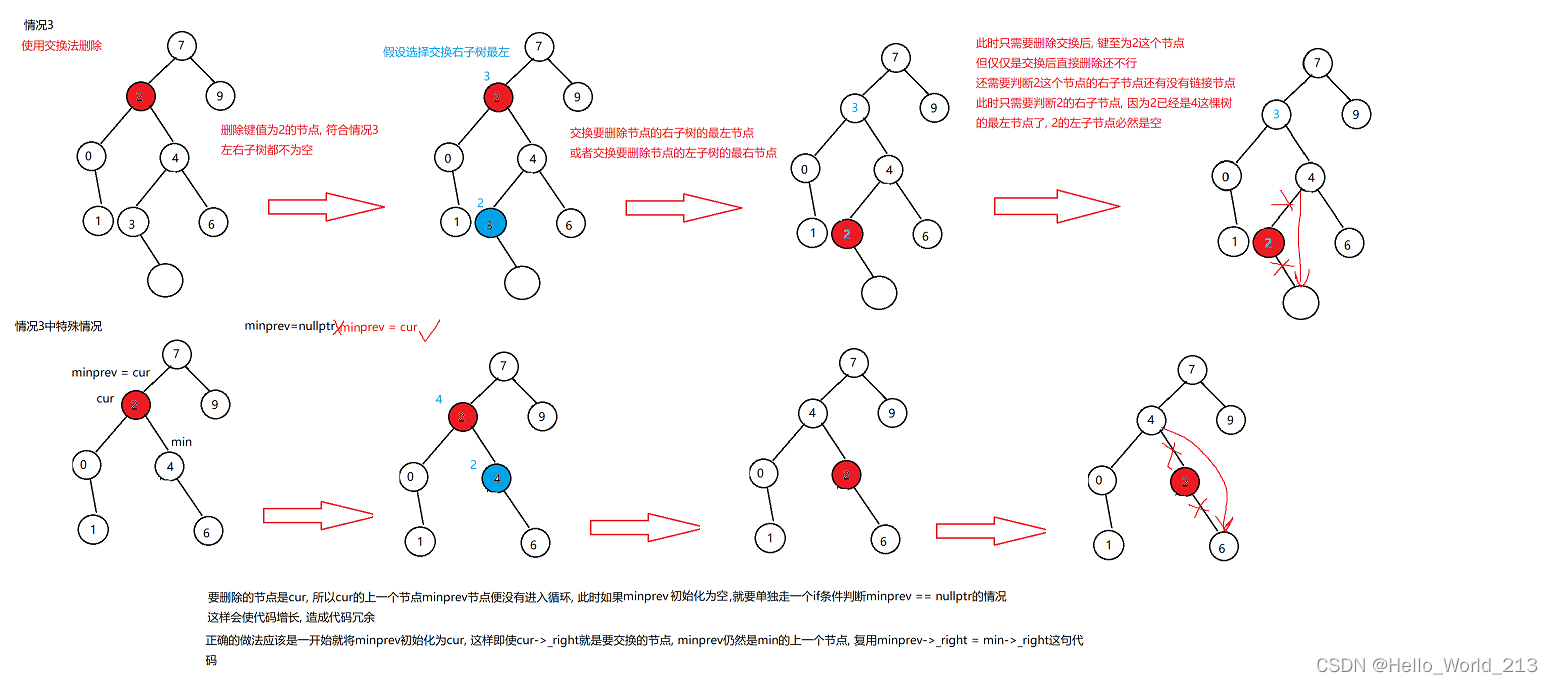
4.待删除节点的左右子树都不为空
情况1可以归类到情况2, 左右都为空认为是左为空右不为空去处理, 最终prev链接右不为空节点, 但实际链接的是空节点
将1归类到2之后, 大体分为三种情况
1.左子树为空
2.右子树为空
3.左右子树都为空
bool erase(const T& val)
{BTNode* cur = _root;BTNode* prev = nullptr;while (cur){if (cur->_val > val){prev = cur;cur = cur->_left;}else if (cur->_val < val){prev = cur;cur = cur->_right;}else{//开始删除if (cur->_left == nullptr)//左为空{if (prev == nullptr)//删除根节点_root = cur->_right;else{if (prev->_val < val)prev->_right = cur->_right;elseprev->_left = cur->_right;}delete cur;}else if(cur->_right == nullptr)//右为空{if (prev == nullptr)//删除根节点_root = cur->_left;else{if (prev->_val < val)prev->_right = cur->_left;elseprev->_left = cur->_left;}delete cur;}else//左右都不为空{//交换法删除, 交换cur和cur右子树的最小节点BTNode* minPrev = cur;//这里需要注意BTNode* min = cur->_right;while (min->_left){minPrev = min;min = min->_left;}swap(cur->_val, min->_val);if (min == minPrev->_left)minPrev->_left = min->_right;else//min == minPrev->_rightminPrev->_right = min->_right;delete min;}return true;}}return false;
}递归法实现
在思想上: 与迭代法一致
在写代码的角度: 与迭代法相比, 非常简洁, 可读性更强
由于每次接收参数以BTNode*& root的方式去接收, 即可不用进行繁杂的左右判断
插入则直接new出节点赋值给root即可
删除则直接赋值root = root->_right或者root = root->_left(1,2的情况)
情况3直接复用_eraseR即可复用到情况1(左为空), 最终也是走了一个root = root->right
对于删除节点是根节点也不需要单独做处理
查找
bool findR(const T& val)
{return _findR(_root, val);
}bool _findR(BTNode* root, const T& val)
{if (root == nullptr){return false;}if (root->_val < val){return _findR(root->_right, val);}else if (root->_val > val){return _findR(root->_left, val);}else{return true;}
}插入
bool insertR(const T& val)
{return _insertR(_root, val);
}bool _insertR(BTNode*& root, const T& val)
{if (root == nullptr){root = new BTNode(val);return true;}if (root->_val > val){return _insertR(root->_left, val);}else if (root->_val < val){return _insertR(root->_right, val);}else{return false;}
}删除
bool eraseR(const T& val)
{return _eraseR(_root, val);
}bool _eraseR(BTNode*& root, const T& val)
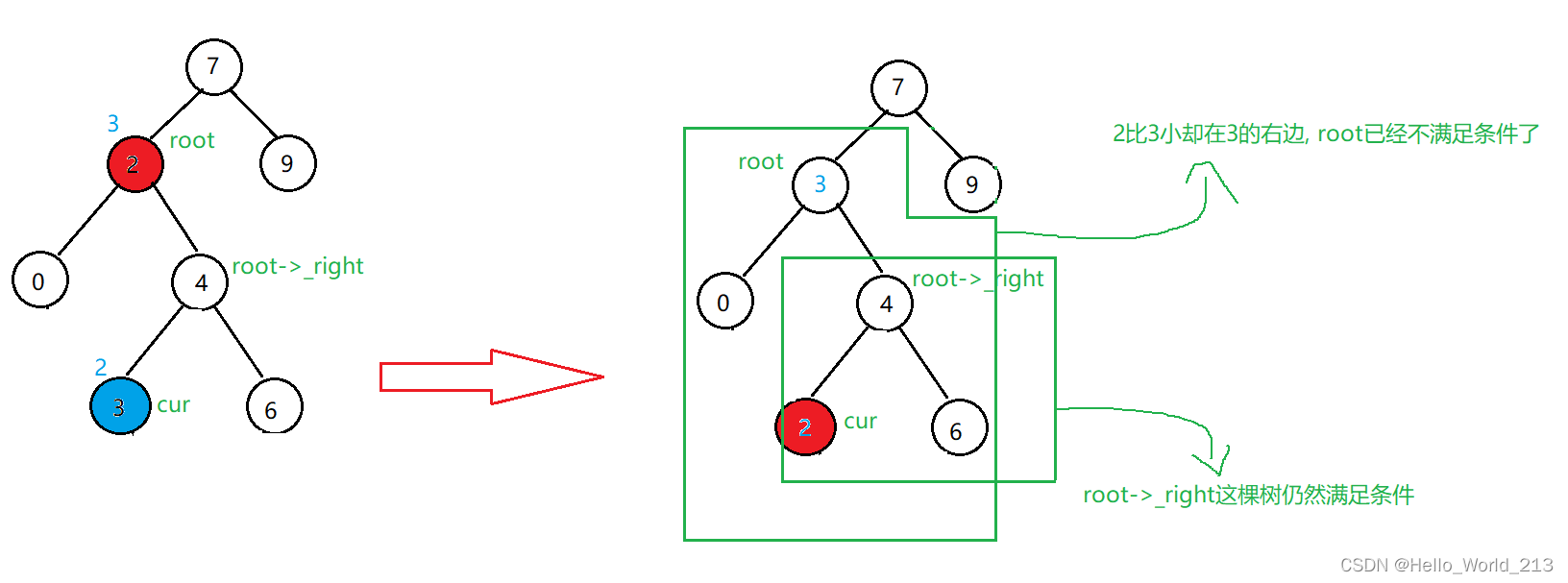
{if (root == nullptr){return false;}if (root->_val > val){return _eraseR(root->_left, val);}else if (root->_val < val){return _eraseR(root->_right, val);}else{//开始删除if (root->_left == nullptr){BTNode* cur = root;root = root->_right;delete cur;return true;}else if (root->_right == nullptr){BTNode* cur = root;root = root->_left;delete cur;return true;}else{BTNode* cur = root->_right;while (cur->_left){cur = cur->_left;}swap(cur->_val, root->_val);//注意对_eraseR复用时传参一定是root->_right, 因为此时已经交换了节点//交换了节点, 对于root而言, 删除掉节点前, root不再是一棵二叉搜索树//而交换对root->_right没有影响, 以root->_right为根节点的子树仍是一棵二叉搜索树return _eraseR(root->_right, cur->_val);}}
}
2.构造, 赋值
默认构造
采用C++11的新写法
注意: 这种写法通常用于, 我们显示的写了其他构造函数, 编译器就不会自动生成默认构造了, 这时需要我们手动去写默认构造, C++11提供了这种便捷的方式, 但是有一点需要注意的是, 如果你再使用默认构造实例化对象时如果不在成员变量声明处加缺省值, 会导致初始化的成员变量是随机值, 所以Node* _root = nullptr必须这样声明成员变量
BinarySearchTree() = default;
拷贝构造
拷贝构造的参数必须写成引用, 避免死循环
使用递归遍历依次拷贝
注意: 对于二叉搜索树而言, 插入的顺序不同, 构建出的二叉搜索树的形状就不同
所以我们在拷贝时, 必须严格遵守原树的形状去拷贝
绝不可以先遍历再依次插入, 必须在遍历的同时进行构建, 且这里必须使用前序遍历
BinarySearchTree(BinarySearchTree& tmp)
{_root = _BinarySearchTreeCopy(tmp._root);
}BTNode* _BinarySearchTreeCopy(BTNode* root)
{if (root == nullptr){return nullptr;}BTNode* copynode = new BTNode(root->_val);copynode->_left = _BinarySearchTreeCopy(root->_left);copynode->_right = _BinarySearchTreeCopy(root->_right);return copynode;
}
赋值运算符重载
复用拷贝构造
BinarySearchTree& operator=(BinarySearchTree tmp)
{swap(tmp._root, _root);return *this;
}3.中序遍历
void inoder()
{_inoder(this->_root);cout << endl;
}void _inoder(BTNode* root)
{if (root != nullptr){_inoder(root->_left);cout << root->_val << ' ';_inoder(root->_right);}
}四.时间复杂度及稳定性
二叉搜索树是一种极其不稳定的数据结构
二叉搜索树的插入与删除都是在查找基础之上的操作, 所以它的查找效率代表了二叉搜索树的整体性能
查找效率:
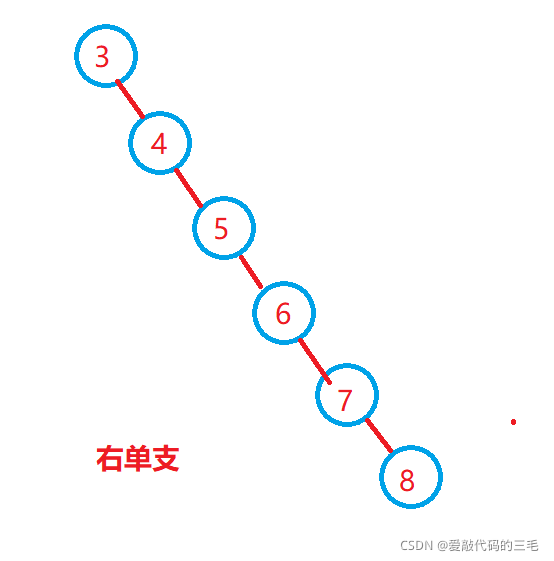
时间复杂度是O(h) -- h是树的高度
最优查找效率: O(logN) -- 与完全二叉树非常类似
最坏查找效率: O(N) -- 单枝树
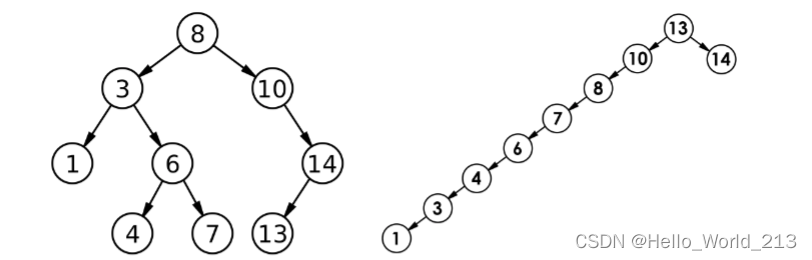
因为二叉搜索树的高度不定, 所以使其非常不稳定
五.key模型与key/value模型
1.key模型
key模型: 查找某个值在不在的场景, key不可被修改
2.key/value模型
key/value模型: 查找且匹配的场景, 根据key(键值)找到value, key不可被修改, value可以被修改