二叉搜索树

一、什么是二叉搜索树

二叉搜索树（BST，Binary Search Tree），也称二叉排序树或二叉查找树。
二叉搜索树：一棵二叉树，可以为空；如果不为空，满足以下性质：

非空左子树的所有键值小于其根结点的键值。
非空右子树的所有键值大于其根结点的键值。
左、右子树都是二叉搜索树。

下图是几个例子：
在这里插入图片描述
上图值为10的结点的右子树为7，比10小，不满足条件2，所以这棵树不是二叉搜索树。

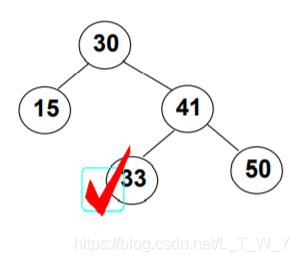
在这里插入图片描述
上图各个结点都满足条件，所以这棵树是二叉搜索树。

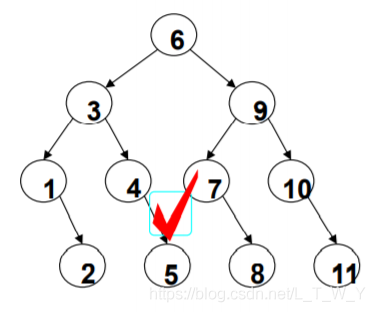
在这里插入图片描述
上图各个结点都满足条件，所以这棵树也是二叉搜索树。

看完上面的介绍后，相信大家都对什么是二叉搜索树有了较为清晰的认识。接下来说一下二叉搜索树的一些基本操作。

二、二叉搜索树的基本操作

二叉树的结构

typedef int ElementType;
typedef struct TNode *Position;
typedef Position BinTree; /* 二叉树类型 */
struct TNode{ /* 树结点定义 */ElementType Data; /* 结点数据 */BinTree Left;     /* 指向左子树 */BinTree Right;    /* 指向右子树 */
};

1. 二叉搜索树的查找操作：

（1）查找从根结点开始，如果树为空，返回NULL
（2）若搜索树非空，则根结点关键字和X进行比较，并进行不同处理：
① 若X小于根结点键值，只需在左子树中继续搜索；
② 如果X大于根结点的键值，在右子树中进行继续搜索；
③若两者比较结果是相等，搜索完成，返回指向此结点的指针。

下图为在这棵树中寻找X的示意图：如果X大于r，就继续去T_R找；如果X小于r，就去T_L找，如果相等，那么查找成功，直接返回。

在这里插入图片描述
代码如下：

Position Find( ElementType X, BinTree BST )
{if( !BST ) return NULL; /*查找失败*/if( X > BST->Data )return Find( X, BST->Right ); /*在右子树中继续查找*/else if( X < BST->Data )return Find( X, BST->Left ); /*在左子树中继续查找*/else /* X == BST->Data */return BST; /*查找成功，返回结点的找到结点的地址*/
}

值得说明的是，上述的代码使用的是递归的方式，而使用递归会导致效率不高。恰巧这段代码又是尾递归的方式（尾递归就是程序分支的最后，也就是最后要返回的时候才出现递归），从编译的角度来讲，尾递归都可以用循环的方式去实现。由于非递归函数的执行效率高，可将“尾递归”函数改为迭代函数。

代码如下：

Position IterFind( ElementType X, BinTree BST )
{while( BST ) {if( X > BST->Data )BST = BST->Right; /*向右子树中移动，继续查找*/else if( X < BST->Data )BST = BST->Left; /*向左子树中移动，继续查找*/else /* X == BST->Data */return BST; /*查找成功，返回结点的找到结点的地址*/}return NULL; /*查找失败*/
}

最后要说的是，查找的效率决定于树的高度。

2. 查找最大和最小元素
首先说明的是：
①最大元素一定是在树的最右分枝的端结点上。
②最小元素一定是在树的最左分枝的端结点上。
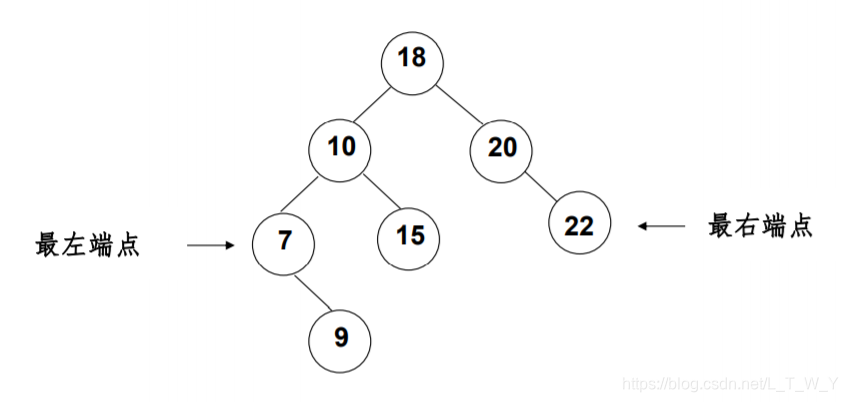
在这里插入图片描述

根据上述两点，我们可以很轻松的把代码写出来：

Position FindMin( BinTree BST )
{if( !BST ) return NULL; /*空的二叉搜索树，返回NULL*/else if( !BST->Left )return BST; /*找到最左叶结点并返回*/elsereturn FindMin( BST->Left ); /*沿左分支继续查找*/
}

上面是查找最小元素的递归函数，由于这也是个尾递归，所以我们依旧可以把它改成迭代函数，在这里我就不重复写了，直接写查找最大元素的迭代函数。代码如下：

Position FindMax( BinTree BST )
{if(BST )while( BST->Right )  /*沿右分支继续查找，直到最右叶结点*/BST = BST->Right;return BST;
}

3. 二叉搜索树的插入
二叉搜索树在插入前，肯定要找到插入的位置。所以解决这个问题的关键就是要找到元素应该插入的位置，可以采用与Find类似的方法。下图演示了在二叉搜索树中插入35的过程。
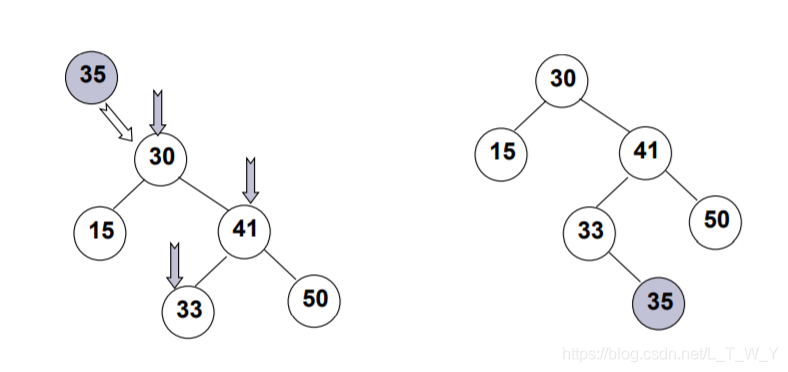
在这里插入图片描述
代码如下：

BinTree Insert( BinTree BST, ElementType X )
{if( !BST ){ /* 若原树为空，生成并返回一个结点的二叉搜索树 */BST = (BinTree)malloc(sizeof(struct TNode));BST->Data = X;BST->Left = BST->Right = NULL;}else { /* 开始找要插入元素的位置 */if( X < BST->Data )BST->Left = Insert( BST->Left, X );   /*递归插入左子树*/else  if( X > BST->Data )BST->Right = Insert( BST->Right, X ); /*递归插入右子树*//* else X已经存在，什么都不做 */}return BST;
}

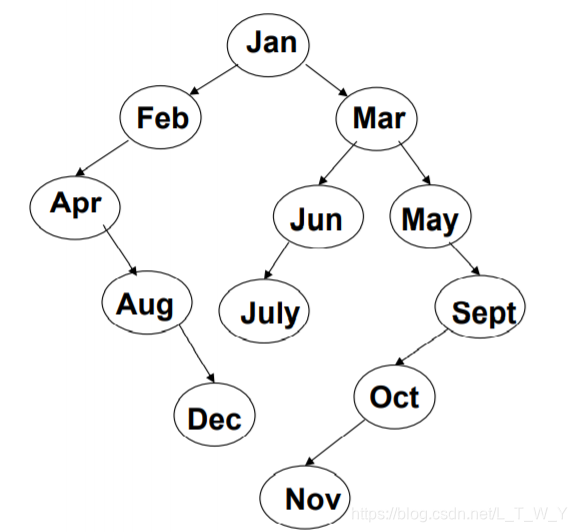
举个例子：以一年十二个月的英文缩写为键值，按从一月到十二月顺序输入，即输入序列为（Jan, Feb, Mar, Apr, May, Jun, July, Aug, Sep,Oct, Nov, Dec）。想一想结果是怎么样的呢？如下图所示：
在这里插入图片描述

4. 二叉搜索树的删除
对于二叉搜索树的删除，相对来说就比较麻烦了。因为要考虑以下三种情况：
①要删除的是叶结点；
②要删除的结点只有一个孩子结点；
③要删除的结点有左、右两棵子树；

对于上述的三种情况，我们要怎么做呢？

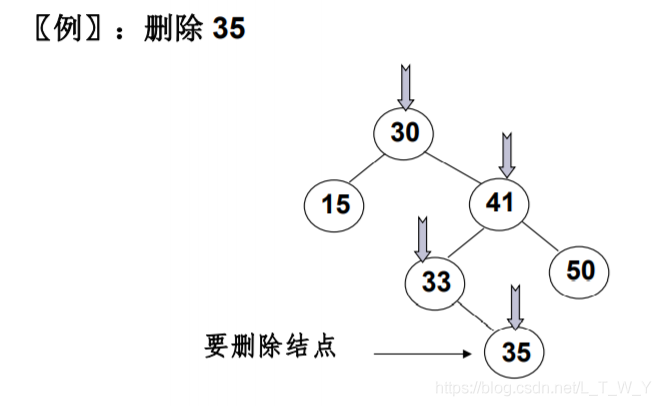
情况①：
叶结点就是左右子树都为空的结点，既然左右子树都为空，删掉它并没什么后顾之忧，所以当我们要删除的是叶结点的时候，直接删除就好了。当然不要忘记一个重要的操作——删除之后要修改其父结点指针，即置为NULL。

举个例子方便理解：如下图所示：
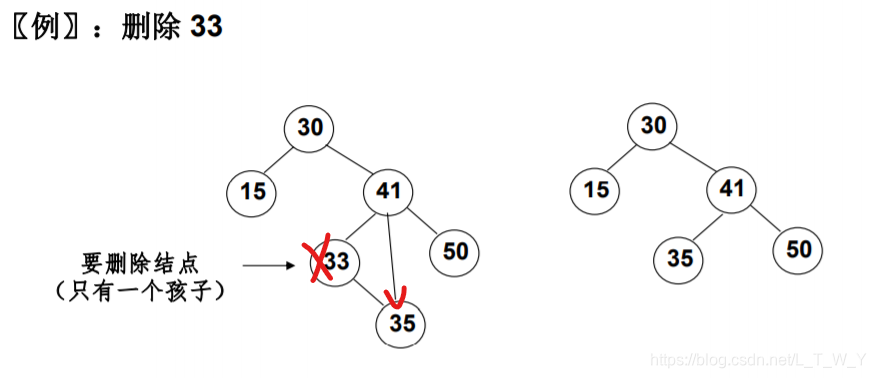
在这里插入图片描述
情况②：
当要删除的结点只有一个孩子结点，我们删除该结点后需要考虑怎么处置它的孩子结点。因为被删除的结点的孩子无论是左孩子还是右孩子，都只会比被删除的结点的父结点小，所以我们只需要将被删除的结点的父结点的指针指向被删除的结点的孩子结点。

举个例子方便理解：如下图所示：
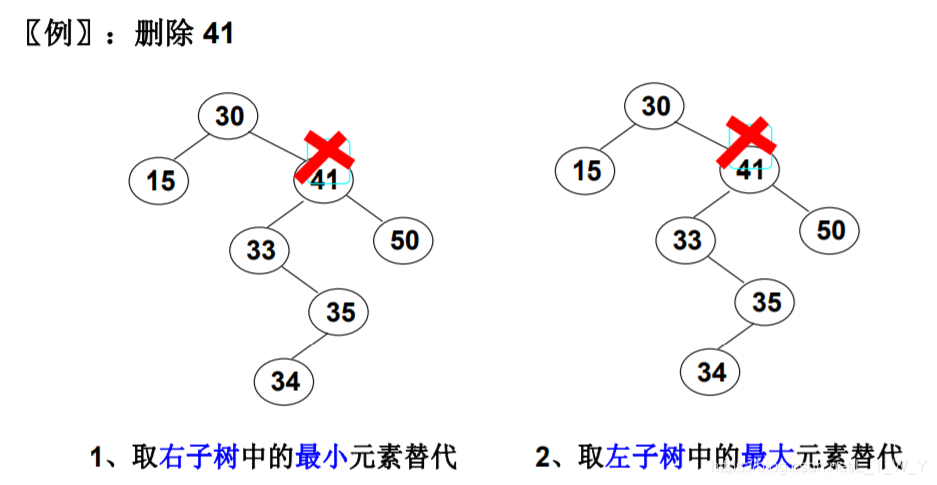
在这里插入图片描述 情况③：
当删除的结点有左、右两棵子树，我们删除该结点后需要考虑怎么处置它的孩子结点。此时最简单的办法就是用另一结点替代被删除结点，那我们要用哪一个结点呢？根据二叉搜索树的定义：每一个结点的右孩子都比自己大，左孩子都比自己小。要取哪一个结点替代被删除的结点同时又保证该特性呢？所以根据此情况，我们很快就能判断出用被删除结点的右子树的最小元素或者左子树的最大元素替代被删除结点。

举个例子方便理解：如下图所示：
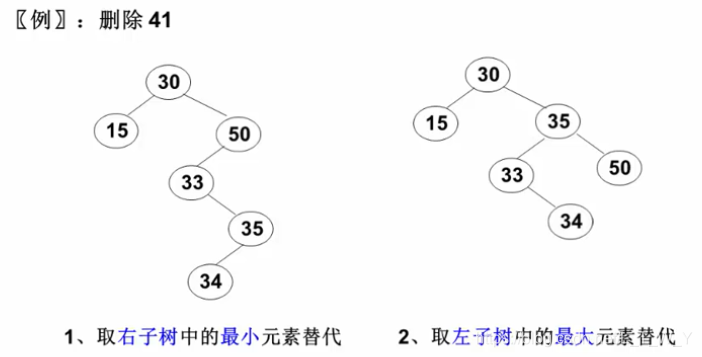
在这里插入图片描述

在这里插入图片描述
值得注意的是：当我们找到元素替代被删除的结点后，我们也要删除用来替代元素。删除该元素的方法也是按照以上3种情况分析

上述三种情况分析完之后，就要用代码把他们表示出来了，代码如下：

BinTree Delete( BinTree BST, ElementType X ) 
{ Position Tmp; if( !BST ) printf("要删除的元素未找到"); else {if( X < BST->Data ) BST->Left = Delete( BST->Left, X );   /* 从左子树递归删除 */else if( X > BST->Data ) BST->Right = Delete( BST->Right, X ); /* 从右子树递归删除 */else { /* BST就是要删除的结点 *//* 如果被删除结点有左右两个子结点 */ if( BST->Left && BST->Right ) {/* 从右子树中找最小的元素填充删除结点 */Tmp = FindMin( BST->Right );BST->Data = Tmp->Data;/* 从右子树中删除最小元素 */BST->Right = Delete( BST->Right, BST->Data );}else { /* 被删除结点有一个或无子结点 */Tmp = BST; if( !BST->Left )       /* 只有右孩子或无子结点 */BST = BST->Right; else                   /* 只有左孩子 */BST = BST->Left;free( Tmp );}}}return BST;
}