1. 二叉搜索树的应用

(1)K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。

比如：车牌门禁系统，把一个小区的车牌号数据录入二叉搜索树，此时Key类型为string，string是支持比较大小的。如果在搜索树中存在此车牌号就放行，如果不存在就报警告。

再比如检查一篇文章单词释放拼写错误：以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树，在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。(比如typora、VS的拼写检查等)。

**(2) KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。**该种方式在现实生活中非常常见：

比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对

再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出现次数就是<word, count>就构成一种键值对。

2. 二叉搜索树的KV模型

我们把前面Key模型的二叉搜索树改造为KV模型。

首先，我们的目的是查找Key的时候随便查找Value，所以节点的结构、Insert和new的时候都要增加第二个参数Value。其次FindR要返回节点的指针，因为不允许修改Key，但可以修改Value。查找和删除不需要是因为都是基于Key来查找或者删除。

namespace key_value
{
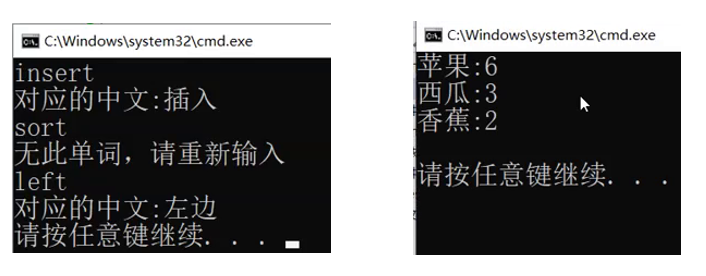
#pragma oncetemplate<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;const K _key;// 防止修改Key破坏结构V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:void InOrder(){_InOrder(_root);cout << endl;}///Node* FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key, const V& value){return _InsertR(_root, key, value);}bool EraseR(const K& key){return _EraseR(_root, key);}private:bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;// 删除if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}swap(root->_key, minRight->_key);return _EraseR(root->_right, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key, const V& value){if (root == nullptr){root = new Node(key, value);return true;}if (root->_key < key)return _InsertR(root->_right, key, value);else if (root->_key > key)return _InsertR(root->_left, key, value);elsereturn false;}Node* _FindR(Node* root, const K& key){if (root == nullptr)return nullptr;if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return root;}}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};void TestBSTree1(){BSTree<string, string> ECDict;ECDict.InsertR("root", "根");ECDict.InsertR("string", "字符串");ECDict.InsertR("left", "左边");ECDict.InsertR("insert", "插入");//...string str;while (cin >> str)  //while (scanf() != EOF){//BSTreeNode<string, string>* ret = ECDict.FindR(str);auto ret = ECDict.FindR(str);if (ret != nullptr){cout << "对应的中文:" << ret->_value << endl;//ret->_key = "";ret->_value = "";}else{cout << "无此单词，请重新输入" << endl;}}}void TestBSTree2(){string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };// 水果出现的次数BSTree<string, int> countTree;for (const auto& str : arr){auto ret = countTree.FindR(str);if (ret == nullptr){countTree.InsertR(str, 1);}else{ret->_value++;  // 修改value}}countTree.InOrder();}
}

测试结果：

3. 关于const K导致无法erase

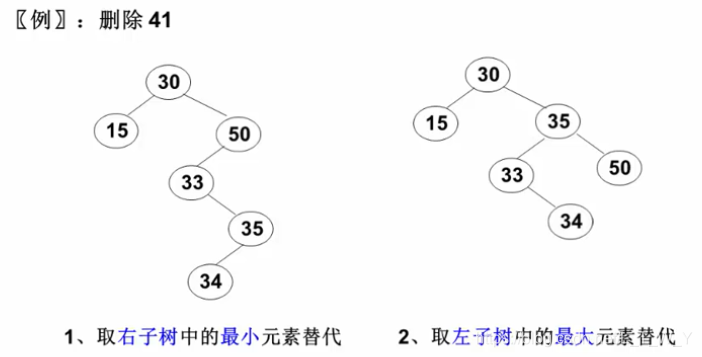
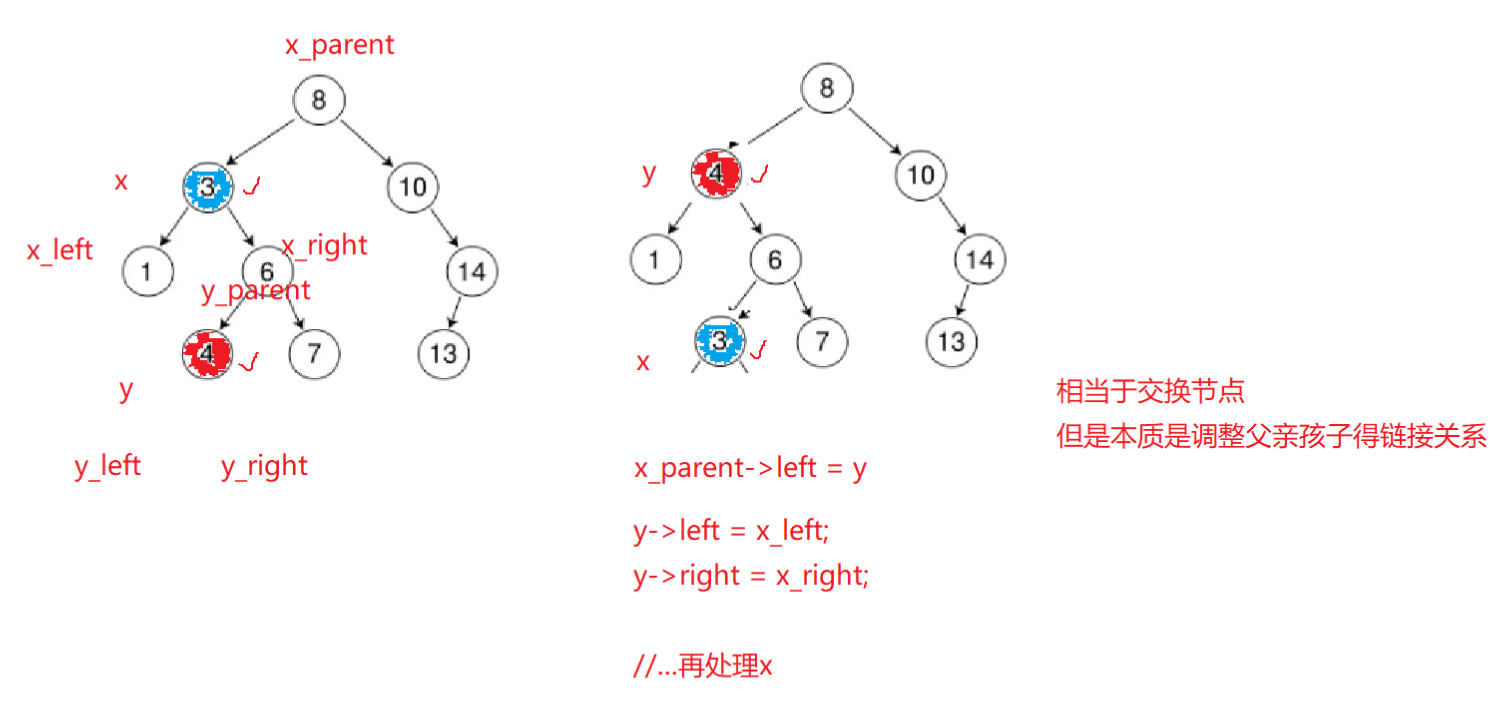
因为K无法修改，导致删除节点时，如果这个节点左右孩子都不为空，用替换法删除时无法交换两个节点的值。这个时候就得把两个节点做真正意义上的交换，但是本质是调整两个节点的父子节点的链接关系。

4. 关于while (cin >> str)

**类型可以重载。**通过重载强制类型转换符号(C++重载())，没有返回值，是C++的特殊处理。

cin对象不能用做条件判断的值，实际上cin可以转换为void*或者bool类型，做条件判断时实际上不是真的转换了，而是去调用函数来转换。

为了防止自定义类型转换成bool类型或者其他类型，在重载类型时加上explicit关键字。

class A
{
public:explicit A(int a = 0):_a(a){}//operator bool()//{//	if (_a < 10)//	{//		return true;//	}//	else//	{//		return false;//	}//}explicit operator int(){if (_a < 10){return 1;}else{return 0;}}void Print(){cout << _a << endl;}void Set(int a){_a = a;}private:int _a;
};void test()
{//list<int>::iterator it;//*it; --> it.operator*()//A aa = 10;A a;//bool ret = a;//int y = a;int x;//while (a.operator bool())while (a){a.Print();cin >> x;a.Set(x);}
}

5. 面试oj题

5.1根据二叉树创建字符串

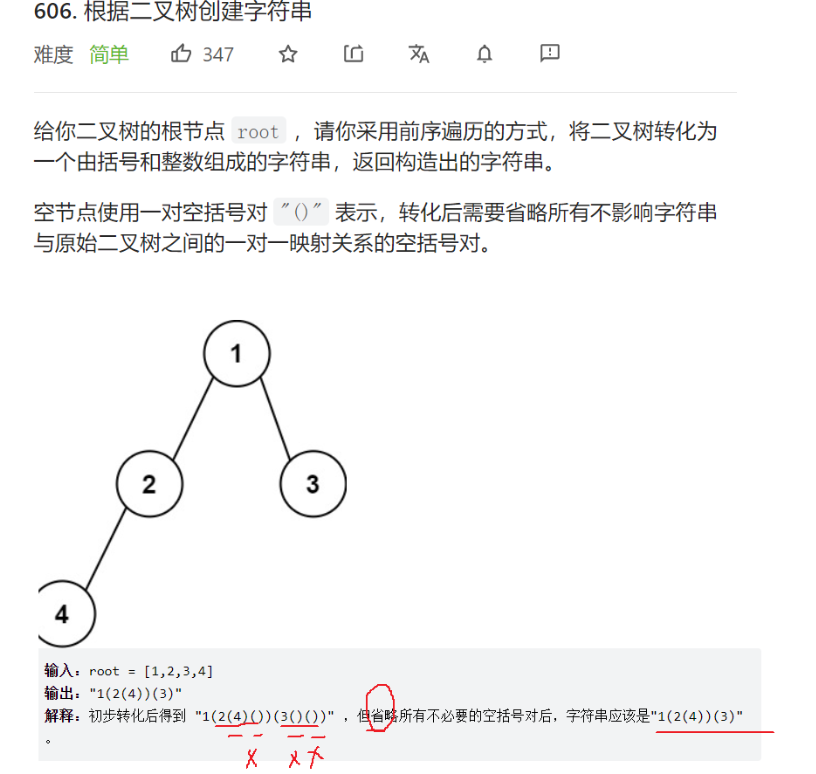
606. 根据二叉树创建字符串

因为是前序创建字符串，所以左子树为空，右子树不为空以及左右子树都为空是不必要的空括号对。

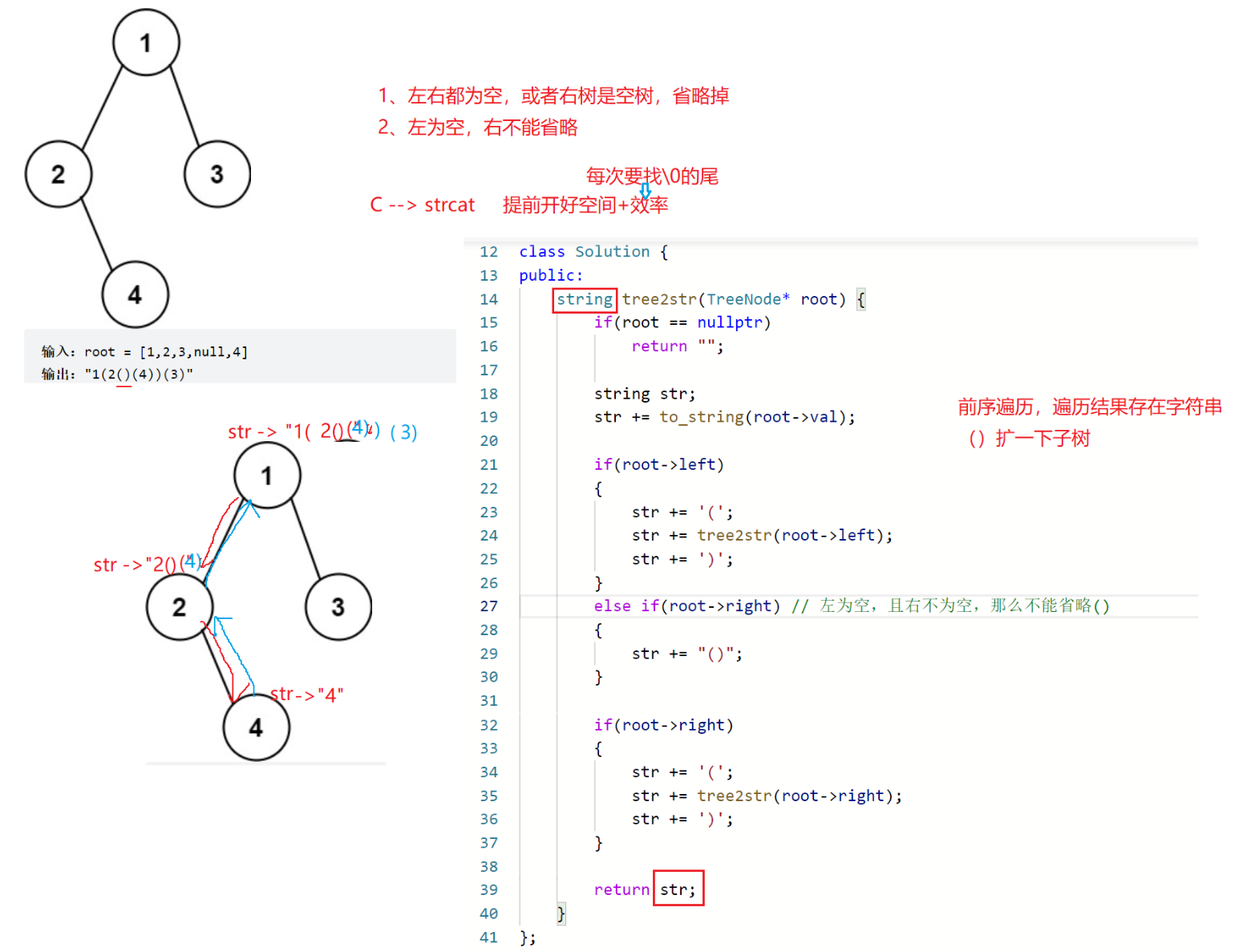
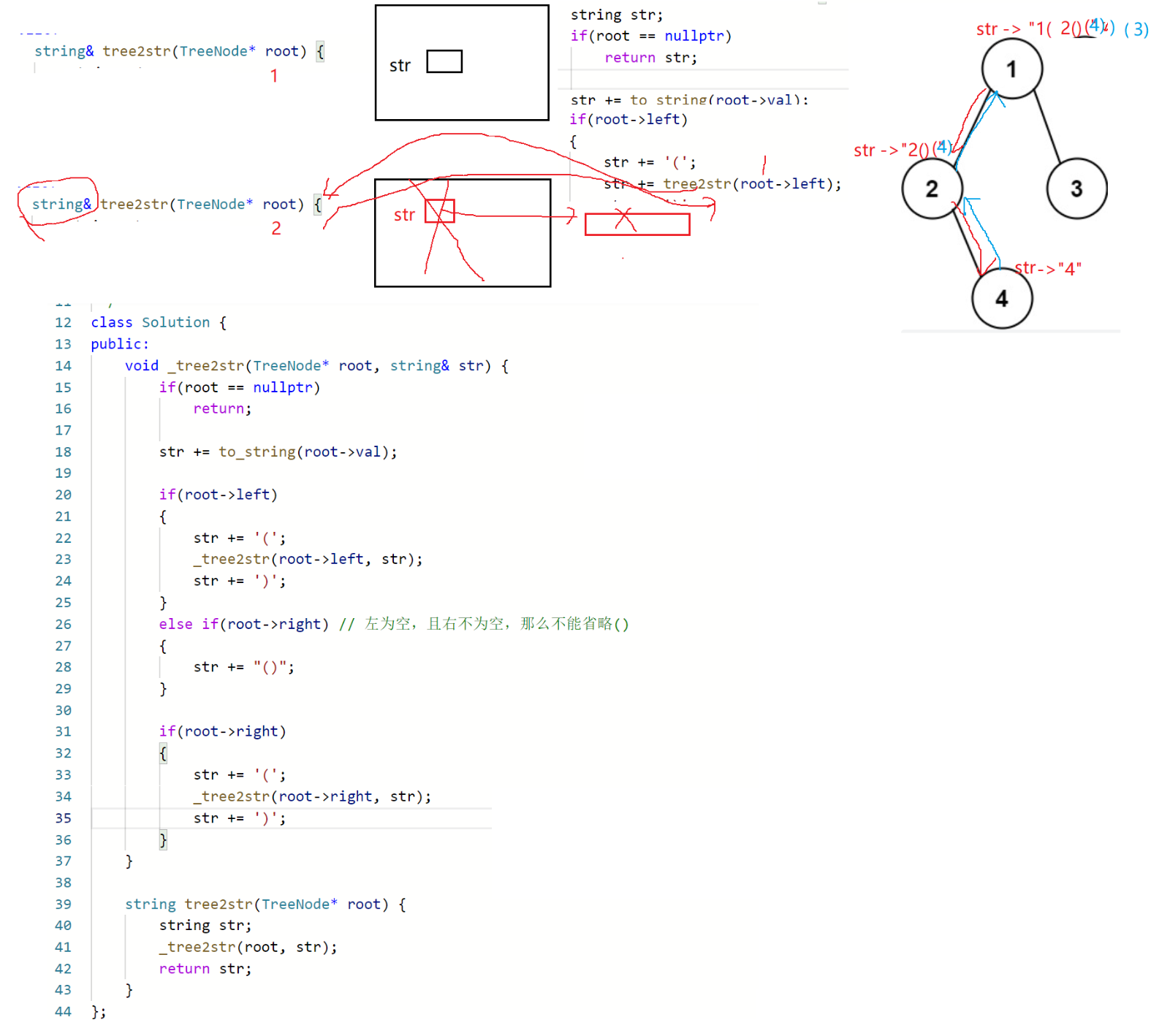
但是传值返回会不断创建临时变量调用构造函数，为了优化我们可以再套一层，使得全程只有一个str对象。

不能用引用返回的原因是递归返回时会销毁局部变量。

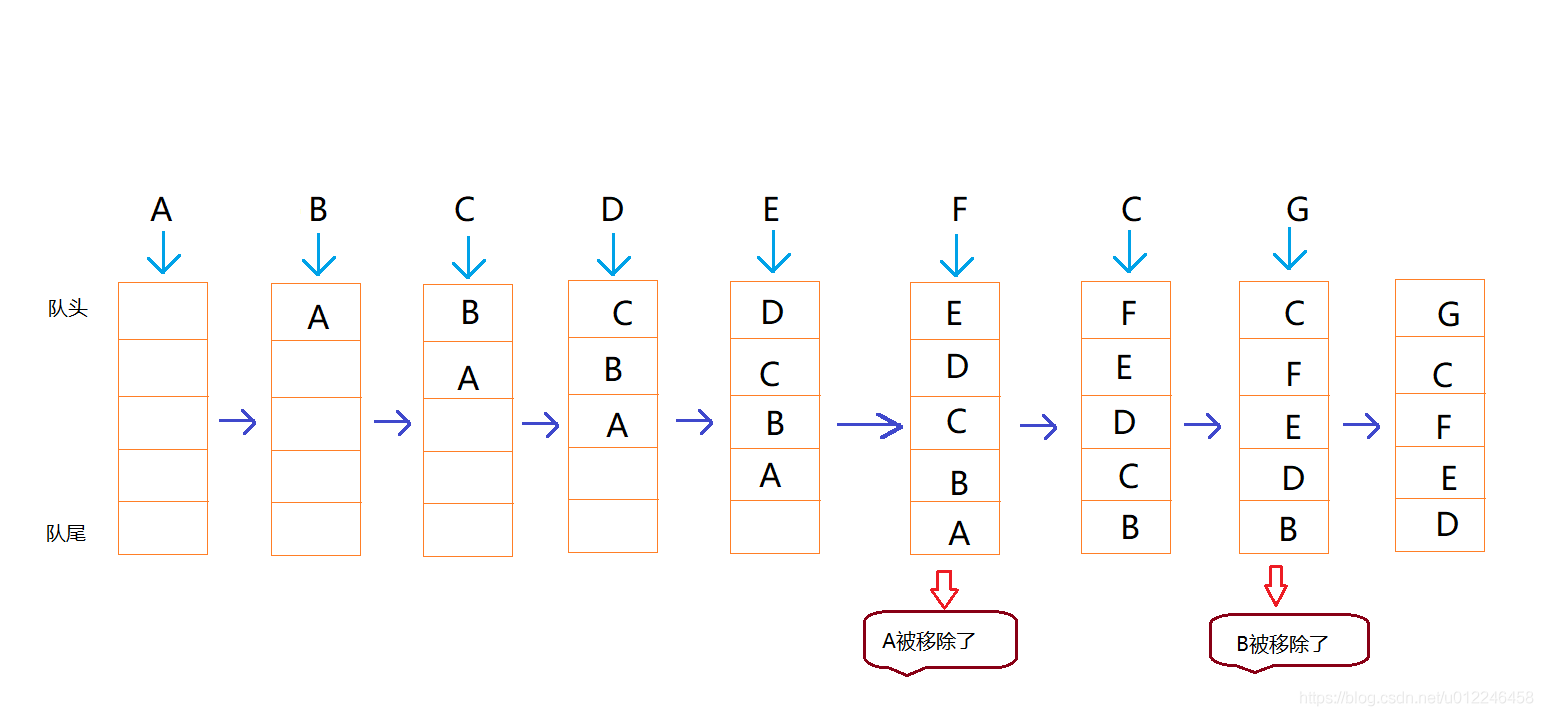
5.2二叉树的层序遍历

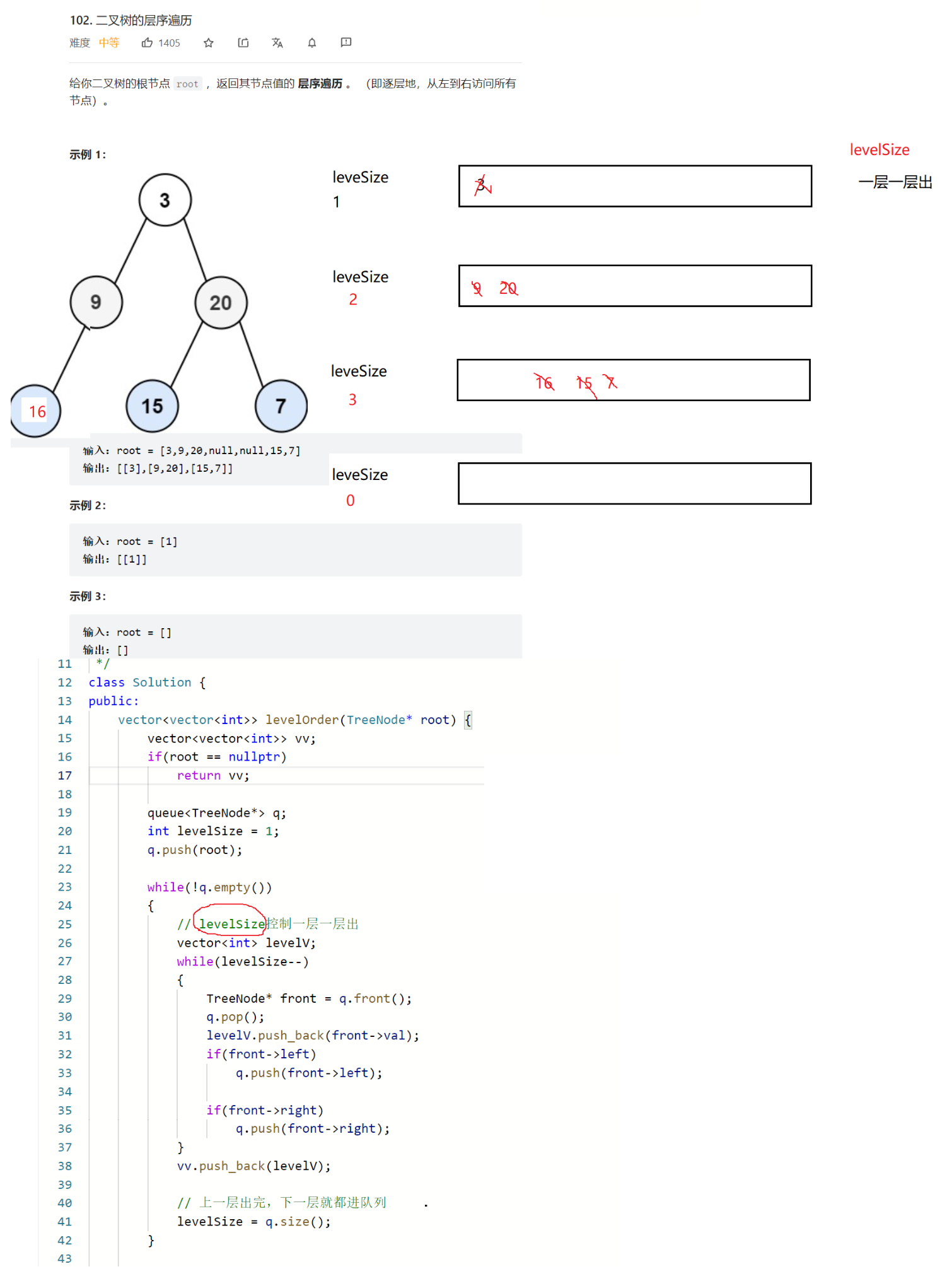
102. 二叉树的层序遍历

利用levelSize控制一层一层出队列。

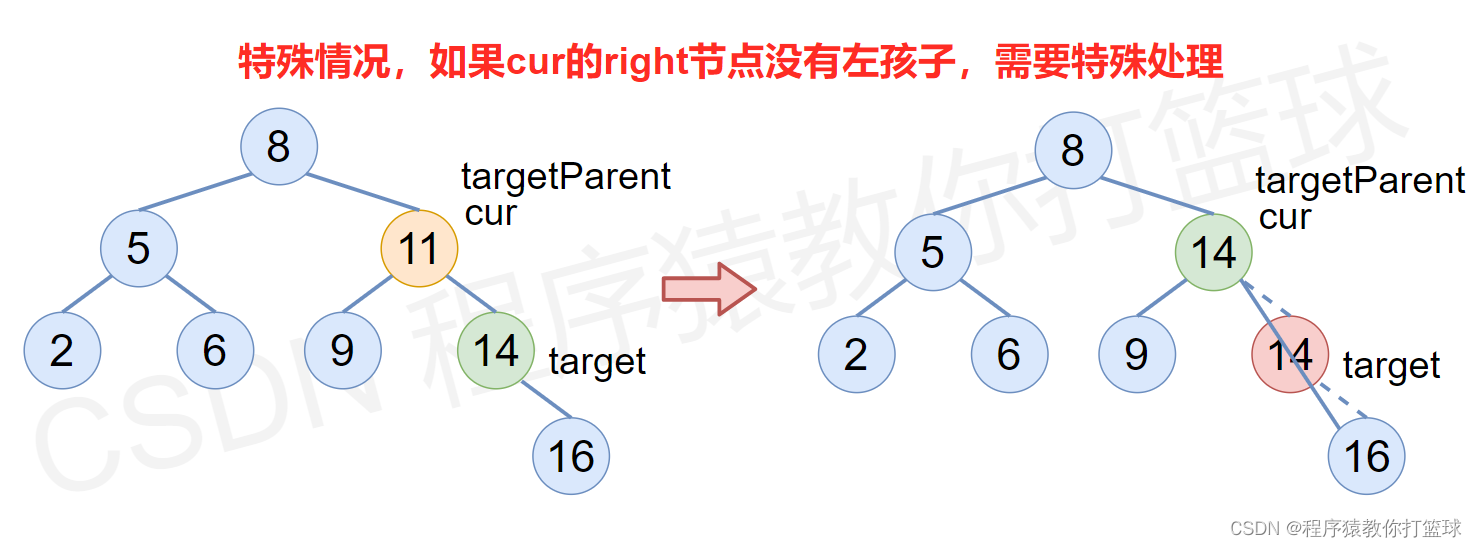
5.3二叉树的最近公共祖先

236. 二叉树的最近公共祖先

结论:如果p、q分别在一个节点的左右两边，那么该节点就是最近公共祖先，如果都在该节点的左边或者右边就不是公共祖先，继续递归去找公共祖先。

下图第四种情况是特例。

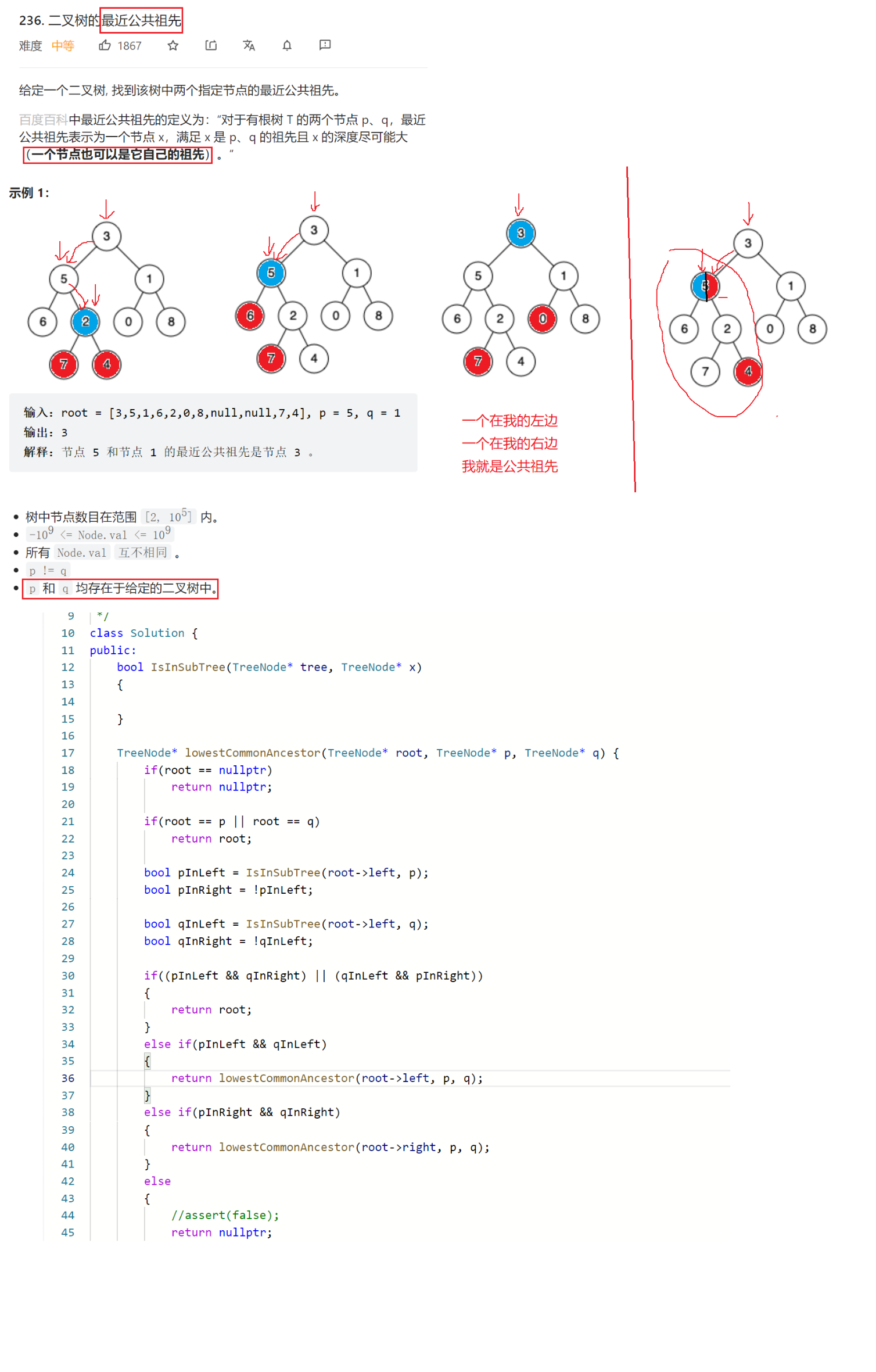
bool IsInSubTree(TreeNode* tree, TreeNode* x)
{if(tree == nullptr)return false;if(tree == x)return true;return IsInSubTree(tree->left,x)|| IsInSubTree(tree->left,x);
}

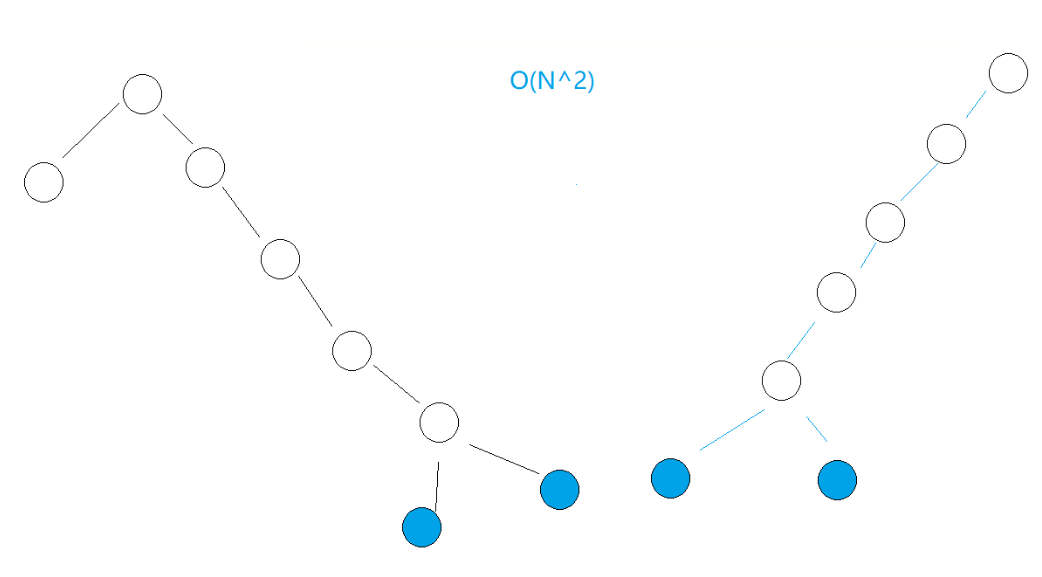
但是这种解法在极端场景下时间复杂度是O(n^2)，比如下图，此时p、q递归时每次都要把root的后辈节点找一遍，等差数列。

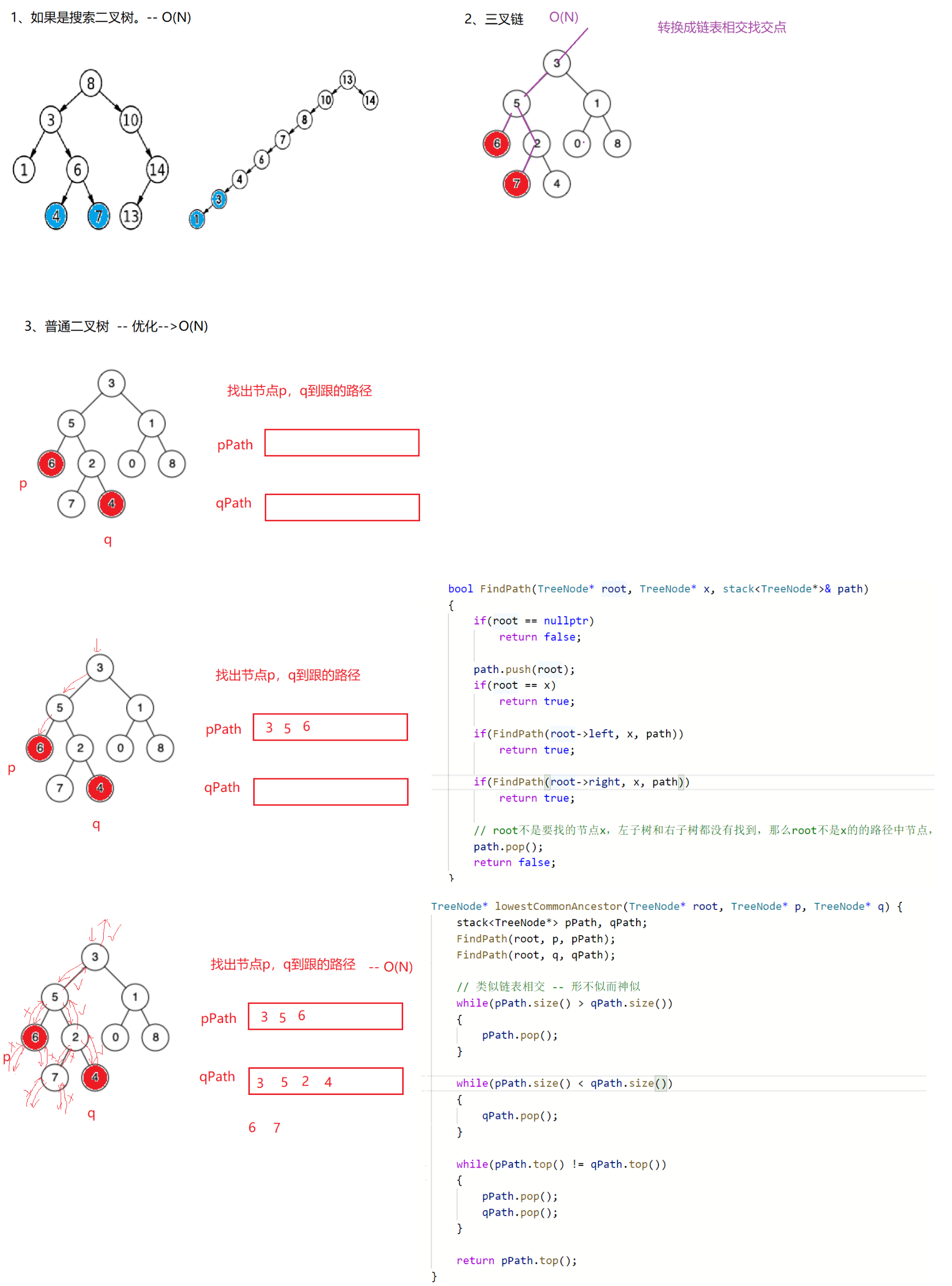
考虑用栈来存储p、q的路径，让路径长的先走，路径相等后同时走，转换成求两个路径的交点。

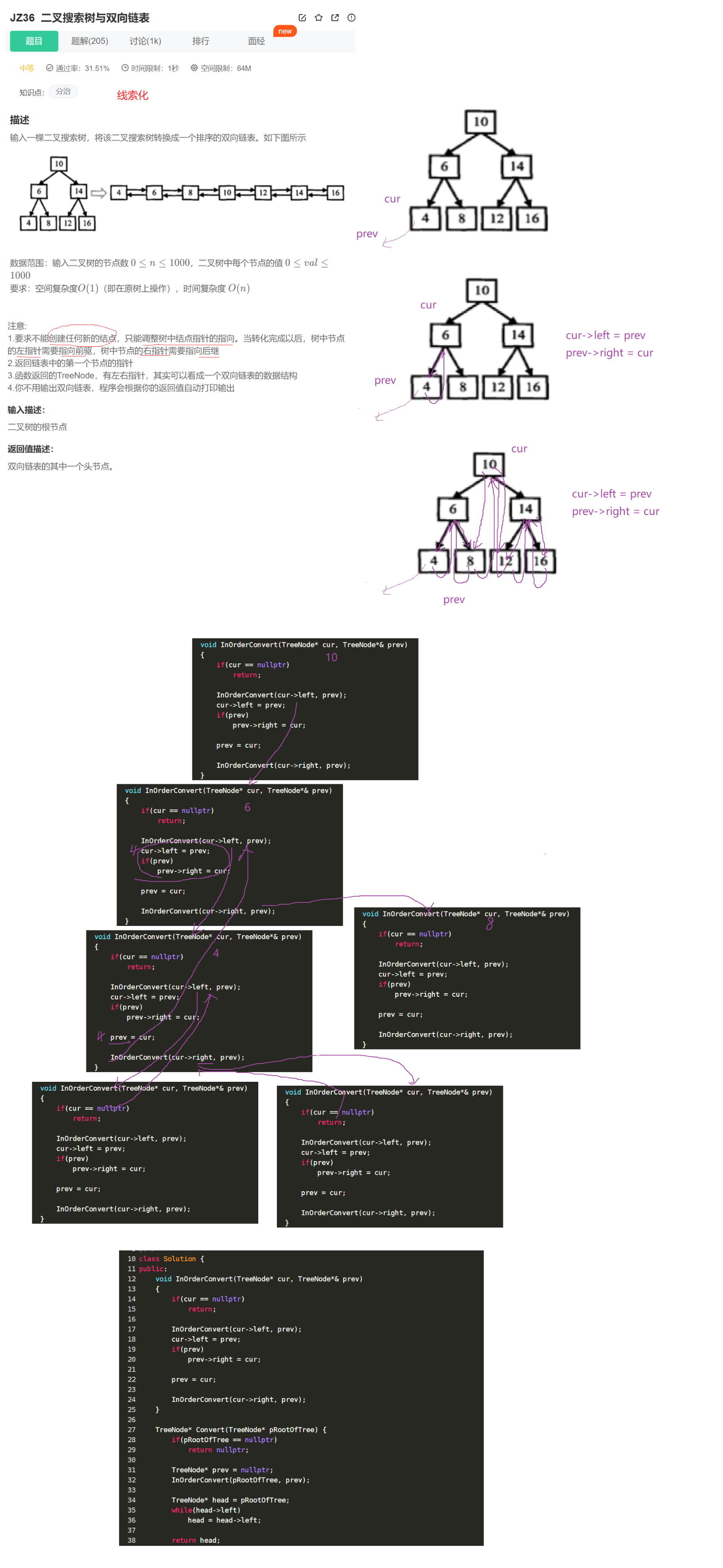
5.4 二叉搜索树与双向链表

二叉搜索树与双向链表

递归时，我们很容易知道当前节点的前一个节点是什么，但是无法知道下一个节点是什么，所以我们不能改变当前节点的右指针(后继指针)。因此我们让当前节点的左指针(前驱指针)指向中序遍历的前一个，让前一个的右指针(后继指针)指向当前节点。

5.5从前序与中序遍历序列构造二叉树

105. 从前序与中序遍历序列构造二叉树

5.6二叉树的前序遍历迭代版

144. 二叉树的前序遍历迭代版

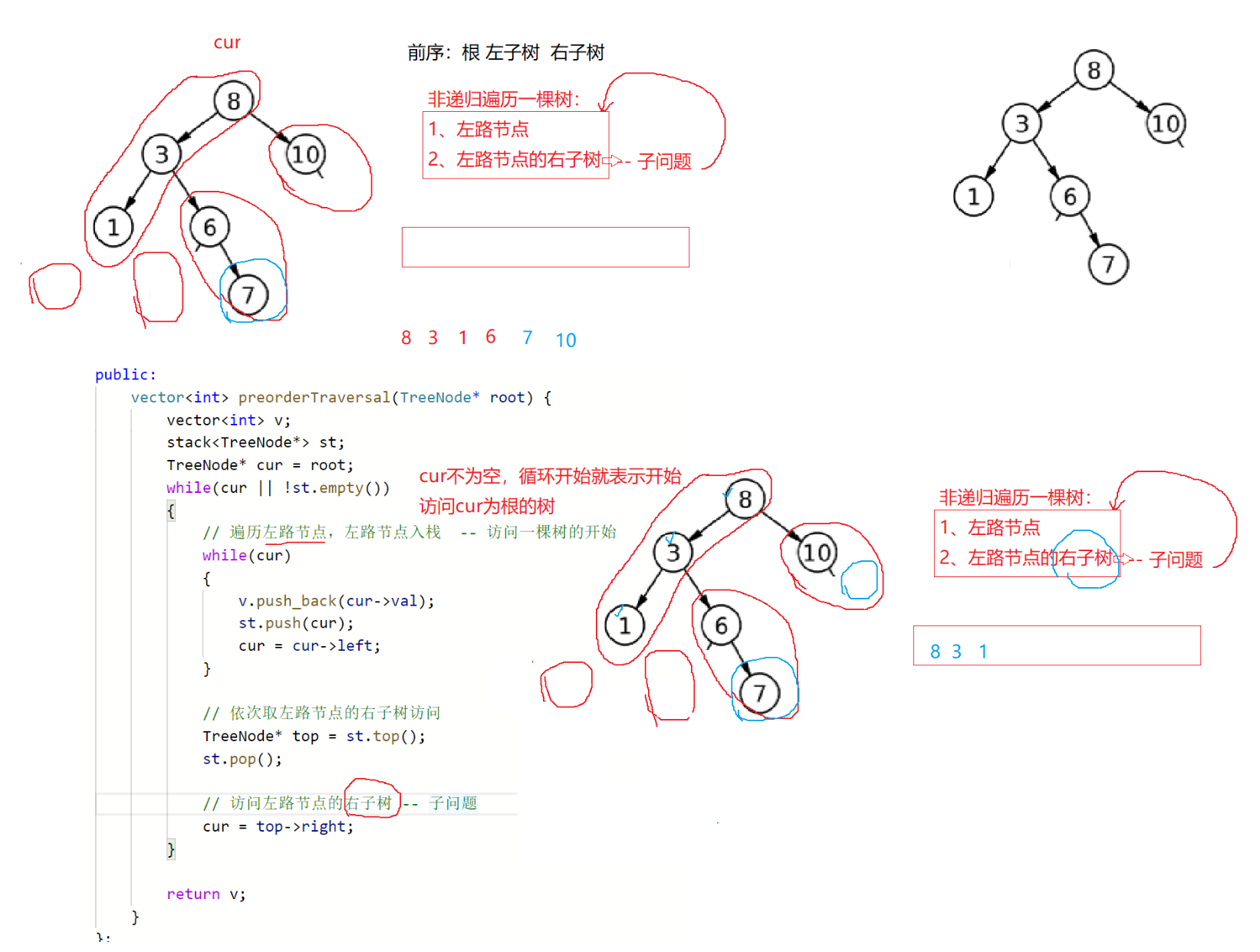
5.7二叉树的中序遍历迭代版

94. 二叉树的中序遍历迭代版

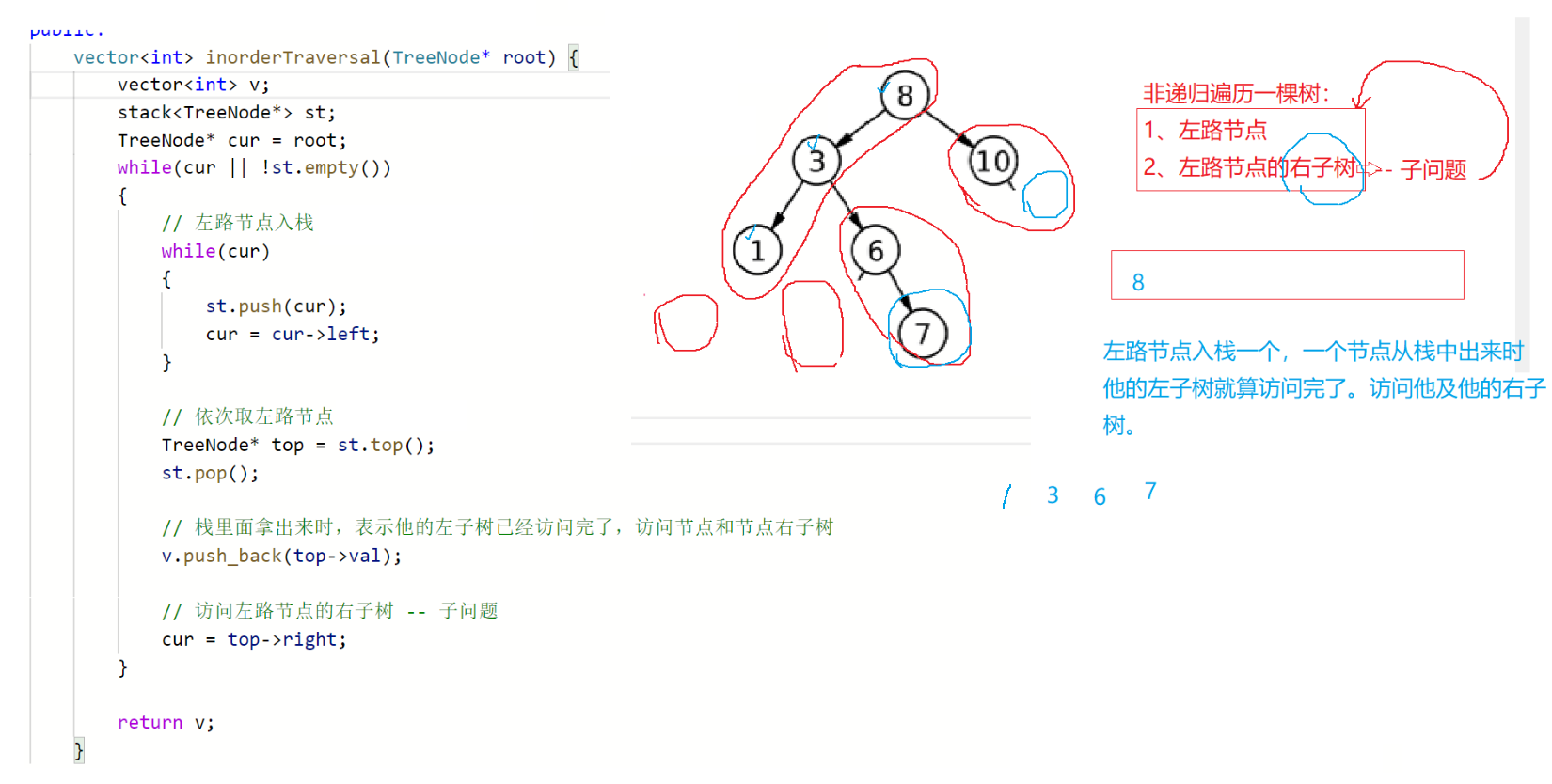
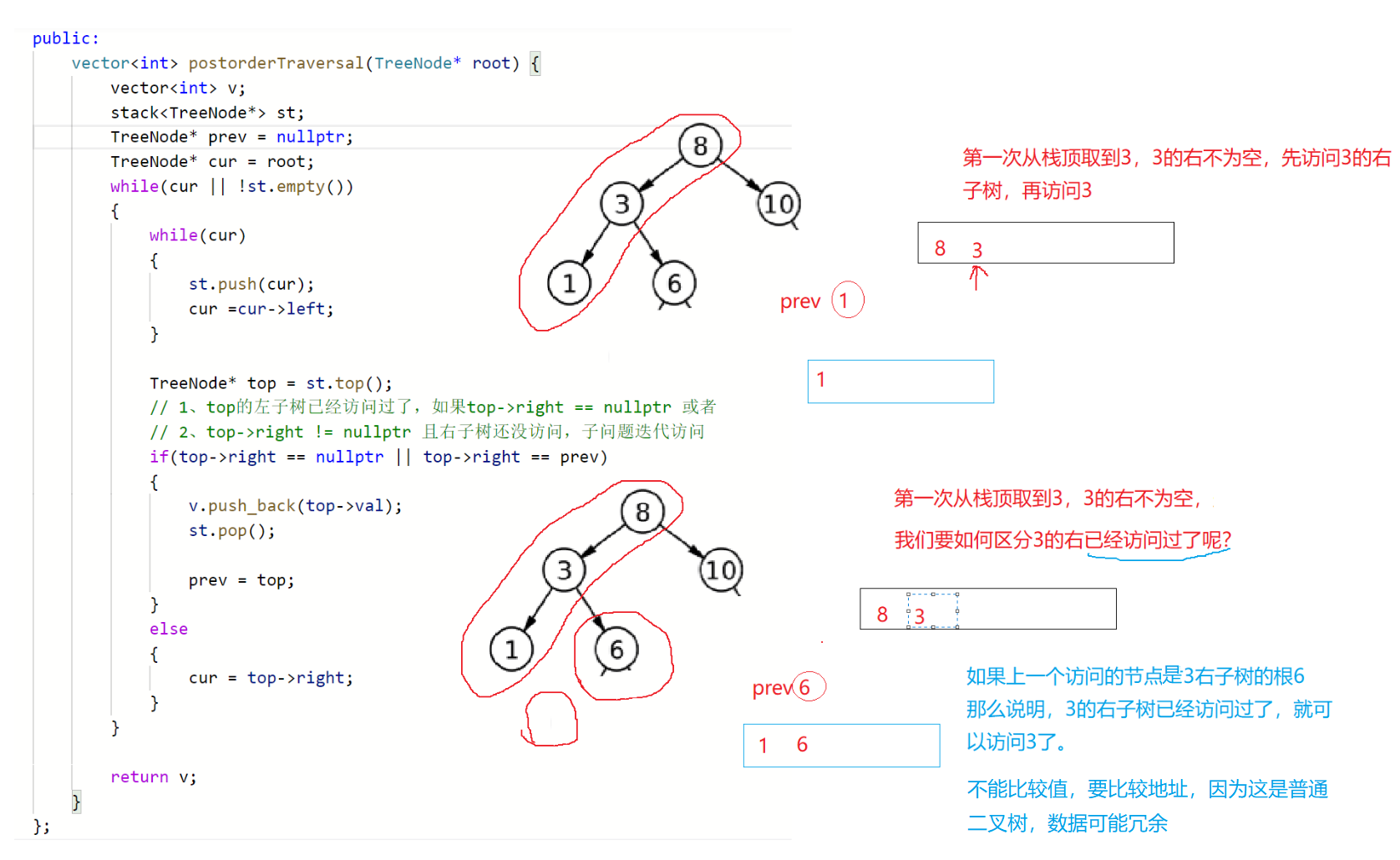
5.8 二叉树的后序遍历迭代版

145. 二叉树的后序遍历迭代版