一、概念

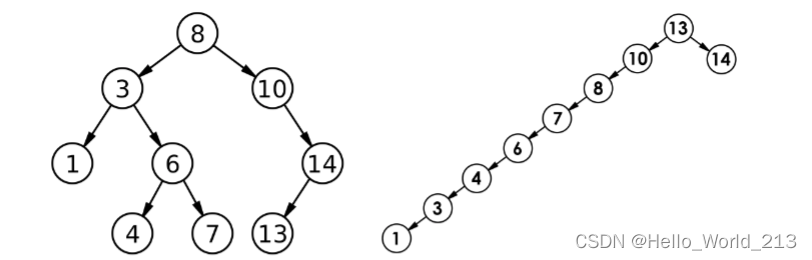
二叉搜索树又称二叉排序树
它或者是一棵空树，或者是具有以下性质的二叉树:
1.若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
2.若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
3.它的左右子树也分别为二叉搜索树
ps:二叉搜索树的中序遍历一定是有序的（从小到大）
在这里插入图片描述
（图片来自比特就业课）

二、相关操作

2.0节点相关代码：

class Node{//和二叉树没有什么区别public int val;public Node left;public Node right;public Node(int val){this.val=val;}
}

2.1查找

在这里插入图片描述
（图片来自比特就业课）

代码如下（示例）：

public Node search(int key){Node cur=root;while(cur!=null){if(cur.val<key){cur=cur.right;}else if(cur.val==key){return cur;}else{cur=cur.left;}}return null;//走到这里，说明上面while没找到，也就是没有这个数据}

2.2插入

二叉搜索树的插入分两种情况：
1.树本身就空的，你直接插入即可

2.树不是空树，但由于二叉搜索树的有序性质，如下图，我们要插入1给元素10的节点，10比5大，往右走；10比7大，往右走；10比8大，往右走；10比9大，往右走；发现9右边没有节点了，10就放在9节点的右边。

ps:对于二叉搜索树这种特殊的树，插入的节点一定会在叶子节点
在这里插入图片描述
（图片来自比特就业课）
代码如下（示例）：

public boolean insert(int val){if(root==null){root=new Node(val);return true;}Node newNode=new Node(val);//要插入的节点Node cur=root;//用来遍历的节点Node parent=null;//这个节点是用来标记cur的位置的（方便知道最后插入节点parent左边还是右边）//你可以理解为，parent就是上一个cur位置while(cur!=null){if(cur.val< val){parent=cur;cur=cur.right;}else if(cur.val> val){parent=cur;cur=cur.left;}else{//两个数据相同（搜索二叉树中不存在相同数据的情况）return false;}}if(parent.val<val){parent.right=newNode;}else if(parent.val>val){parent.left=newNode;}return true;}

2.3删除（重难点）

删除分3种大情况，大情况下又分3种小情况:
我们这里设待删除结点为 cur, 待删除结点的双亲结点为 parent
1.cur.left == null
①cur 是 root，则 root = cur.right
如下图：我现在要删除5这个节点，5节点左边没有节点，把12变成root即可在这里插入图片描述

②cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
如下图p是11，cur是10，现在删除cur，那么让p的左孩子变成8即可
在这里插入图片描述

③cur 不是 root，cur 是 parent.right，则 parent.right = cur.right
如下图：要删除12，把要删除节点的父亲结点5与删除节点的右节点15连接
在这里插入图片描述

2.cur.right == null
①cur 是 root，则 root = cur.left
如下图，要删除19这个节点，19右边没有节点的，我们让12成为新的根即可
在这里插入图片描述

②cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
如下图：要删除12，把删除节点的双亲节点19与要删除节点的子节点8连接
在这里插入图片描述

③cur 不是 root，cur 是 parent.right，则 parent.right = cur.left
如下图：要删除30，把30的双亲节点19与30的左孩子节点连接
在这里插入图片描述

3.cur.left != null && cur.right != null
两种处理方法：
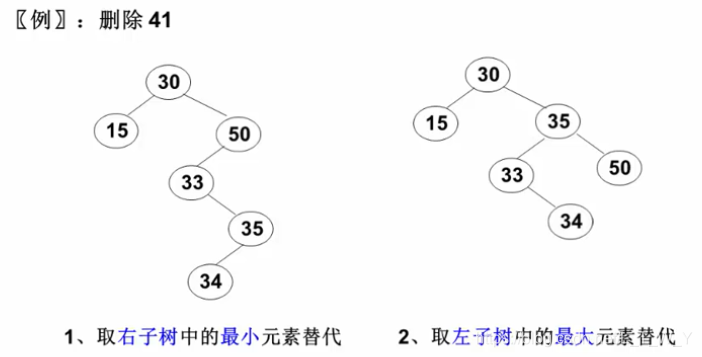
①在被删除节点的左子树找最大值，放被删除位置
②在被删除节点的右子树找最小值，放被删除位置
两种方法都是为了保证，删除掉某个节点后，该二叉树任然是二叉搜索树

如下图：我们现在要删70，怎么做？直接删吗？把90放在70的位置吗？假设把90放70的位置，那75是90的左节点啊，75怎么放呢？
在这里插入图片描述

这里先公布一下正确放法：

法一：把54放到70位置
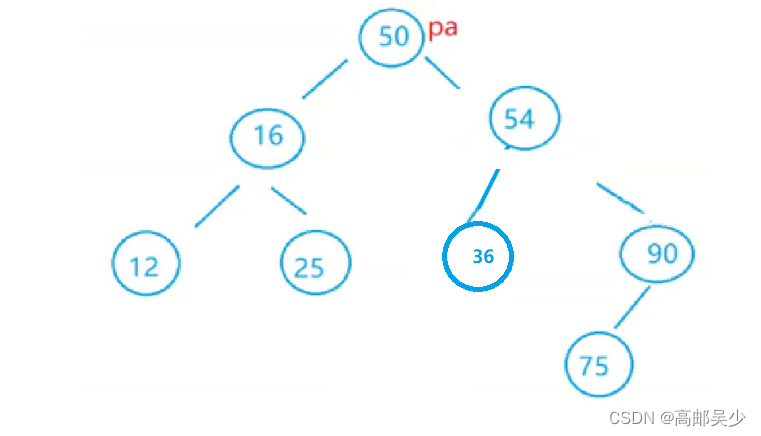
在这里插入图片描述

法二：把75放到70的位置，如下图
在这里插入图片描述
上面两种方法都可以保证删除掉某个节点后仍然是搜索二叉树

我们以法二进行举例，如何在要删除节点的右子树找最小值
在这里插入图片描述
遍历找到最小值75后，把75放到要删除数据70的位置，90与83连接，然后90与75,75与83的连接断开。
ps：这里90与83相连是83放90左边，但如果83是90以上的数，比如100，就要放在90的右边了，连接的时候需要进行判断一下。
（另一种方法类推即可，这里不过多赘述）
代码如下（示例）：

public void remove(int key){Node cur=root;Node parent=null;while(cur!=null){if(cur.val==key){//找到要删除的数了removeNode(cur,parent);//进行删除操作break;}else if(cur.val<key){parent=cur;cur=cur.right;}else{parent=cur;cur=cur.left;}}}public void removeNode(Node cur,Node parent){if(cur.left==null){//cur没有左孩子节点if(cur==root){root=cur.right;}else if(cur==parent.left){parent.left=cur.right;}else if(cur==parent.right){parent.right = cur.right;}}else if(cur.right==null){//cur没有右孩子节点if(cur==root){root=cur.left;}else if(cur==parent.left){parent.left=cur.left;}else if(cur==parent.right){parent.right=cur.left;}}else if(cur.left!=null&&cur.right!=null){//在要删除节点的右子树找最小值//我们这里创建变量，target表示要找的最小值节点Node targetParent=cur;//记录target的上一个位置Node target=cur.right;while(target.left!=null){//只往左边找（二叉搜索树左值<根<右值）targetParent=target;target=target.left;}cur.val=target.val;//target值放到要删除节点去if(target==targetParent.left){//target节点在它双亲节点左边，比如文章图中75在90左边targetParent.left=target.right;}else if(target==targetParent.right){targetParent.right = target.right;}}}

2.4测试用例

//用中序遍历（左根右），如果是二叉搜索树，则中序遍历一定是有序的public void inOrder(Node root){if(root==null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}public static void main(String[] args) {int []arr={10,8,19,3,9,4,7};BinarySearchTree binarySearchTree=new BinarySearchTree();//测试插入数据for(int i=0;i<arr.length;i++){binarySearchTree.insert(arr[i]);}binarySearchTree.inOrder(binarySearchTree.root);//打印3 4 7 8 9 10 19System.out.println();//测试插入重复数据boolean b=binarySearchTree.insert(7);System.out.println(b);//打印false//测试删除数据binarySearchTree.remove(8);binarySearchTree.inOrder(binarySearchTree.root);//打印3 4 7 9 10 19 （仍然有序，且没有8这个值）}