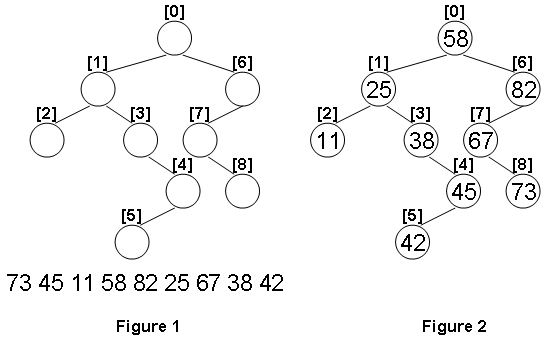
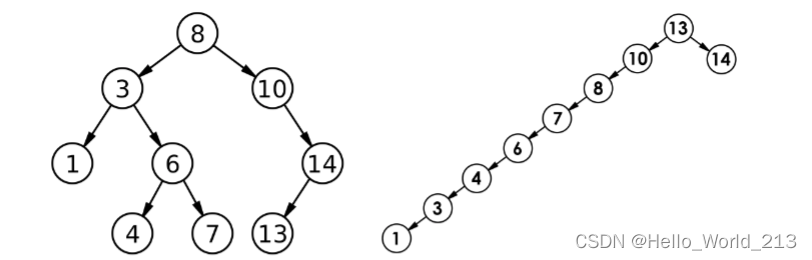
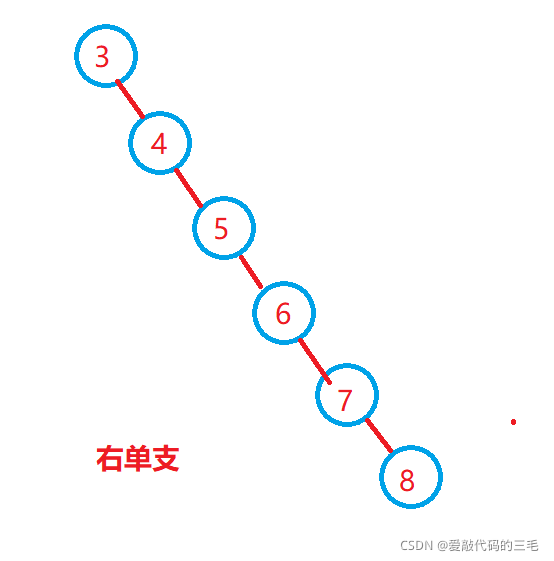
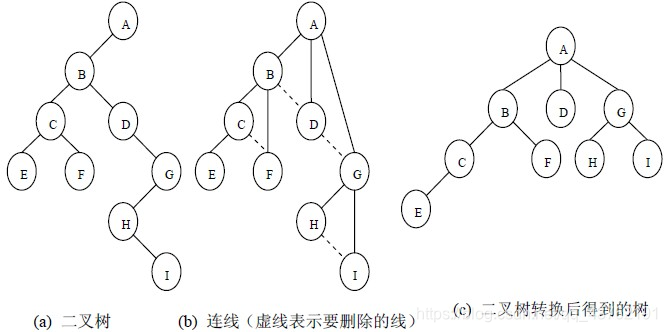
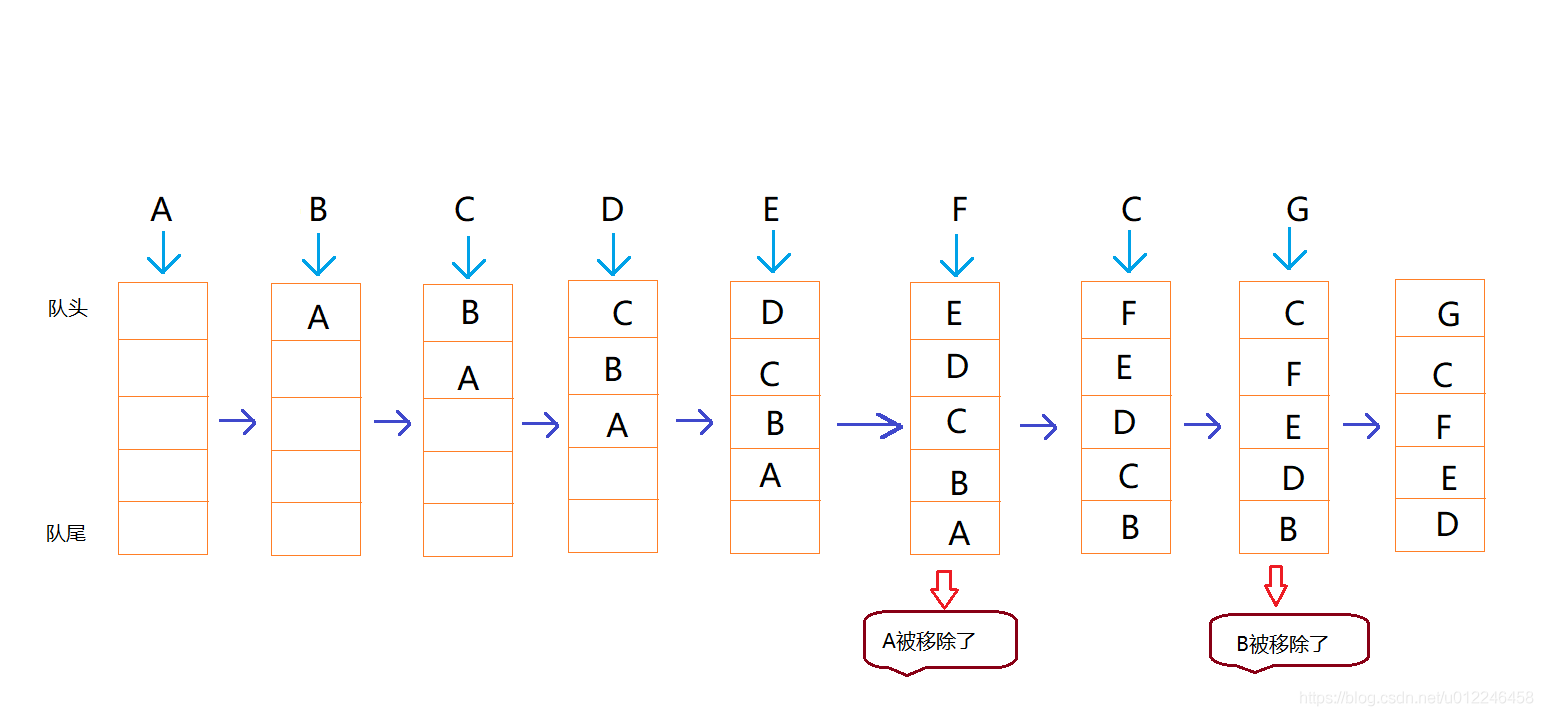
二叉搜索树(BST)，有时也被称为二叉排序树，是一种特殊类型的容器: 在内存中存储“项目”（例如数字，名称等）的数据结构。它们允许快速查找、添加和删除项目。二叉排序树是带根结点的二叉树，其内部结点各自存储一个关键字(以及可选的相关值),并且各自具有两个可区分的子树，通常表示为左和右。该树还拥有二分搜索的属性，该属性声明每个结点中的关键字必须大于或等于左子树中存储的任何关键字，并且小于或等于右子树中存储的任何关键字。 树的叶子(最终结点)不包含关键字，也没有结构来区分它们。 

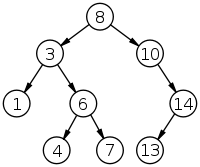
二叉搜索树结构如上图所示。下面将根据二叉搜索树的特点进行插入、查找和删除操作。 

##二叉搜索树
##本代码分别设计了二叉搜索树的插入、查找和删除操作
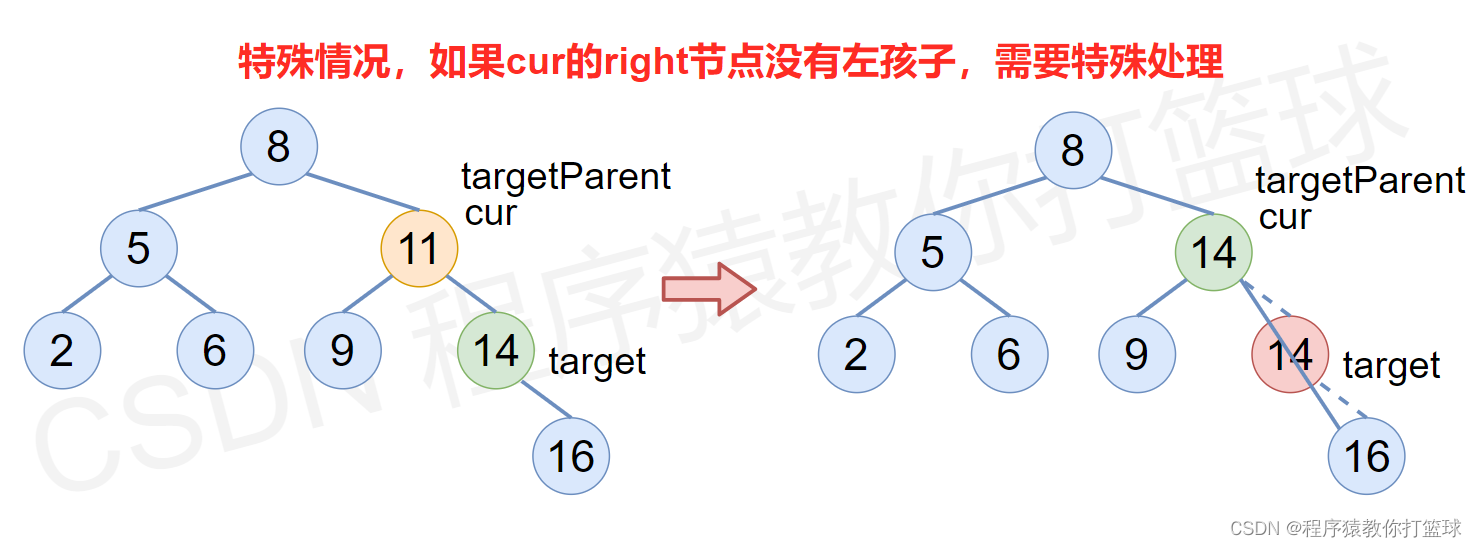
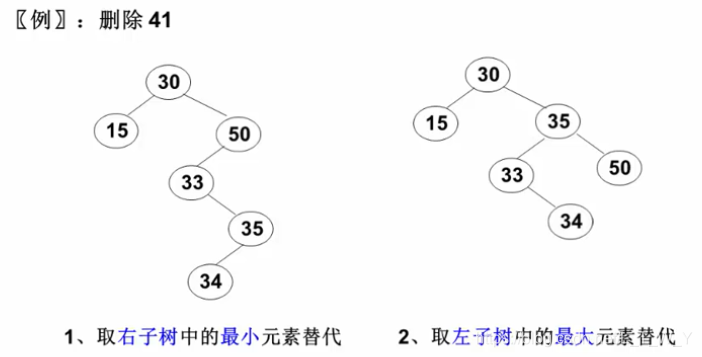
class ercha_tree():##节点def __init__(self,data):self.data=dataself.lchild=Noneself.rchild=Noneself.parent=Noneclass sousuo():##二叉搜索树创建def __init__(self,li=None):self.root=Noneif li:for val in li:self.insert_2(val)'''def insert(self,node,val):if not node:node=ercha_tree(val)if val < node.data:node.lchild=self.insert(node.lchild,val)node.lchild.parent=nodeelif val > node.data:node.rchild=self.insert(node.rchild,val)node.rchild.parent=nodereturn node'''def insert_2(self,val):##插入p=self.rootif not p:self.root=ercha_tree(val)returnwhile True:if val<p.data:if p.lchild:p=p.lchildelse:p.lchild=ercha_tree(val)p.lchild.parent=preturnelif val>p.data:if p.rchild:p=p.rchildelse:p.rchild=ercha_tree(val)p.rchild.parent=preturn'''def find(self,val):node=self.rootif not node:return Noneif node.data<val:return self.find(node.rchild,val)elif node.data>val:return self.find(node.rchild,val)else:return node.data'''def find_2(self,val):##查找p=self.rootwhile p:if p.data<val:p=p.rchildelif p.data>val:p=p.lchildelse:return preturn Nonedef mid_read(self,root):##中序遍历if root:self.mid_read(root.lchild)print(root.data, end=' ')self.mid_read(root.rchild)def delete_0(self,node):##叶子节点if not node.parent:self.root=Noneif node==node.parent.lchild:node.parent.child=Noneelse:node.parent.rchild=None##删除操作，分三种情况：def delete_1(self,node):##有左孩子if not node.parent:self.root=Noneif node==node.parent.lchild:node.parent.lchild=node.lchildnode.lchild.parent=node.parentelse:node.parent.rchild=node.lchildnode.lchild.parent=node.parentdef delete_2(self, node):##有右孩子if not node.parent:self.root=Noneif node==node.parent.lchild:node.parnent.lchild=node.rchildnode.rchild.parent=node.parentelse:node.parent.rchild=node.rchildnode.rchild.parent=node.parentdef delete(self,val):if not self.find_2(val):return Noneif self.find_2(val):node=self.find_2(val)if not node.lchild and not node.rchild:self.delete_0(node)elif not node.rchild:self.delete_1(node)elif not node.rchild:self.delete_2(node)else:##有左右孩子，寻找左子树的最大值或者右子树的最小值min_node=node.rchildwhile min_node.lchild:min_node=min_node.lchildnode.data=min_node.dataif min_node.rchild:self.delete_2(min_node)else:self.delete_0(min_node)b=sousuo([5,3,4,7,8])
b.mid_read(b.root)
b.delete(3)
print()
b.mid_read(b.root)

结果：