数据结构-二叉搜索树

article/2025/8/25 0:01:10

目录

二叉搜索树的概念及结构

概念

结构

二叉搜索树的基本操作

默认成员函数

默认构造函数与拷贝构造函数

赋值重载

析构函数

二叉搜索树的插入

非递归

递归

二叉搜索树的遍历

中序遍历---升序（左根右）

中序遍历---降序（右根左）

二叉搜索树的删除

非递归

递归

二叉搜索树的查找

非递归

递归

代码

二叉搜索树的概念及结构

概念

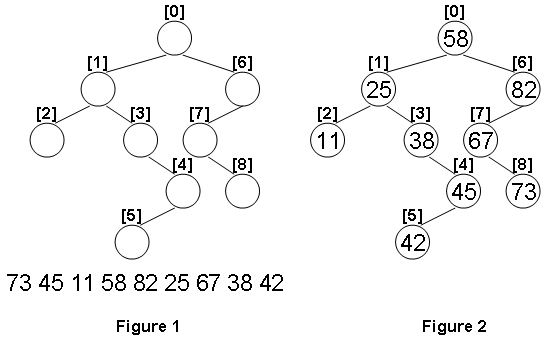
   二叉搜索树也称二叉排序树或者二叉查找树，它是在普通二叉树上加入一些特性所形成的：

  • 1，若左子树非空，则左子树上所有结点的值均小于根结点的值。
  • 2，若右子树非空，则右子树上所有结点的值均大于根结点的值。
  • 3，其左右子树也分别是一棵二叉搜索树。

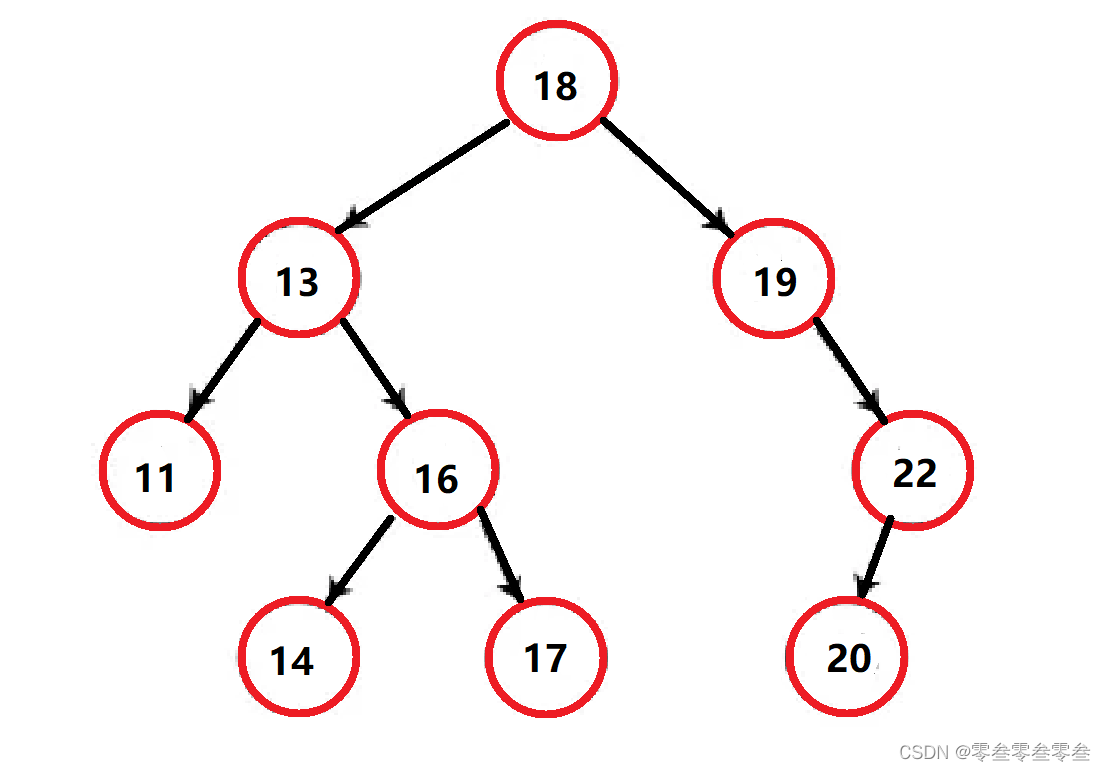
   由二叉搜索树的概念可知，左子树结点值 < 根结点值 < 右子树结点值；所有当二叉搜索树进行中序遍历也就是左根右遍历时，可以得到升序的结果；如果是右根左遍历，就可以得到降序的结果。

结构

   二叉搜索树的物理结构更适合采用链式结构，_left存储比根结点值小的结点地址，_right存储比根结点值大的结点地址。

二叉搜索树的基本操作

   对于二叉搜索树的基本操作，我们选择把它的基本操作与其根结点地址封装到一个类中。

默认成员函数

   二叉搜索树的默认成员函数都需要自己来实现，因为构造与析构涉及到开辟空间与释放空间的操作，而拷贝构造与赋值操作涉及到深拷贝的问题。

默认构造函数与拷贝构造函数

   默认构造函数只需要实现一个无参的构造函数就可以，其作用就是将_root置空。

// 构造BSTree():_root(nullptr) {}

   而拷贝构造函数需要进行深拷贝，就是将被拷贝的二叉搜索树每个结点值拷贝到新开辟结点中，并将新开辟的结点连接成与被拷贝的二叉搜索树结构一样。该拷贝构造过程需要使用到前序遍历的思想，因为先要有双亲结点，才能有左右孩子结点。

// 拷贝构造BSTree(const BSTree& b):_root(_CopyBSTree(b._root)){}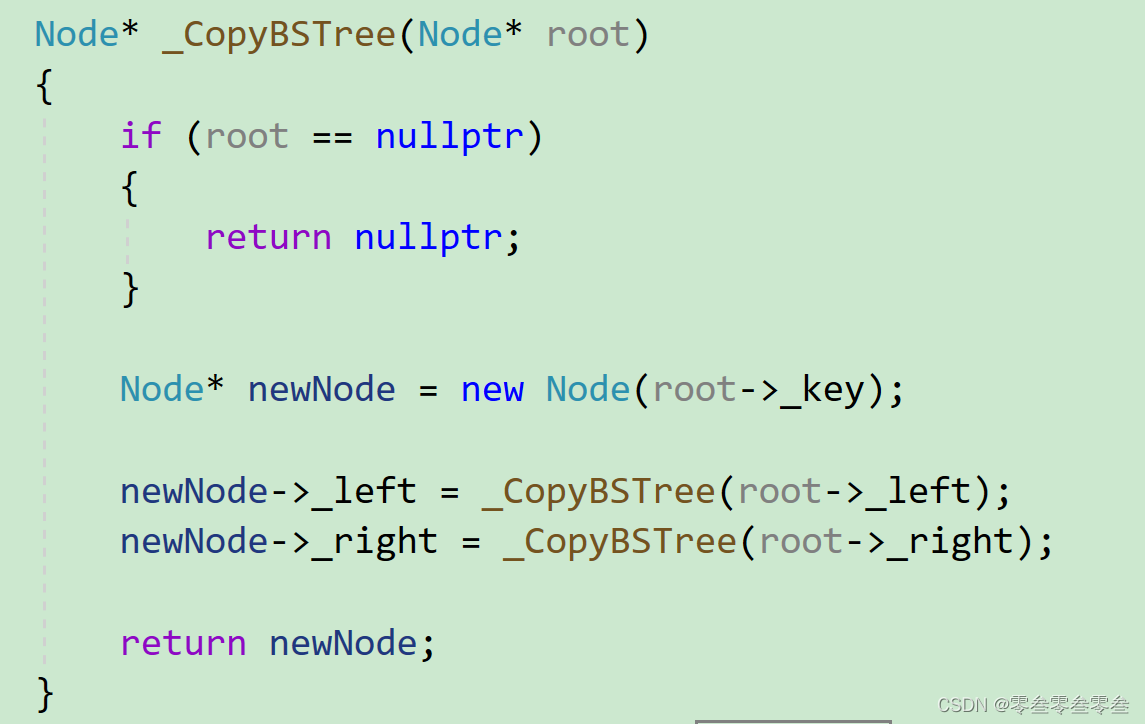

赋值重载

   赋值重载需要利用到拷贝构造，也就是让被拷贝的二叉搜索树拷贝构造一棵新的二叉搜索树，再让这课新树与需要赋值的树进行交换，即完成赋值。

// 赋值重载BSTree<K>& operator=(BSTree<K> b){swap(_root, b._root);return *this;}

析构函数

   析构函数的实现就是通过后序遍历，将二叉搜索树中每一个结点依次释放即可。

// 析构~BSTree(){_DestroyBSTree(_root);_root = nullptr;}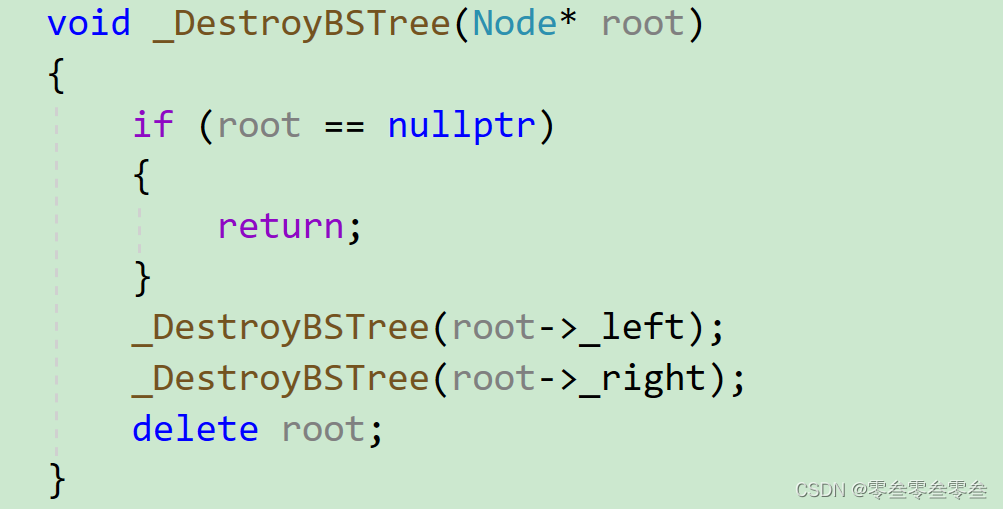

二叉搜索树的插入

   若原二叉搜索树为空树，则直接将新结点插入到根；否则，根据根结点的值进行判断插入，若插入的值小于根，则插入到左子树中，若插入的值大于根，则插入到右子树中。

   需要注意的是，若插入的值在原二叉搜索树中已经存在了，则插入失败；而且插入的这个新结点一定是叶子结点。

非递归

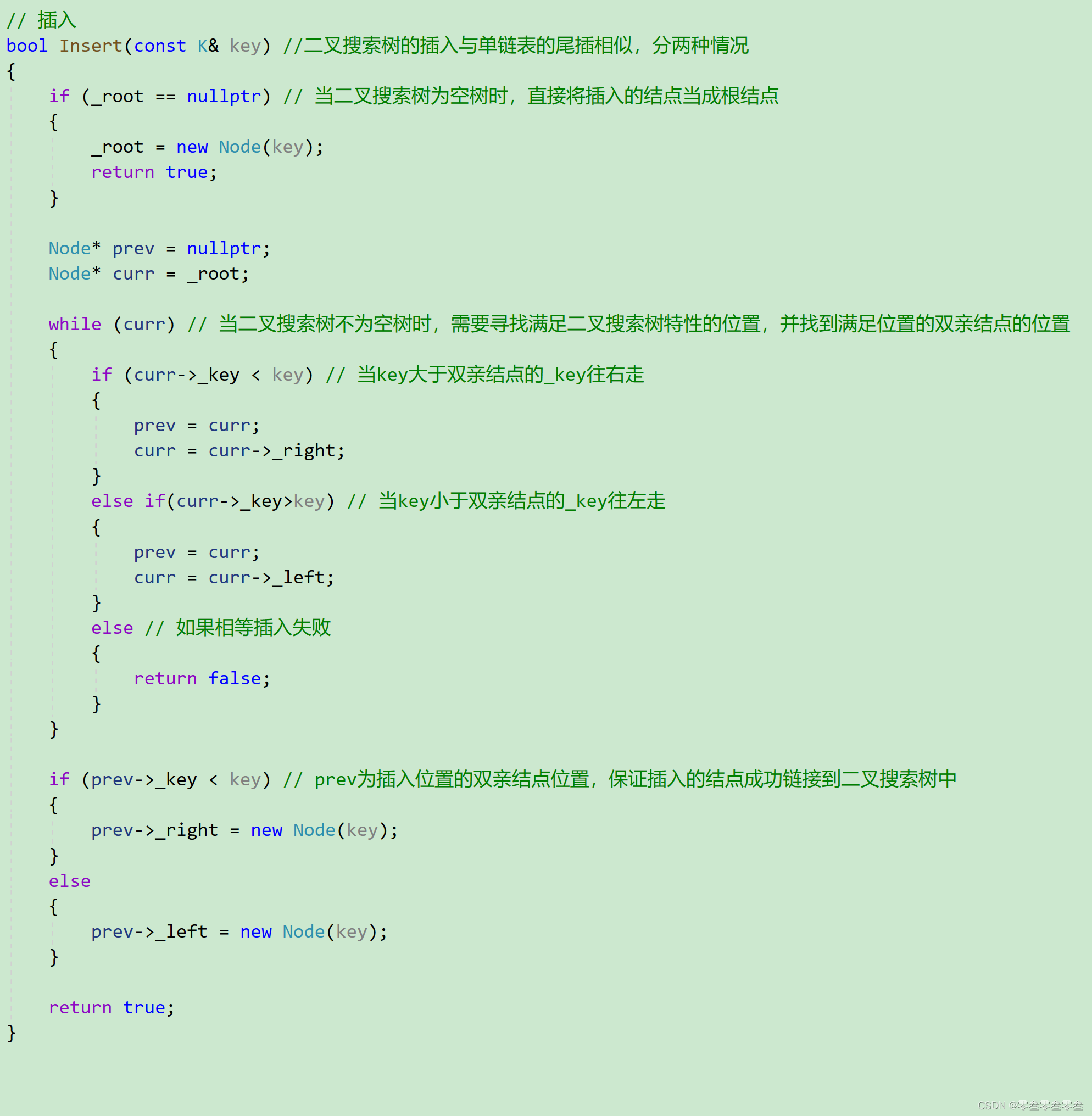
递归

// 插入---递归bool InsertR(const K& key){return _InsertR(_root, key);}

二叉搜索树的遍历

   二叉搜索树的中序遍历是最有意义的。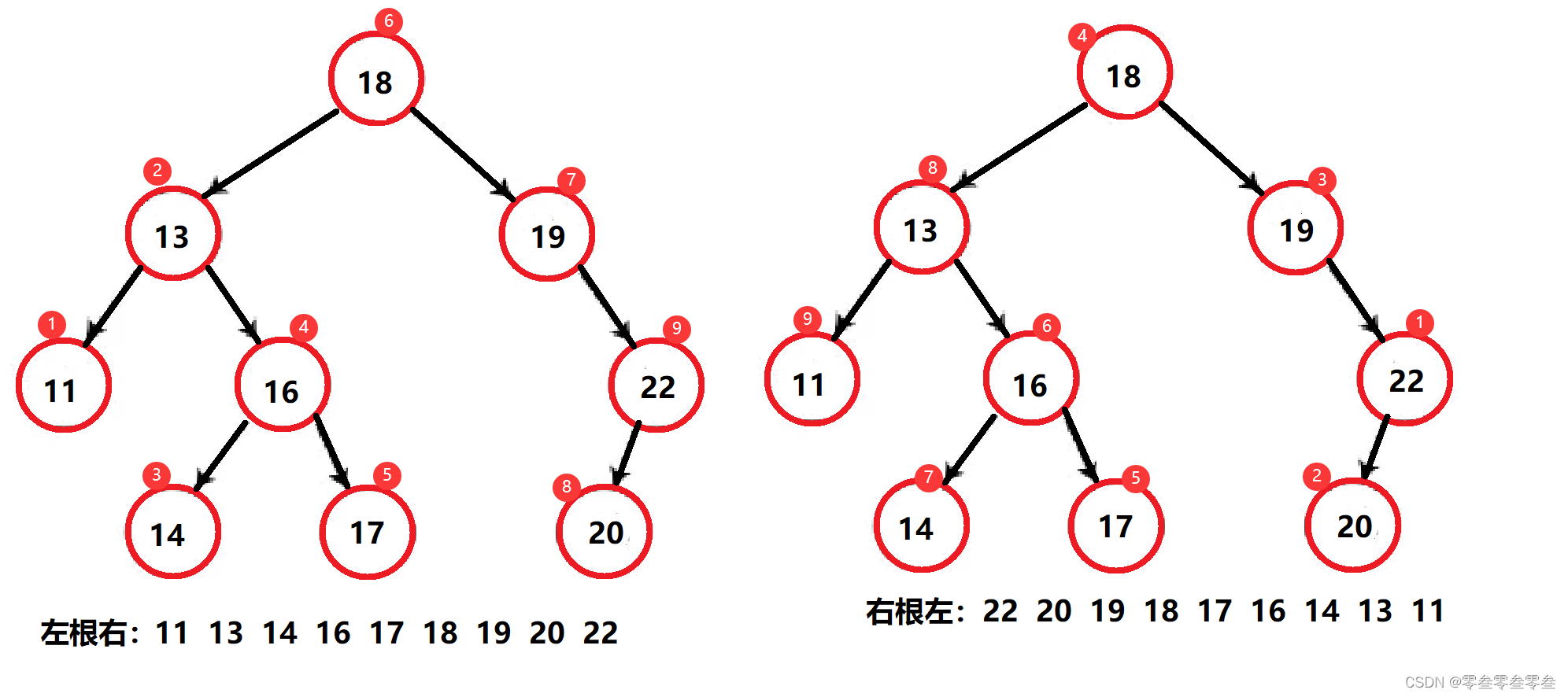

中序遍历---升序（左根右）

void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}// 中序遍历---升序void InOrder(){_InOrder(_root);cout << endl;}

中序遍历---降序（右根左）

void _InOrderReverse(Node* root){if (root == nullptr){return;}_InOrderReverse(root->_right);cout << root->_key << " ";_InOrderReverse(root->_left);}// 中序遍历---降序void InOrderReverse(){_InOrderReverse(_root);cout << endl;}

二叉搜索树的删除

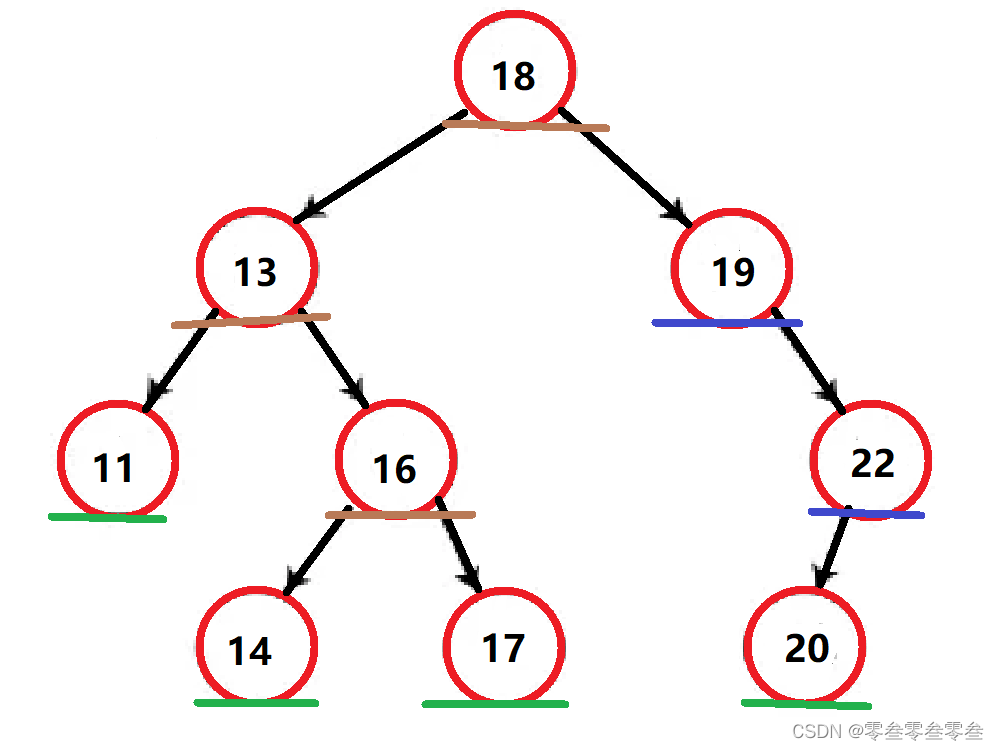   删除分为三种情况：

1，若删除的是11,14,17,20这样的叶子结点，可以直接删除，并将其双亲结点指向自己的指针置空。

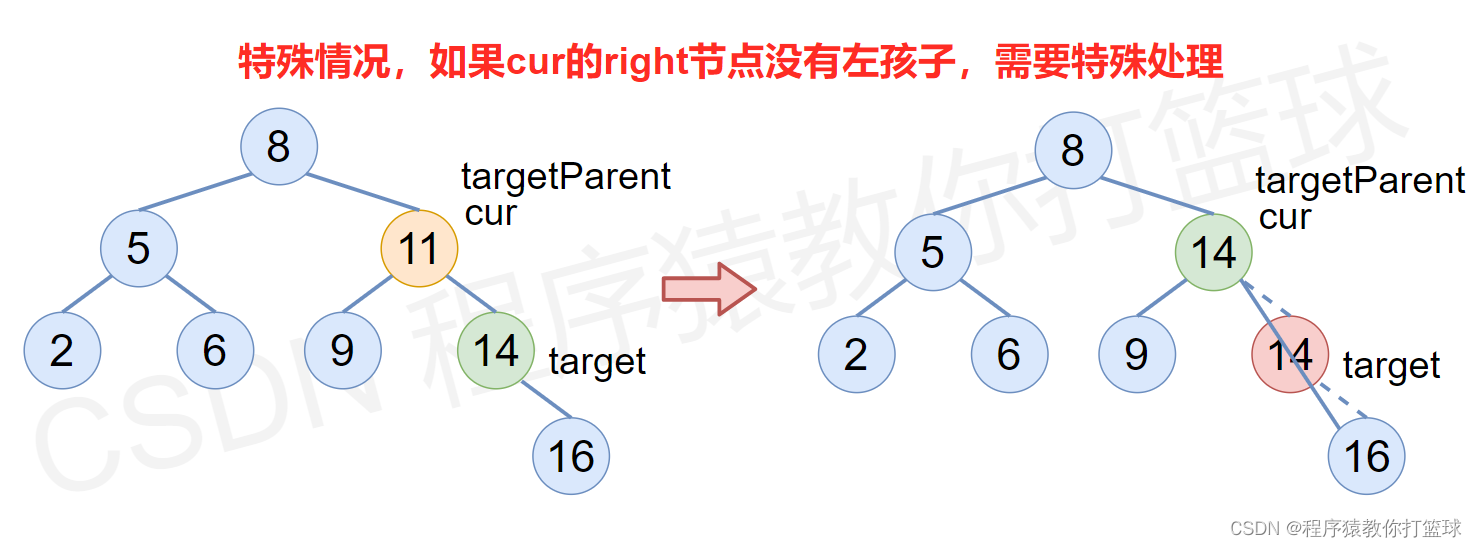
2，若删除的是19,20这样有一个孩子的结点，则可以将自己的孩子给其双亲托管，再删除自己。

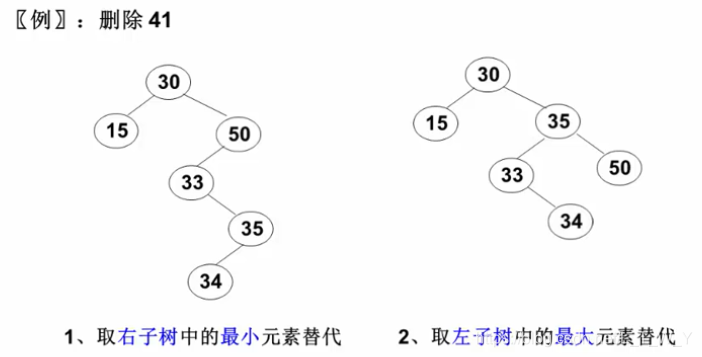
3，若删除的是18,13.16这样有两个孩子的结点，可以使用替换删除法：去要删除结点的左右子树中找到可以顶替自己的结点，也就是在其左子树中找最大的结点或者在其右子树中找最小结点。找到之后保存该结点（该结点的特征与1或者2一样）的值，并删除该结点，最后将保存的值给要删除的结点。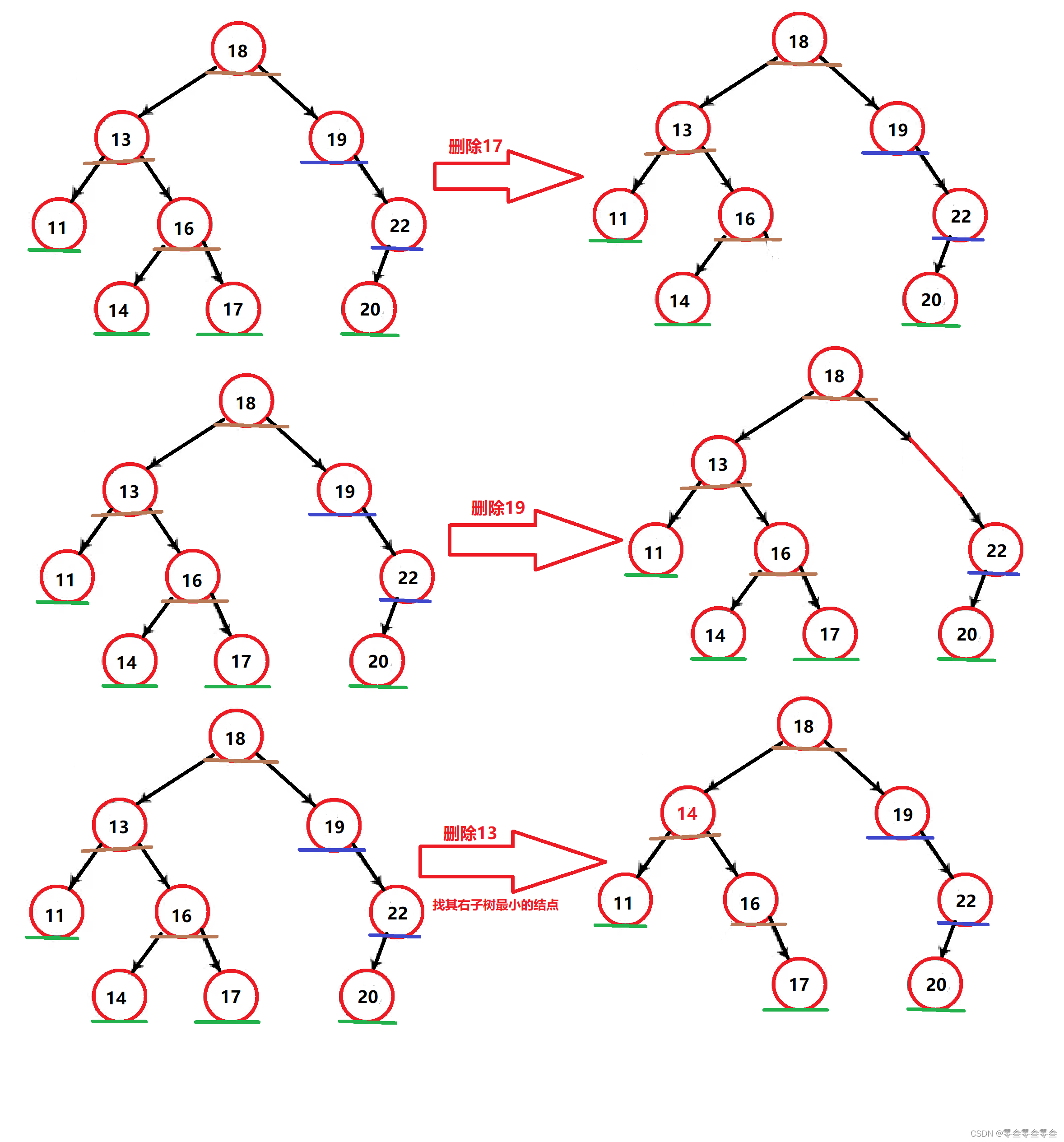

非递归

递归

// 删除---递归bool EraseR(const K& key){return _EraseR(_root, key);}

二叉搜索树的查找

   二叉搜索树的查找就是从根结点开始，沿着某个分支逐层向下比较的过程。先将要查找的值与根结点值比较，如果相等则查找成功；如果不相等，若查找的值小于根结点值，则在根结点的左子树上查找，否则在根结点的右子树上查找；没有找到则返回nullptr。

非递归

递归

// 查找---递归Node* FindR(const K& key){return _FindR(_root, key);}

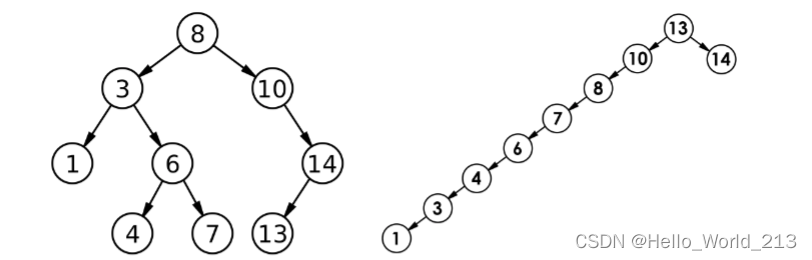
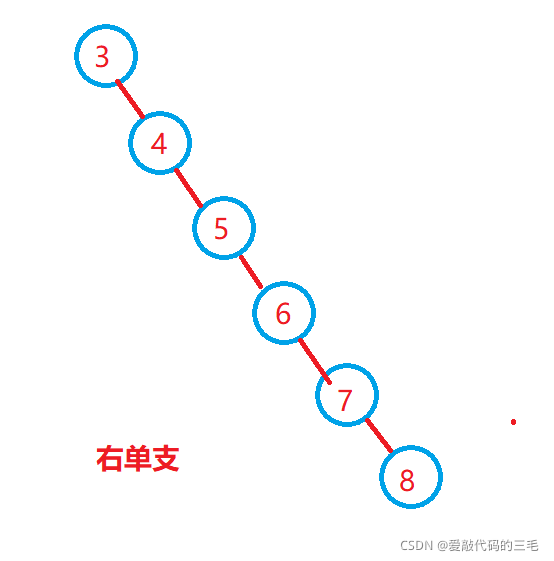
   二叉搜索树的插入删除查找的时间复杂度为O(n)，因为二叉搜索树不能保证自身的结构不是一棵单支树，所以二叉搜索树需要进行优化成AVL树和红黑树。

代码

#pragma once
#include <iostream>
#include <cstdbool>
using namespace std;template <class K>
struct BSTreeNode
{struct BSTreeNode<K>* _left;struct BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key=K()):_left(nullptr),_right(nullptr),_key(key){}
};template <class K>
class BSTree
{typedef struct BSTreeNode<K> Node;private:Node* _root;void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}void _InOrderReverse(Node* root){if (root == nullptr){return;}_InOrderReverse(root->_right);cout << root->_key << " ";_InOrderReverse(root->_left);}bool _InsertR(Node* &root,const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if(root->_key>key){return _InsertR(root->_left, key);}else{return false;}}Node* _FindR(Node* root, const K& key){if (root == nullptr) // 查找失败{return nullptr;}if (root->_key < key) // 大于根结点值，往根结点的右子树上查找{return _FindR(root->_right, key);}else if(root->_key>key) // 小于根结点值，往根结点的左子树上查找{return _FindR(root->_left, key);}else // 查找成功{return root; // 查找成功}}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else // 找到了要删除的结点{if (root->_left == nullptr){Node* del = root;root = root->_right;delete del;return true;}else if(root->_right==nullptr){Node* del = root;root = root->_left;delete del;return true;}else{Node* min = root->_right;while (min->_left){min = min->_left;}K tmp = min->_key;_EraseR(root, tmp);root->_key = tmp;return true;}}}Node* _CopyBSTree(Node* root){if (root == nullptr){return nullptr;}Node* newNode = new Node(root->_key);newNode->_left = _CopyBSTree(root->_left);newNode->_right = _CopyBSTree(root->_right);return newNode;}void _DestroyBSTree(Node* root){if (root == nullptr){return;}_DestroyBSTree(root->_left);_DestroyBSTree(root->_right);delete root;}public: // 构造BSTree():_root(nullptr) {}// 拷贝构造BSTree(const BSTree& b):_root(_CopyBSTree(b._root)){}// 赋值重载BSTree<K>& operator=(BSTree<K> b){swap(_root, b._root);return *this;}// 析构~BSTree(){_DestroyBSTree(_root);_root = nullptr;}// 插入bool Insert(const K& key) //二叉搜索树的插入与单链表的尾插相似，分两种情况{if (_root == nullptr) // 当二叉搜索树为空树时，直接将插入的结点当成根结点{_root = new Node(key);return true;}Node* prev = nullptr;Node* curr = _root;while (curr) // 当二叉搜索树不为空树时，需要寻找满足二叉搜索树特性的位置，并找到满足位置的双亲结点的位置{if (curr->_key < key) // 当key大于双亲结点的_key往右走{prev = curr;curr = curr->_right;}else if(curr->_key>key) // 当key小于双亲结点的_key往左走{prev = curr;curr = curr->_left;}else // 如果相等插入失败{return false;}}if (prev->_key < key) // prev为插入位置的双亲结点位置，保证插入的结点成功链接到二叉搜索树中{prev->_right = new Node(key);}else{prev->_left = new Node(key);}return true;}// 中序遍历---升序void InOrder(){_InOrder(_root);cout << endl;}// 中序遍历---降序void InOrderReverse(){_InOrderReverse(_root);cout << endl;}// 查找Node* Find(const K& key) // 二叉搜索树的查找与单链表的查找相似{Node* curr = _root;while (curr){if (curr->_key < key){curr = curr->_right;}else if (curr->_key > key){curr = curr->_left;}else{return curr;}}return nullptr; // return curr; 也行}// 删除bool Erase(const K&key){Node* prev = nullptr;Node* curr = _root;while (curr) // 寻找值为key的结点，prev为该结点的双亲结点{if (curr->_key < key) // 如果key大于当前结点的_key，则往右走{prev = curr;curr = curr->_right;}else if(curr->_key>key) // 如果key小于当前结点的_key，则往左走{prev = curr;curr = curr->_left;}else // 找到_key为key的结点---该结点分为三类：1，没有左右孩子结点 2，有一个孩子结点 3，左右孩子结点都{if (curr->_left == nullptr) // 如果该结点没有左孩子结点，则需要将该结点的右结点给其双亲结点{if (curr == _root) // 如果删除的是根结点，则将_root改为其右子树{_root = curr->_right;}else {if (prev->_left == curr) // 判断删除的结点是双亲的左孩子还是右孩子{prev->_left = curr->_right;}else{prev->_right = curr->_right;}}delete curr;return true;}else if (curr->_right == nullptr) // 如果该结点没有右孩子结点，则需要将该结点的左结点给其双亲结点{if (curr == _root) // 如果删除的是根结点，则将_root改为其左子树{_root = curr->_left;}else{if (prev->_left == curr)// 判断删除的结点是双亲的左孩子还是右孩子{prev->_left = curr->_left;}else{prev->_right = curr->_left;}}delete curr;return true;}else // 如果删除的结点左右孩子都有，则进行替换删除{/*Node* minPrev = curr; Node* min = curr->_right; // 寻找删除结点的右子树中最小结点while (min->_left){minPrev = min;min = min->_left;}if (minPrev == curr) // 避免最小结点是删除结点的右孩子结点{minPrev->_right = min->_right;}else{minPrev->_left = min->_right;}curr->_key = min->_key;delete min;*/Node* min = curr->_right; // 选出右子树最小的结点while (min->_left){min = min->_left;}K tmp = min->_key; // 保存右子树最小结点的值Erase(tmp); // 将tmp值的结点删除_root->_key = tmp; // 再将tmp的值赋给有两个孩子的结点，想当将这个结点删除return true;}}}return false; // 没有找到删除的结点，则说明删除失败，返回false}// 插入---递归bool InsertR(const K& key){return _InsertR(_root, key);}// 查找---递归Node* FindR(const K& key){return _FindR(_root, key);}// 删除---递归bool EraseR(const K& key){return _EraseR(_root, key);}};

http://chatgpt.dhexx.cn/article/rmuDssn2.shtml

相关文章

二叉搜索树的应用

二叉搜索树的应用

文章目录 1. 二叉搜索树的应用2. 二叉搜索树的KV模型3. 关于const K导致无法erase4. 关于while (cin >> str)5. 面试oj题5.1根据二叉树创建字符串5.2二叉树的层序遍历5.3二叉树的最近公共祖先5.4 二叉搜索树与双向链表5.5从前序与中序遍历序列构造二叉树5.6二叉树的前序遍…
阅读更多...
【C++】二叉搜索树

【C++】二叉搜索树

目录 一、二叉搜索树概念 1、概念 2、结构 3、性质 二、二叉搜索树模拟实现 1、二叉搜索树节点 2、二叉搜索树构造函数 3、二叉搜索树查找 (1)迭代版本 (2)递归版本 4、二叉搜索树插入 (1)迭代版本 (2)递归版本 5、二叉搜索树节点删除 (1)迭代版本 (2)递归版本 …
阅读更多...
Python 二叉搜索树

Python 二叉搜索树

二叉搜索树(BST)&#xff0c;有时也被称为二叉排序树&#xff0c;是一种特殊类型的容器: 在内存中存储“项目”&#xff08;例如数字&#xff0c;名称等&#xff09;的数据结构。它们允许快速查找、添加和删除项目。二叉排序树是带根结点的二叉树&#xff0c;其内部结点各自存储…
阅读更多...
构建二叉搜索树

构建二叉搜索树

二叉搜索树 (BST) 递归定义为具有以下属性的二叉树&#xff1a; 若它的左子树不空&#xff0c;则左子树上所有结点的值均小于它的根结点的值若它的右子树不空&#xff0c;则右子树上所有结点的值均大于或等于它的根结点的值它的左、右子树也分别为二叉搜索树 给定二叉树的具体…
阅读更多...
【Java 数据结构】实现一个二叉搜索树

【Java 数据结构】实现一个二叉搜索树

目录 1、认识二叉搜索树 2、实现一个二叉搜索树 2.1 成员变量 2.2 insert 方法 2.3 search 方法 2.4 remove 方法(重点) 3、二叉搜索树总结 1、认识二叉搜索树 从字面上来看&#xff0c;它只比二叉树多了搜索两个字&#xff0c;我们回想一下&#xff0c;如果要是在二…
阅读更多...
java二叉搜索树详解

java二叉搜索树详解

文章目录 一、概念二、相关操作2.0节点相关代码&#xff1a;2.1查找2.2插入2.3删除&#xff08;重难点&#xff09;2.4测试用例 三、小结 提示&#xff1a;以下是本篇文章正文内容&#xff0c;下面案例可供参考 一、概念 二叉搜索树又称二叉排序树 它或者是一棵空树&#xff…
阅读更多...
二叉搜索树

二叉搜索树

目录 二叉搜索树二叉搜索树概念 增删查改接口插入递归插入查找递归查找删除递归删除 成员函数拷贝构造拷贝赋值析构 二叉搜索树的应用二叉搜索树的性能分析 二叉搜索树 二叉搜索树概念 二叉搜索树又称二叉排序树&#xff0c;它或者是一棵空树&#xff0c;或者是具有以下性质的…
阅读更多...
【数据结构】二叉搜索树

【数据结构】二叉搜索树

目录 一.二叉搜索树规则 二.框架 三.实现 1.查找, 插入, 删除 迭代法实现 递归法实现 2.构造, 赋值 默认构造 拷贝构造 赋值运算符重载 3.中序遍历 四.时间复杂度及稳定性 五.key模型与key/value模型 1.key模型 2.key/value模型 一.二叉搜索树规则 二叉搜索树又…
阅读更多...
数据结构——二叉搜索树详解

数据结构——二叉搜索树详解

二叉搜索树 一、什么是二叉搜索树 二叉搜索树&#xff08;BST&#xff0c;Binary Search Tree&#xff09;&#xff0c;也称二叉排序树或二叉查找树。 二叉搜索树&#xff1a;一棵二叉树&#xff0c;可以为空&#xff1b;如果不为空&#xff0c;满足以下性质&#xff1a; 非空…
阅读更多...
【数据结构】——二叉搜索树

【数据结构】——二叉搜索树

目录 前言 二叉搜索树的概念 二叉搜索树的操作 树的节点实现 搜索树的基本结构 插入数据 查找 删除 拷贝构造函数 二叉搜索树的应用 前言 在c中的容器里map和set的学习需要二叉搜索树的铺垫&#xff0c;也为后边的的红黑树和AVL树做铺垫&#xff0c;也就是说&#xff0c;…
阅读更多...
二叉搜索树(二叉排序树)

二叉搜索树(二叉排序树)

一.概念 二叉搜索树又称二叉排序树&#xff0c;具有以下性质&#xff1a; 若它的左子树不为空&#xff0c;则左子树上所有节点的值都小于根节点的值若它的右子树不为空&#xff0c;则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树 注意&#xff1a;二…
阅读更多...
二叉排序树（二叉查找树、二叉搜索树）（图解+完整代码）

二叉排序树（二叉查找树、二叉搜索树）（图解+完整代码）

目录 ⚽1.什么是二叉排序树 &#x1f3d0;2.构建二叉排序树 &#x1f3c0;3.二叉排序树的查找操作 &#x1f94e;4.二叉排序树的删除 &#x1f3b1;5.完整代码 ⚽1.什么是二叉排序树 我们直接看它的性质&#xff1a; 若它的左子树不空&#xff0c;则左子树上所有结点的值…
阅读更多...
种树：二叉树、二叉搜索树、AVL树、红黑树、哈夫曼树、B树、树与森林

种树：二叉树、二叉搜索树、AVL树、红黑树、哈夫曼树、B树、树与森林

虽然今天不是植树节&#xff0c;但是我今天想种树。 文章目录 树&#xff0c;什么是树&#xff1f;二叉树定义二叉树的创建二叉树的前中后序遍历前序遍历&#xff1a;中序遍历后序遍历已知前序、中序遍历结果&#xff0c;还原二叉树已知后序、中序遍历结果&#xff0c;还原二叉…
阅读更多...
java lrucache_Java LruCache 的使用及原理

java lrucache_Java LruCache 的使用及原理

概述 LRU (Least Recently Used) 的意思就是近期最少使用算法&#xff0c;它的核心思想就是会优先淘汰那些近期最少使用的缓存对象。 在我们日常开发中&#xff0c;UI 界面进行网络图片加载是很正常的一件事情&#xff0c;但是当界面上的图片过于多的时候&#xff0c;不可能每次…
阅读更多...
LruCache和DiskLruCache

LruCache和DiskLruCache

前言 Android中的三级缓存主要就是内存缓存和硬盘缓存。 Lru(least recently used)意为最近最少使用算法&#xff0c;核心思想就是当缓存满时&#xff0c;会优先淘汰最近最少使用的缓存对象。 LruCache的使用 在Android中可以直接使用LruCache&#xff0c;算法原理是&#xff1…
阅读更多...
Android LruCache 缓存

Android LruCache 缓存

使用场景 1、场景一&#xff1a;图片缓存利器。 可以规定缓存大小、有效避免OOM、自动移除队尾不用的图片缓存、避免HashMap各种问题。 2、场景二&#xff1a;通信缓存 从服务端需要获取数据&#xff0c;但是当访问的数据比较大&#xff0c;比较多&#xff0c;并且是重复数…
阅读更多...
Java——LRUCache

Java——LRUCache

概念 简单来说&#xff0c;由于我们的空间是有限的&#xff0c;所以发明了这个数据结构&#xff0c;当我们的空间不够添加新的元素时&#xff0c;就会删除最近最少使用的元素。 其底层逻辑通过哈希表和链表共同实现。哈希表中存储链表的每一个元素&#xff0c;方便进行元素的…
阅读更多...
LruCache缓存

LruCache缓存

Lru算法&#xff1a; Lru 指的是“Least Recently Used-近期最少使用算法”。 1、那么LruCache到底是什么呢&#xff1f; LruCache 是对限定数量的缓存对象持有强引用的缓存&#xff0c;每一次缓存对象被访问&#xff0c;都会被移动到队列的头部。当有对象要被添加到已经达到数…
阅读更多...
LruCache 源码解析

LruCache 源码解析

1. 概述 对于 Android 开发者&#xff0c;LruCache 肯定不陌生&#xff0c;几乎所有的图片缓存框架都会用到它来实现内存缓存等&#xff0c;可见 LruCache 在 Android 开发中的重要性。LRU 是 Least Recently Used 的缩写&#xff0c;近期最少使用的意思。当我们进行缓存的时候…
阅读更多...
LruCache

LruCache

LruCache这个类是通过Glide得知的&#xff0c;不过它是自己又基于LRU算法自己写了个LruCache工具类&#xff0c;不过基本原理类似&#xff0c;都是基于LRU算法实现的 1.来源 一般来说&#xff0c;缓存策略主要包含缓存的添加、获取和删除这三类操作。如何添加和获取缓存这个比…
阅读更多...
推荐文章

Copyright @ 2022~2023