哈夫曼树的基本概念

哈夫曼树通常以二叉树的形式出现，所以也称最优二叉树，是一类带权路径长度最短的树

首先得知道下以下几个术语：

路径：从树中的一个结点到另一个结点之间的分支构成这两点之间的路径

路径长度：路径上的分支数目称作路径长度

树的路径长度：从树根到每一个结点的路径长度之和

权：赋予某个实体的一个量

结点的带权路径长度：从该结点到树根之间的路径长度与结点上权的乘积

树的带权路径长度：树中所有叶子结点的带权路径长度之和

哈夫曼树的构造方法

哈夫曼树的实现利用了贪心算法的理念，就是先给定的若干结点的权进行分割，让它们变为单个的森林或者说是单个的树，因为树肯定是森林，而后在其中选择两个权值最小的结点生成新的结点，而后删除被选择的结点，让生成的结点参与森林中进行选拔，直至无结点进行选拔。

不好意思结点搞的太多了。。。每次生成都是到最后的原因是因为后面的代码，不然最后的结果不是一样的，当然哈夫曼树并不唯一，但是为了让最后答案一样，我选择这样画，这个过程也是后面构建哈夫曼树代码的过程，后面代码看不懂的可以结合这个图一起理解。

接下来就是哈夫曼树的存储结构了，因为每个结点需要权值，孩子结点与双亲结点的地址和结点的数据，所以我们需要用一个结构体来存储。而且这是二叉树的顺序存储。

typedef struct 
{char data;             //结点的数据int parent,lch,rch;    //双亲结点和孩子结点的下标int weight;            //结点的权值
}htNode,*HuffmanTree;

这个就是这个结构体的内部图，有了存储结构后，我们要做的就是初始化，因为是顺序存储，所以我们要知道给的这些结点构成哈夫曼树需要多少空间，因为我们要节省空间，所以需要用动态分配的方法来解决。

而我们知道，假设有n个结点构成哈夫曼树则会生成2n-1个结点，这是因为每个结点都会有个双亲，而根结点没有双亲，生成结点和边数相同为n-1，所以为2n-1，而我们在构成哈夫曼树时0下标是不用的，所以我们真正要申请的空间为2n个。

知道这些后我们就可以来初始化哈夫曼树了，我们在各自输入权值和结点数据后还需把各个结点的孩子与双亲的值置为-1（置为-1的好处就是能当个flag，也就是现在都没有双亲，都是森林，而且在生成的过程中不会出现和它相同的值）：以下是初始化的代码

int initHuffmanTree(huffmanTree& HT)
{HT = (htNode*)malloc(sizeof(htNode) * (2 * NODENUM));			//给HT分配2 * NODENUM个htNOde大小的htNode类型的数组for (int i = 1; i <= 2 * NODENUM - 1; i++)						//下标从1开始到2 * NODENUM{HT[i].parent = HT[i].lch = HT[i].rch = -1;					//双亲和孩子的值都置为-1}printf("please input some weight!\n");for (int i = 1; i <= NODENUM; i++)								//权值只有1-n个{scanf("%d",&HT[i].weight);									//给每个结点赋予权值}char c = getchar();											//这个来接收上面的回车printf("please input some data!\n");for (int i = 1; i <= NODENUM; i++){//scanf("%c ",&HT[i].data);char a = getchar();if(a == '\n')												//遇到回车就结束break;elseHT[i].data = a;											//给每个结点赋予数据}return 1;
}

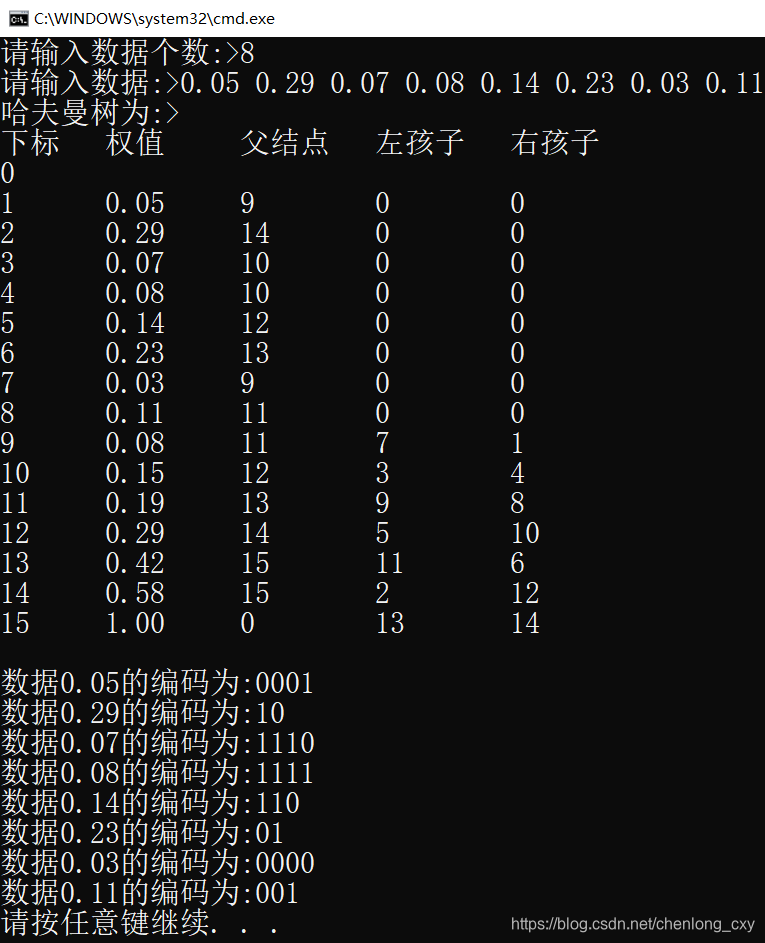
这是初始化后的结果。初始化完后我们就可以开始构建哈夫曼树啦，构建的思想和刚才那张图一样，就是找到最小的两个结点，然后权值相加，然后最小的两个结点的parent的值为新生成结点的下标，新生成结点的孩子的值为两个最小结点的下标。举个例子你就懂了

eq：现在最小的为1，4，则它们相加的结果要放在下标为11的位置，并且parent的值改为11，而11的孩子的值为1，2。更新后如下：

经过n-1次操作后，最终就成了哈夫曼树，下面为最终结果，有颜色的为生成结点部分：

可以直观的看到，在最后一个结点，下标为19parent值为-1，所以这个就是根结点，表示没有双亲。

现在的问题是，我们知道是怎么回事，那怎么用代码来实现它呢

首先先设置2个变量存储最小值，2个变量存储最小值的下标，因为要生成n-1个结点，所以我们要操作n-1次，且生成一次我们要比较的次数就会增加1，而且不难看出来最后一次不用比较了，所以我们比较的次数要比现总结点数小1，按我们的例子来说，我们要生成19个结点，且比较18次，那我们剩下的工作就是如何找最小值并且生成新的结点，我们的逻辑思维应该是利用4个变量去记住值和下标

并且只合并parent为-1的结点，parent不为-1的我们就不用再去判断了，代码如下：

#define MAXVALUE 32767	void creatHuffmanTree(huffmanTree& HT, int n)
{if (n <= 1)															//如果结点数小于等于1，不创建return;int min1, min2;														//定义两个数，来存储每次选取最小两个结点的权值int rnode, lnode;													//定义两个下标值，来存储每次选取最小两个结点的下标for (int i = n + 1; i <= 2 * n -1; i++)								//要生成n-1个结点，所以要操作n—1次且从下标为n+1开始存储{int min1 = MAXVALUE; int lnode = -1;							//让最小值初始化为极大值，这样叶子结点的最大值再大也不会超过这个值了							int min2 = MAXVALUE; int rnode = -1;for (int j = 1; j <= i - 1; j++)								//因为起先是在前n个中选择最小的两个结点的权值，但新生成一个后就得在前n+1个中选择最小的两个结点的权值							{																//假设n = 10 总结点数就得为19，那我们就只要比较18次就可以得出结果了，记住比较的次数比生成的总结点数少1if (HT[j].weight < min1 && HT[j].parent == -1)			//这个小于就使得当出现相同的权值时优先考虑先出现的值，可以假设下{min2 = min1;	rnode = lnode;						//碰到比min1小的，那min1的值就给第二小的min2，下标也给它min1 = HT[j].weight; lnode = j;						//然后最小的给min1，下标同理}else if (HT[j].weight < min2 && HT[j].parent == -1)		//这是第二小的判断{min2 = HT[j].weight;rnode = j;}}HT[lnode].parent = HT[rnode].parent = i;						//最小两个结点的parent变为生成结点的下标HT[i].lch = lnode; HT[i].rch = rnode;							//生成结点的左孩子为最小的min1的下标，右孩子同理HT[i].weight = HT[lnode].weight + HT[rnode].weight;				//生成结点的权值等于最小结点的权值相加}}

在此我给出第一次循环的图示，接下来就是同理了：

构成哈夫曼树就在此结束并完成了，而后就是编码。

哈夫曼编码

哈夫曼编码基于哈夫曼树而产生的一种好编码，具体干嘛的我不说了，百度一下你就知道，因为现在已经很晚了，我想一夜干完，哈哈哈

上面已经完成哈夫曼树的构成了，那么编码就是左子树上的为0，右子树上的为1，再自根结点扫描下来到叶子结点，输出的值就为哈夫曼编码。

那我们第一步得确定装编码的存储结构，可以从图中看出，需要一个大数组装很多装编码的小数组，那我们就选择指针数组，因为指针变量就类似一个数组，指针数组是装指针的数组，那就符合我们的需求了。

typedef char** huffmanCode;	//第一个*是代表它是指针变量，说明它是数组//第二个*说明它是指针数组，代表这个char类型数组里每个元素都是*huffmanCode变量

那我们的思路就是搞个临时数组把编码记录下来，然后再给这个大数组里的小数组，那我们怎么求编码呢，这就用到刚才看到那个最后一个结点的parent了，因为它的值是-1，所以它被我们定义为根结点，所以我们只要顺着parent存着的下标一步一步找上去就行了，而后就是左孩子为0，右孩子为1。下面为代码：

void createHuffmanCode(huffmanTree HT, huffmanCode& HC, int n)
{HC = (huffmanCode)malloc(sizeof(huffmanCode) * n + 1);				//申请n + 1个huffmanCode大小huffmanCode类型的临时空间//因为下标是从一开始，所以我们要申请比结点多一个的结点，和哈夫曼树的结构对应，方便输出char* cd = (char*)malloc(sizeof(char) * n);							//申请n个char大小char类型的临时空间，这个临时数组记录每次遍历出来的编码int start = 0,c = 0,f = 0;											//start为cd数组记录下标，c初始为叶子结点下标，而后就是孩子结点的下标，f记录双亲结点的下标cd[n - 1] = '\0';													//这个就是给printf留着的，因为printf不会生成'\0'，如果用puts就不用这句语句了for (int i = 1; i <= n; i++)										//只要叶子结点的编码{start = n - 1;													//这句要赋值n的话，start--要写在判断后方c = i;f = HT[c].parent;while (f != -1)													//根节点没有双亲{start--;if (HT[f].lch == c)											//是左孩子就是0，右孩子就为1cd[start] = '0';elsecd[start] = '1';c = f; f = HT[c].parent;									//向根结点接近}HC[i] = (char*)malloc(sizeof(char) * (n - start));				//给数组里的数组申请n - start个char大小的char*类型的临时空间strcpy(HC[i], &cd[start]);										//cd里记录的编码给HC的第i个数组}free(cd);															//释放临时空间
}

出一个循环的图，这图画的我累死。

全部代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <malloc.h>
#include <string.h>
#define MAXVALUE 32767		//极大值相当于无穷大
#define NODENUM 10			//叶子结点数
typedef struct
{char data;				//数据域int weight;				//结点的权值int parent, lch, rch;	//双亲与孩子的下标
}htNode,*huffmanTree;		typedef char** huffmanCode;	//第一个*是代表它是指针变量，说明它是数组//第二个*说明它是指针数组，代表这个char类型数组里每个元素都是*huffmanCode变量int initHuffmanTree(huffmanTree& HT);								//初始化哈夫曼树
void creatHuffmanTree(huffmanTree& HT, int n);						//构建哈夫曼树
void createHuffmanCode(huffmanTree HT, huffmanCode &HC, int n);		//编写哈夫曼编码
int main()
{huffmanTree HT ;initHuffmanTree(HT);huffmanCode HC;creatHuffmanTree(HT,NODENUM);createHuffmanCode(HT,HC,NODENUM);/*for (int i = NODENUM + 1; i <= 2 * NODENUM - 1; i++)printf("%d ", HT[i].weight);*/for (int i = 1; i <= NODENUM; i++)								//遍历输出编码{printf("%c:\t",HT[i].data);printf("%s\n", HC[i]);}return 0;
}
int initHuffmanTree(huffmanTree& HT)
{HT = (htNode*)malloc(sizeof(htNode) * (2 * NODENUM));			//给HT分配2 * NODENUM个htNOde大小的htNode类型的数组for (int i = 1; i <= 2 * NODENUM - 1; i++)						//下标从1开始到2 * NODENUM{HT[i].parent = HT[i].lch = HT[i].rch = -1;					//双亲和孩子的值都置为-1}printf("please input some weight!\n");for (int i = 1; i <= NODENUM; i++)								//权值只有1-n个{scanf("%d",&HT[i].weight);									//给每个结点赋予权值}char c = getchar();											//这个来接收上面的回车printf("please input some data!\n");for (int i = 1; i <= NODENUM; i++){//scanf("%c ",&HT[i].data);char a = getchar();if(a == '\n')												//遇到回车就结束break;elseHT[i].data = a;											//给每个结点赋予数据}return 1;
}void creatHuffmanTree(huffmanTree& HT, int n)
{if (n <= 1)															//如果结点数小于等于1，不创建return;int min1, min2;														//定义两个数，来存储每次选取最小两个结点的权值int rnode, lnode;													//定义两个下标值，来存储每次选取最小两个结点的下标for (int i = n + 1; i <= 2 * n -1; i++)								//要生成n-1个结点，所以要操作n—1次且从下标为n+1开始存储{int min1 = MAXVALUE; int lnode = -1;							//让最小值初始化为极大值，这样叶子结点的最大值再大也不会超过这个值了							int min2 = MAXVALUE; int rnode = -1;for (int j = 1; j <= i - 1; j++)								//因为起先是在前n个中选择最小的两个结点的权值，但新生成一个后就得在前n+1个中选择最小的两个结点的权值							{																//假设n = 10 总结点数就得为19，那我们就只要比较18次就可以得出结果了，记住比较的次数比生成的总结点数少1if (HT[j].weight < min1 && HT[j].parent == -1)			//这个小于就使得当出现相同的权值时优先考虑先出现的值，可以假设下{min2 = min1;	rnode = lnode;						//碰到比min1小的，那min1的值就给第二小的min2，下标也给它min1 = HT[j].weight; lnode = j;						//然后最小的给min1，下标同理}else if (HT[j].weight < min2 && HT[j].parent == -1)		//这是第二小的判断{min2 = HT[j].weight;rnode = j;}}HT[lnode].parent = HT[rnode].parent = i;						//最小两个结点的parent变为生成结点的下标HT[i].lch = lnode; HT[i].rch = rnode;							//生成结点的左孩子为最小的min1的下标，右孩子同理HT[i].weight = HT[lnode].weight + HT[rnode].weight;				//生成结点的权值等于最小结点的权值相加}}void createHuffmanCode(huffmanTree HT, huffmanCode& HC, int n)
{HC = (huffmanCode)malloc(sizeof(huffmanCode) * n + 1);				//申请n + 1个huffmanCode大小huffmanCode类型的临时空间//因为下标是从一开始，所以我们要申请比结点多一个的结点，和哈夫曼树的结构对应，方便输出char* cd = (char*)malloc(sizeof(char) * n);							//申请n个char大小char类型的临时空间，这个临时数组记录每次遍历出来的编码int start = 0,c = 0,f = 0;											//start为cd数组记录下标，c初始为叶子结点下标，而后就是孩子结点的下标，f记录双亲结点的下标cd[n - 1] = '\0';													//这个就是给printf留着的，因为printf不会生成'\0'，如果用puts就不用这句语句了for (int i = 1; i <= n; i++)										//只要叶子结点的编码{start = n - 1;													//这句要赋值n的话，start--要写在判断后方c = i;	f = HT[c].parent;while (f != -1)													//根节点没有双亲{start--;if (HT[f].lch == c)											//是左孩子就是0，右孩子就为1cd[start] = '0';elsecd[start] = '1';c = f; f = HT[c].parent;									//向根结点接近}HC[i] = (char*)malloc(sizeof(char) * (n - start));				//给数组里的数组申请n - start个char大小的char*类型的临时空间strcpy(HC[i], &cd[start]);										//cd里记录的编码给HC的第i个数组}free(cd);															//释放临时空间
}