文章目录
- 哈夫曼树的基本概念
- 哈夫曼树的构建
- 构建思路
- 代码实现
- 哈夫曼编码的生成
- 编码生成思路
- 代码实现
- 完整代码展示以及代码测试
哈夫曼树的基本概念
在认识哈夫曼树之前,你必须知道以下几个基本术语:
1、什么是路径?
在一棵树中,从一个结点往下可以达到的结点之间的通路,称为路径。
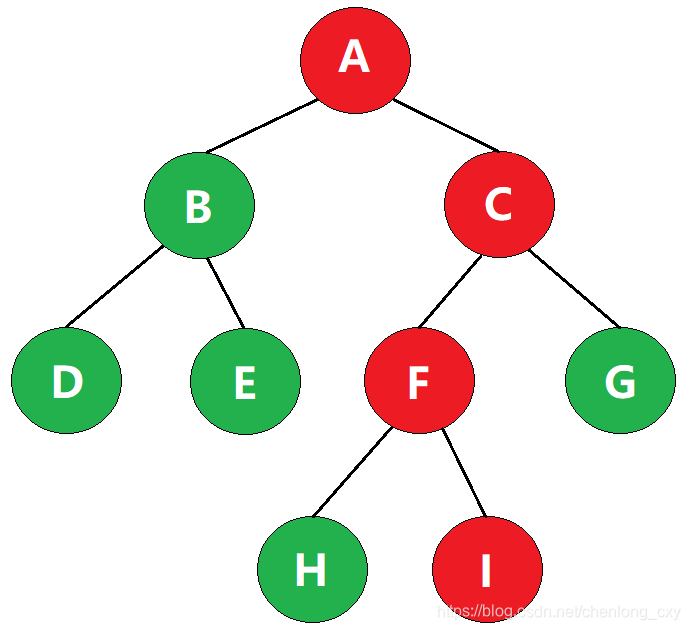
如图,从根结点A到叶子结点I的路径就是A->C->F->I
2、什么是路径长度?
某一路径所经过的“边”的数量,称为该路径的路径长度
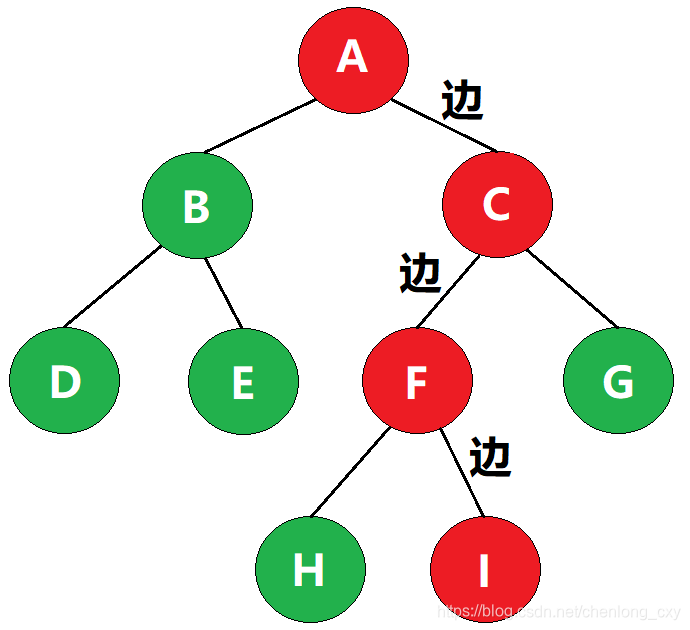
如图,该路径经过了3条边,因此该路径的路径长度为3
3、什么是结点的带权路径长度?
若将树中结点赋给一个带有某种含义的数值,则该数值称为该结点的权。从根结点到该结点之间的路径长度与该结点的权的乘积,称为该结点的带权路径长度。
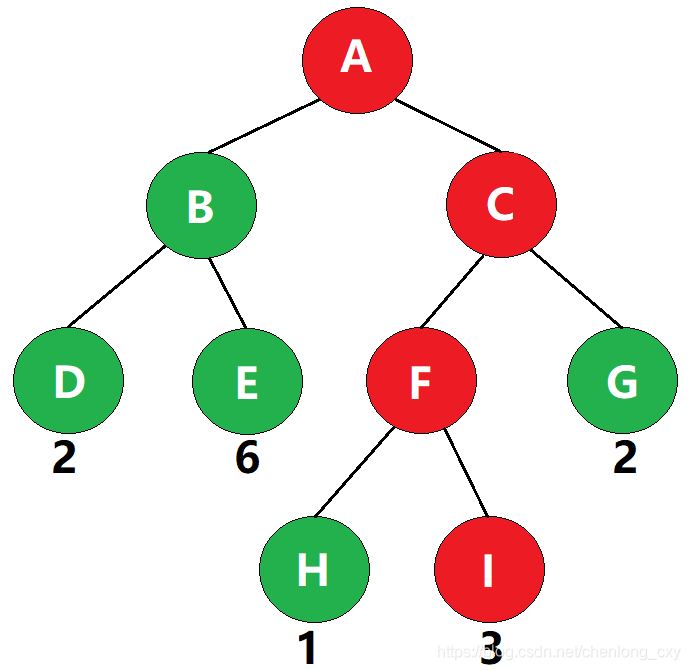
如图,叶子结点I的带权路径长度为 3 × 3 = 9 3\times3=9 3×3=9
4、什么是树的带权路径长度?
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
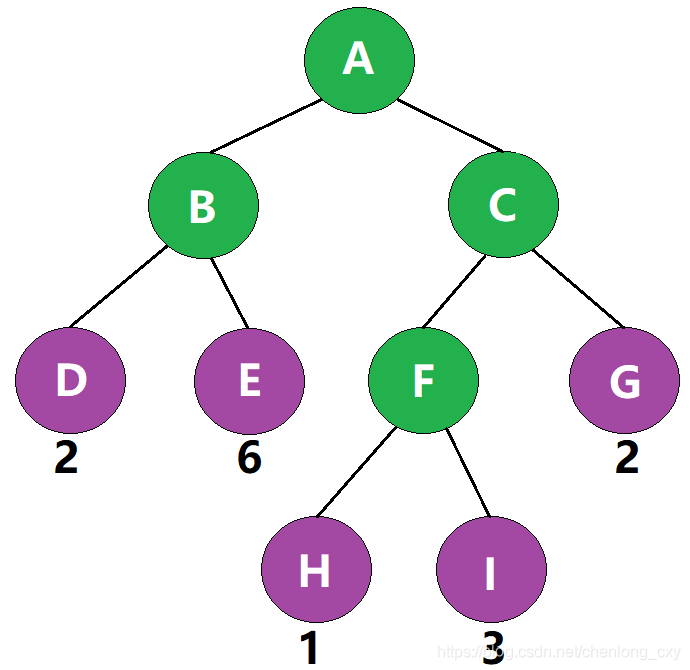
如图,该二叉树的带权路径长度 WPL = 2 × 2 + 2 × 6 + 3 × 1 + 3 × 3 + 2 × 2 = 32 =2\times 2 + 2 \times 6 + 3 \times 1 + 3 \times 3 + 2 \times 2 = 32 =2×2+2×6+3×1+3×3+2×2=32
5、什么是哈夫曼树?
给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,则称该二叉树为哈夫曼树,也被称为最优二叉树。
根据树的带权路径长度的计算规则,我们不难理解:树的带权路径长度与其叶子结点的分布有关。
即便是两棵结构相同的二叉树,也会因为其叶子结点的分布不同,而导致两棵二叉树的带权路径长度不同。
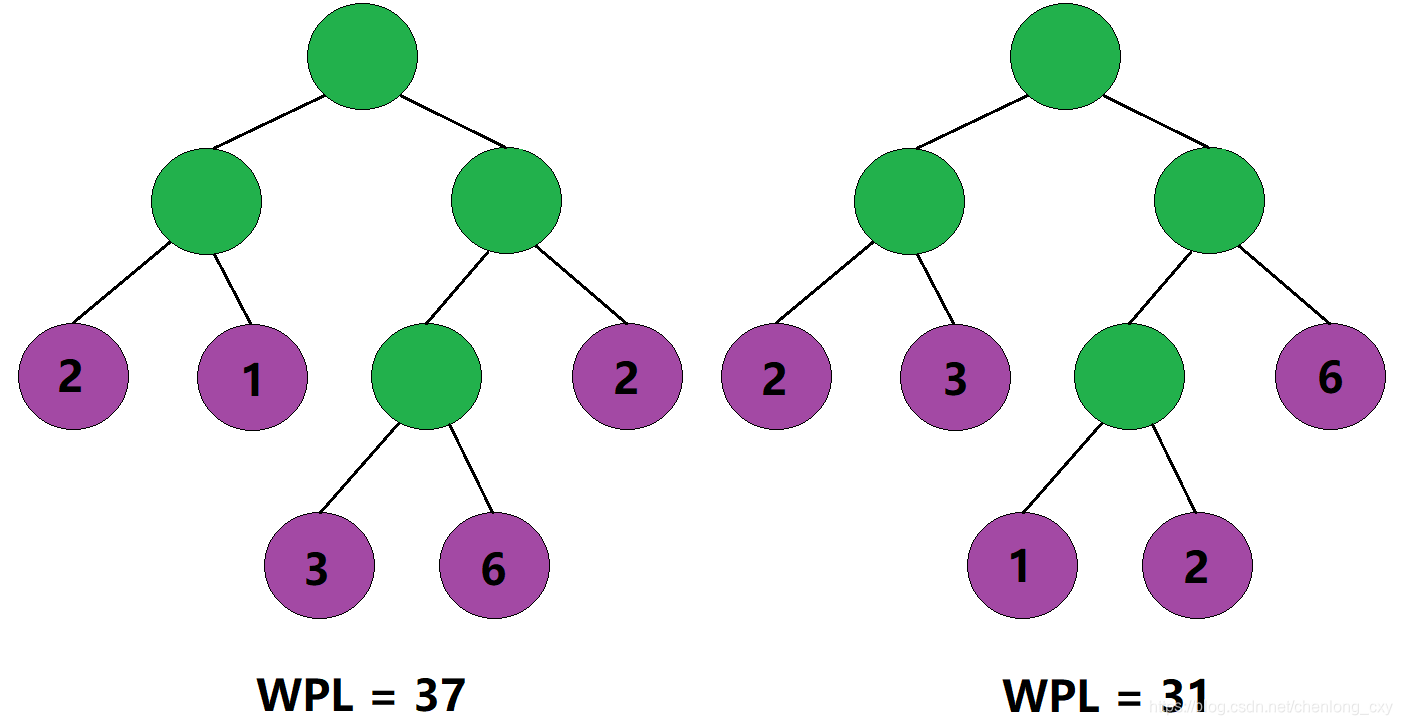
那如何才能使一棵二叉树的带权路径长度达到最小呢?
根据树的带权路径长度的计算规则,我们应该尽可能地让权值大的叶子结点靠近根结点,让权值小的叶子结点远离根结点,这样便能使得这棵二叉树的带权路径长度达到最小。
哈夫曼树的构建
构建思路
下面给出一个非常简洁易操作的算法,来构造一棵哈夫曼树:
1、初始状态下共有n个结点,结点的权值分别是给定的n个数,将他们视作n棵只有根结点的树。
2、合并其中根结点权值最小的两棵树,生成这两棵树的父结点,权值为这两个根结点的权值之和,这样树的数量就减少了一个。
3、重复操作2,直到只剩下一棵树为止,这棵树就是哈夫曼树。
例如,现给定5个数,分别为1、2、2、3、6,要求构建一棵哈夫曼树。
动图演示:

1、初始状态:有5棵只有根结点的树。

2、合并权值为1和2的两棵树,生成这两棵树的父结点,父结点权值为3。
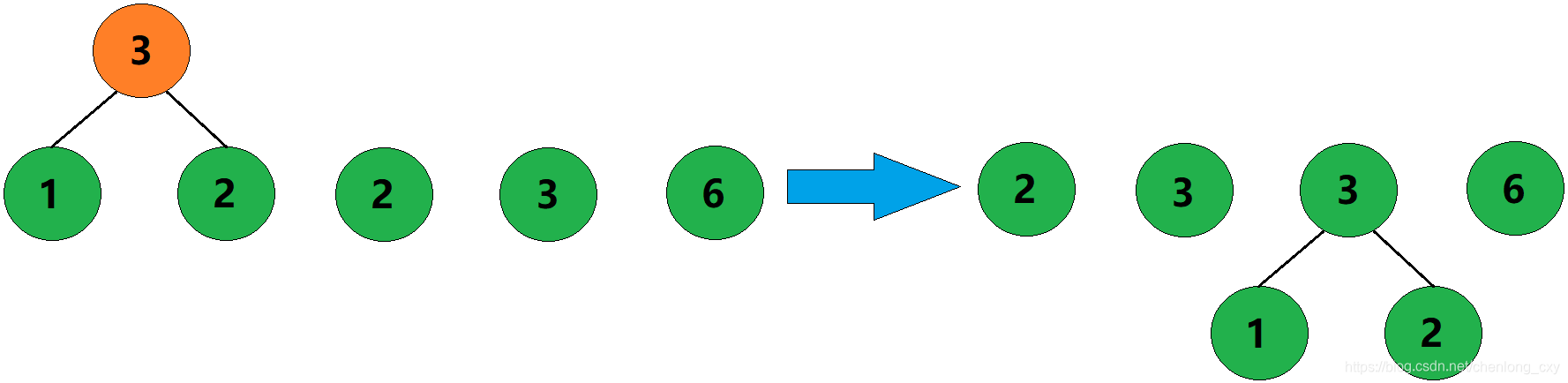
3、合并权值为2和3的两棵树,生成这两棵树的父结点,父结点权值为5。
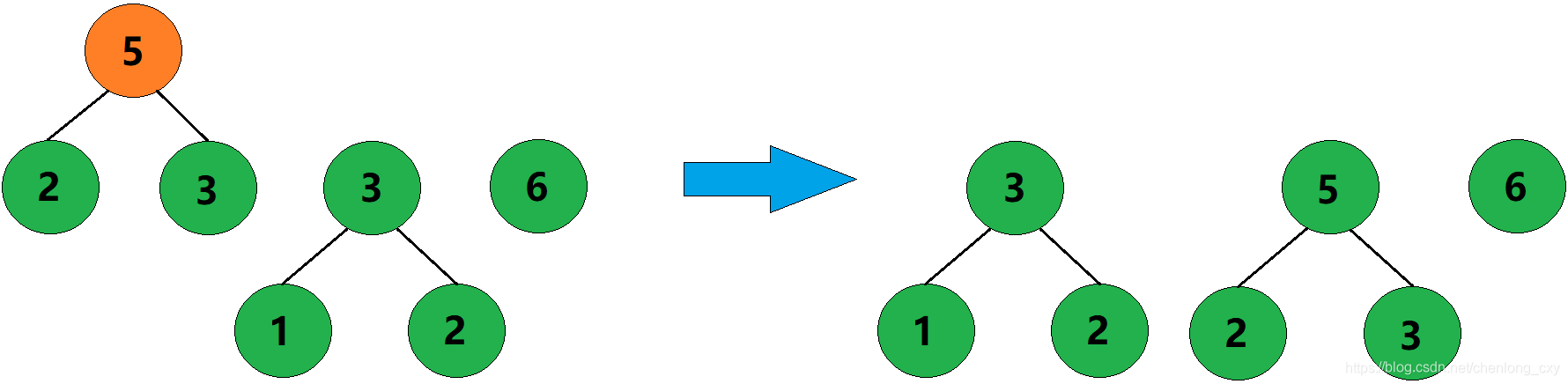
4、合并权值为3和5的两棵树,生成这两棵树的父结点,父结点权值为8。
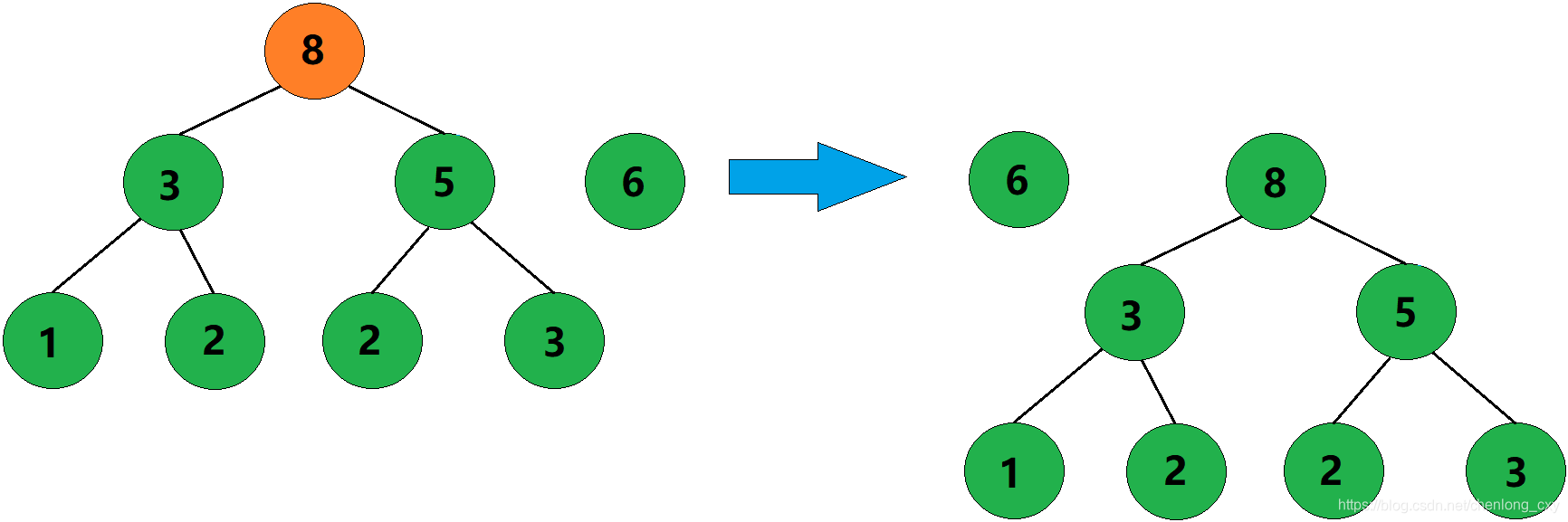
5、合并权值为6和8的两棵树,生成这两棵树的父结点,父结点权值为14。
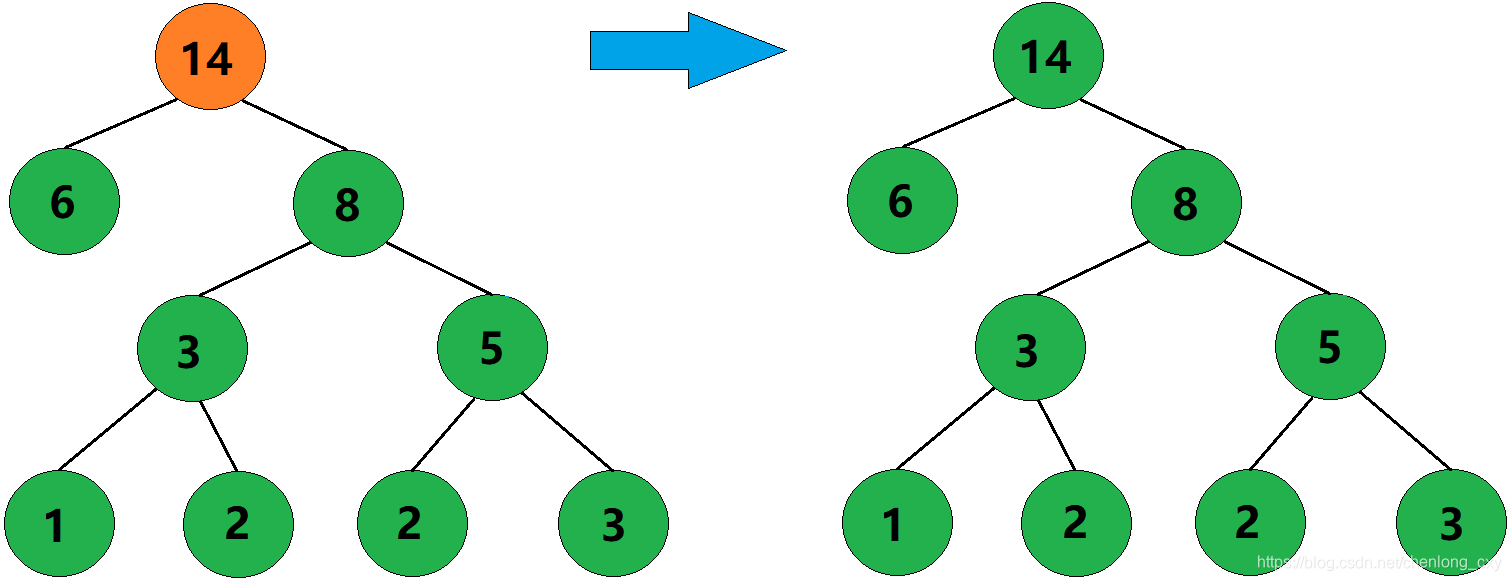
6、此时只剩下一棵树了,这棵树就是哈夫曼树。
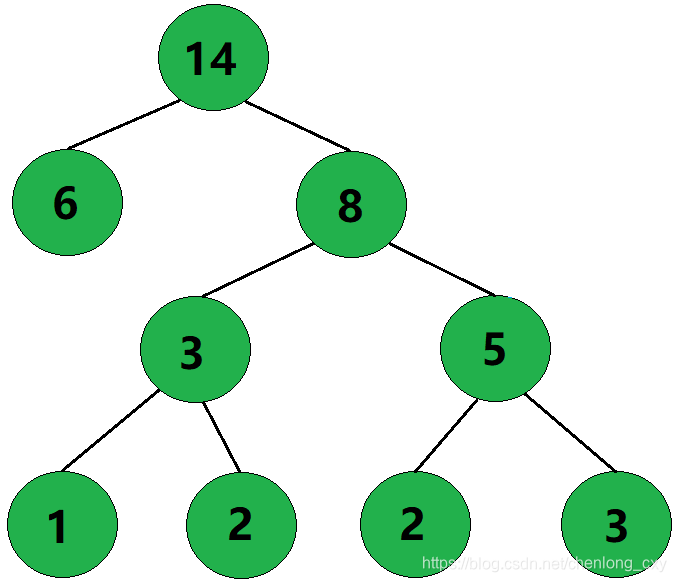
观察这棵哈夫曼树,我们还可以发现,哈夫曼树不存在度为1的结点。因为我们每次都是选择两棵树进行合并,自然不存在度为1的结点。
由此我们还可以推出,若给定n个数要求构建哈夫曼树,则构建出来的哈夫曼树的结点总数为2n-1,因为对于任意的二叉树,其度为0的叶子结点个数一定比度为2的结点个数多1。
证明:
设度为0,1,2的结点个数分别为n0,n1,n2
则二叉树的总结点数 n = n 0 + n 1 + n 2 n=n0+n1+n2 n=n0+n1+n2
设二叉树中边的条数为B
则 B = n 2 × 2 + n 1 × 1 B=n2\times2+n1\times1 B=n2×2+n1×1
又 ∵ B = n − 1 \because B=n-1 ∵B=n−1
∴ n 2 × 2 + n 1 = n − 1 \therefore n2\times2+n1=n-1 ∴n2×2+n1=n−1
即 n = n 2 × 2 + n 1 + 1 n=n2\times2+n1+1 n=n2×2+n1+1
∴ n 0 + n 1 + n 2 = n 2 × 2 + n 1 + 1 \therefore n0+n1+n2 = n2\times2+n1+1 ∴n0+n1+n2=n2×2+n1+1
即 n 0 = n 2 + 1 n0=n2+1 n0=n2+1
总结一下:构建哈夫曼树就是反复选择两个最小的元素进行合并,直到只剩下一个元素为止。
代码实现
代码实现中,单个结点的类型定义如下:
typedef double DataType; //结点权值的数据类型typedef struct HTNode //单个结点的信息
{DataType weight; //权值int parent; //父节点int lc, rc; //左右孩子
}*HuffmanTree;
代码实现时,我们用一个数组存储构建出来的哈夫曼树中各个结点的基本信息(权值、父结点、左孩子以及右孩子)。该数组的基本布局如下:
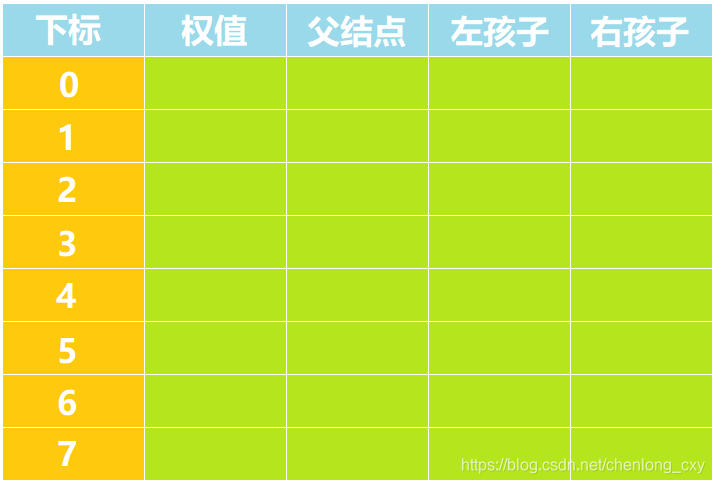
我们以“用数字7、5、4、2构建一棵哈夫曼树”为例,代码的基本实现步骤如下:
第一阶段:
所构建的哈夫曼树的总结点个数为 2 × 4 − 1 = 7 2\times4-1=7 2×4−1=7,但是这里我们开辟的数组可以存储8个结点的信息,因为数组中下标为0的位置我们不存储结点信息,具体原因后面给出。
我们先将用于构建哈夫曼树的数字7、5、4、2依次赋值给数组中下标为1-4的权值位置,其余信息均初始化为0。
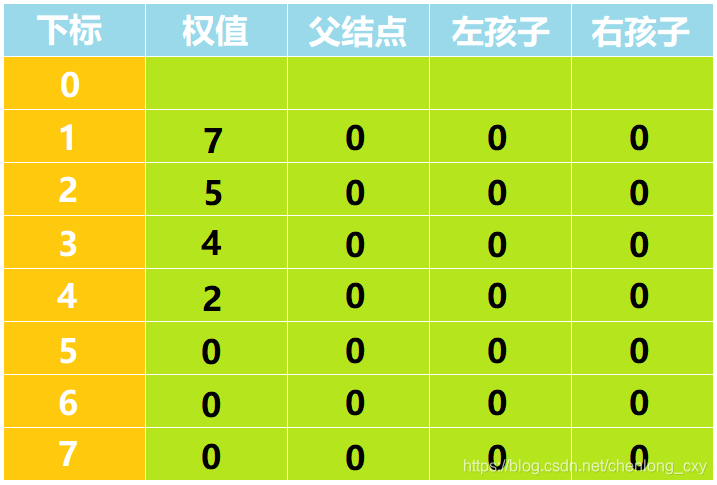
第二阶段:
从数组中下标为1-4的元素中,选取权值最小,并且父结点为0(代表其还没有父结点)的两个结点,生成它们的父结点:
1、下标为5的结点的权值等于被选取的两个结点的权值之和。
2、两个被选取的结点的父结点就是下标为5的结点。
3、下标为5的结点左孩子是被选取的两个结点中权值较小的结点,另外一个是其右孩子。

再从数组中下标为1-5的元素中,选取权值最小,并且父结点为0的两个结点,生成它们的父结点。

继续从数组中下标为1-6的元素中,选取权值最小,并且父结点为0的两个结点,生成它们的父结点。

此时,除了下标为0的元素以外,数组中所有元素均已有了自己的结点信息,哈夫曼树已经构建完毕。
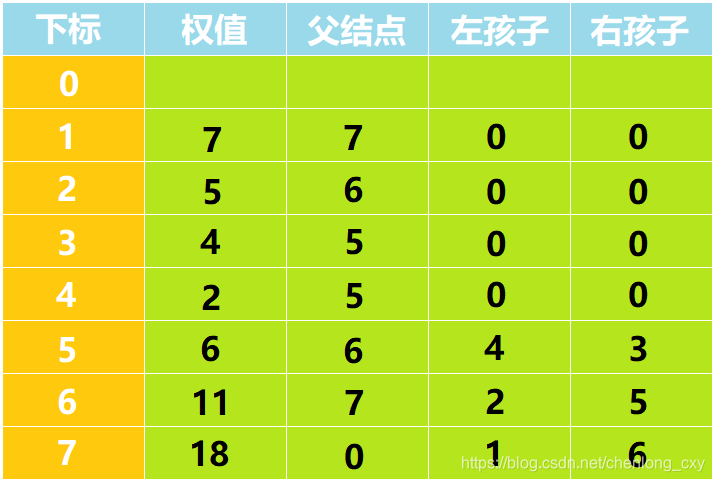
根据数组信息,我们可以画出所构建的哈夫曼树:
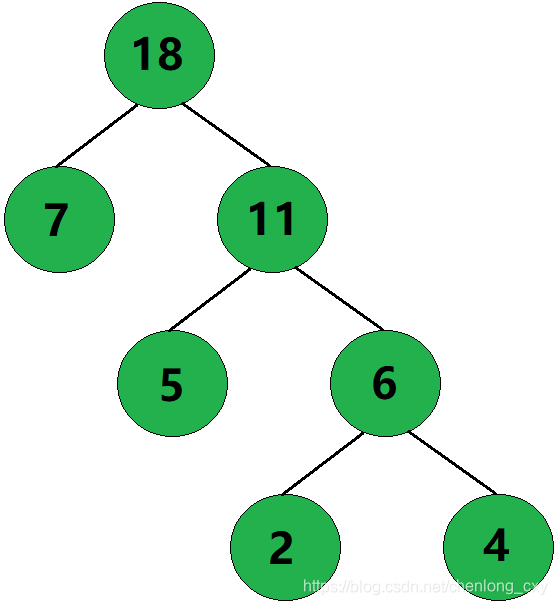
观察该数组中的数据,我们可以发现,权值为7、5、4、2的结点的左孩子和右孩子均为0,也就是它们没有左右孩子,因为它们是叶子结点。此外,数组中父结点为0的结点其实就是所构建的哈夫曼树的根结点。
现在我们来说说为什么数组中下标为0的元素不存储结点信息?
因为在数组中叶子结点的左右孩子是0,根结点的父结点是0,我们若是用数组中下标为0元素存储结点信息,那么我们将不能区分左右孩子为0的结点是叶子结点还是说该结点的左右孩子是下标为0的结点,同时也不知道哈夫曼树的根结点到底是谁。
代码如下:
//在下标为1到i-1的范围找到权值最小的两个值的下标,其中s1的权值小于s2的权值
void Select(HuffmanTree& HT, int n, int& s1, int& s2)
{int min;//找第一个最小值for (int i = 1; i <= n; i++){if (HT[i].parent == 0){min = i;break;}}for (int i = min + 1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight)min = i;}s1 = min; //第一个最小值给s1//找第二个最小值for (int i = 1; i <= n; i++){if (HT[i].parent == 0 && i != s1){min = i;break;}}for (int i = min + 1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight&&i != s1)min = i;}s2 = min; //第二个最小值给s2
}//构建哈夫曼树
void CreateHuff(HuffmanTree& HT, DataType* w, int n)
{int m = 2 * n - 1; //哈夫曼树总结点数HT = (HuffmanTree)calloc(m + 1, sizeof(HTNode)); //开m+1个HTNode,因为下标为0的HTNode不存储数据for (int i = 1; i <= n; i++){HT[i].weight = w[i - 1]; //赋权值给n个叶子结点}for (int i = n + 1; i <= m; i++) //构建哈夫曼树{//选择权值最小的s1和s2,生成它们的父结点int s1, s2;Select(HT, i - 1, s1, s2); //在下标为1到i-1的范围找到权值最小的两个值的下标,其中s1的权值小于s2的权值HT[i].weight = HT[s1].weight + HT[s2].weight; //i的权重是s1和s2的权重之和HT[s1].parent = i; //s1的父亲是iHT[s2].parent = i; //s2的父亲是iHT[i].lc = s1; //左孩子是s1HT[i].rc = s2; //右孩子是s2}//打印哈夫曼树中各结点之间的关系printf("哈夫曼树为:>\n");printf("下标 权值 父结点 左孩子 右孩子\n");printf("0 \n");for (int i = 1; i <= m; i++){printf("%-4d %-6.2lf %-6d %-6d %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lc, HT[i].rc);}printf("\n");
}
注:为了避免使用二级指针,函数传参使用了C++中的引用传参。
哈夫曼编码的生成
编码生成思路
对于任意一棵二叉树来说,把二叉树上的所有分支都进行编号,将所有左分支都标记为0,所有右分支都标记为1。
我们就以7、5、4、2构建的哈夫曼树为例。
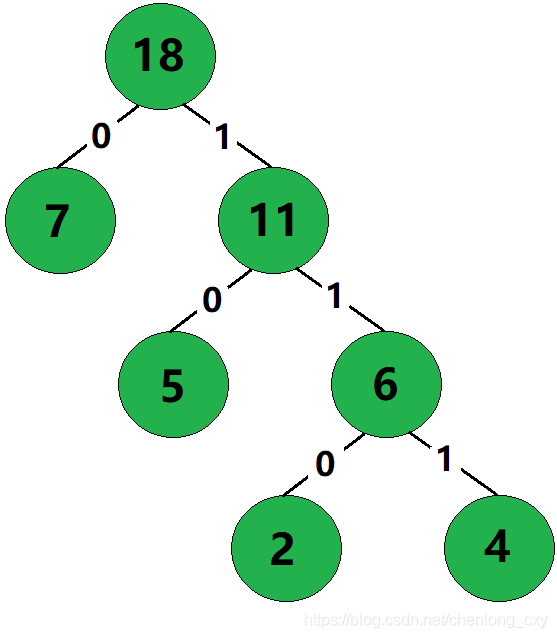
那么对于树上的任何一个结点,都可以根据从根结点到该结点的路径唯一确定一个编号。
对于哈夫曼树上的叶子结点,根据从根结点到该叶子结点的路径所确定的一个编号,就是该叶子结点的哈夫曼编码。
例如,上图中:
叶子结点7的哈夫曼编码为:0
叶子结点5的哈夫曼编码为:10
叶子结点4的哈夫曼编码为:111
叶子结点2的哈夫曼编码为:110
代码实现
我们首先需要清楚这样一个问题:
用n个数据所构建出来的哈夫曼树,生成的哈夫曼编码的长度最长是多少?
因为哈夫曼编码是根据从根结点到该叶子结点的路径所确定的一个编号,所以生成的哈夫曼编码最长的叶子结点一定是离根结点最远的结点。要使叶子结点里根结点达到最远,那么生成的哈夫曼树应该是斜二叉树。
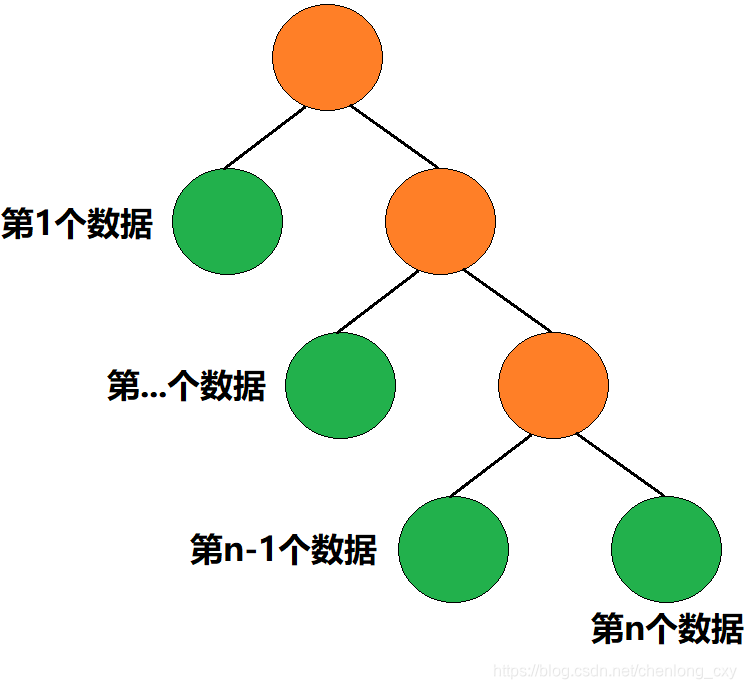
该斜二叉树中最后一层的叶子结点所生成的哈夫曼编码就是最长的,其哈夫曼编码的长度就是从根结点到达该叶子结点的路径长度,即 n − 1 n-1 n−1。
一个字符串若是想要容纳下“用n个数据生成的哈夫曼编码”中的任意一个编码,那么这个字符串的长度应该为 n n n,因为我们还需要用一个字节的位置用于存放字符串的结束标志’\0’。
我们就以数字7、5、4、2构建的哈夫曼树为例,哈夫曼编码生成的基本实现步骤如下:
第一阶段:
因为数据个数为4,所以我们开辟一个大小为4的辅助空间,并将最后一个位置赋值为’\0’,用于暂时存放正在生成的哈夫曼编码。

为了存放这4个数据哈夫曼编码,我们开辟一个字符指针数组,该数组中有5个元素,每个元素的类型为char**,该字符指针数组的基本布局如下:

注意:这里为了与“构建哈夫曼树时所生成的数组”中的下标相对应,所以该字符指针数组中下标为0的元素也不存储有效数据。
第二阶段:
利用已经构建好的哈夫曼树,生成这4个数据的哈夫曼编码。单个数据生成哈夫曼编码的过程如下:
1、判断该数据结点与其父结点之间的关系,若该数据结点是其父结点的左孩子,则将start指针前移,并将0填入start指向的位置,若是右孩子,则在该位置填1。
2、接着用同样的方法判断其父结点与其父结点的父结点之间的关系,直到待判断的结点为哈夫曼树的根结点为止,该结点的哈夫曼编码生成完毕。
3、将字符串中从start的位置开始的数据拷贝到字符指针数组中的相应位置。
这里我们以生成数据5的哈夫曼编码为例。

注意:在每次生成数据的哈夫曼编码之前,先将start指针指向’\0’。
按照此方式,依次生成7、5、4、2的哈夫曼编码后,字符指针数组的基本布局如下:
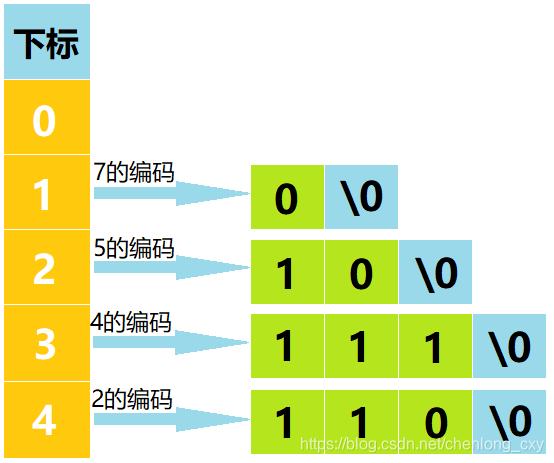
哈夫曼编码生成完毕。
代码如下:
typedef char **HuffmanCode;//生成哈夫曼编码
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n)
{HC = (HuffmanCode)malloc(sizeof(char*)*(n + 1)); //开n+1个空间,因为下标为0的空间不用char* code = (char*)malloc(sizeof(char)*n); //辅助空间,编码最长为n(最长时,前n-1个用于存储数据,最后1个用于存放'\0')code[n - 1] = '\0'; //辅助空间最后一个位置为'\0'for (int i = 1; i <= n; i++){int start = n - 1; //每次生成数据的哈夫曼编码之前,先将start指针指向'\0'int c = i; //正在进行的第i个数据的编码int p = HT[c].parent; //找到该数据的父结点while (p) //直到父结点为0,即父结点为根结点时,停止{if (HT[p].lc == c) //如果该结点是其父结点的左孩子,则编码为0,否则为1code[--start] = '0';elsecode[--start] = '1';c = p; //继续往上进行编码p = HT[c].parent; //c的父结点}HC[i] = (char*)malloc(sizeof(char)*(n - start)); //开辟用于存储编码的内存空间strcpy(HC[i], &code[start]); //将编码拷贝到字符指针数组中的相应位置}free(code); //释放辅助空间
}
注:为了避免使用二级指针,函数传参使用了C++中的引用传参。
完整代码展示以及代码测试
完整源代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef double DataType; //结点权值的数据类型typedef struct HTNode //单个结点的信息
{DataType weight; //权值int parent; //父节点int lc, rc; //左右孩子
}*HuffmanTree;typedef char **HuffmanCode; //字符指针数组中存储的元素类型//在下标为1到i-1的范围找到权值最小的两个值的下标,其中s1的权值小于s2的权值
void Select(HuffmanTree& HT, int n, int& s1, int& s2)
{int min;//找第一个最小值for (int i = 1; i <= n; i++){if (HT[i].parent == 0){min = i;break;}}for (int i = min + 1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight)min = i;}s1 = min; //第一个最小值给s1//找第二个最小值for (int i = 1; i <= n; i++){if (HT[i].parent == 0 && i != s1){min = i;break;}}for (int i = min + 1; i <= n; i++){if (HT[i].parent == 0 && HT[i].weight < HT[min].weight&&i != s1)min = i;}s2 = min; //第二个最小值给s2
}//构建哈夫曼树
void CreateHuff(HuffmanTree& HT, DataType* w, int n)
{int m = 2 * n - 1; //哈夫曼树总结点数HT = (HuffmanTree)calloc(m + 1, sizeof(HTNode)); //开m+1个HTNode,因为下标为0的HTNode不存储数据for (int i = 1; i <= n; i++){HT[i].weight = w[i - 1]; //赋权值给n个叶子结点}for (int i = n + 1; i <= m; i++) //构建哈夫曼树{//选择权值最小的s1和s2,生成它们的父结点int s1, s2;Select(HT, i - 1, s1, s2); //在下标为1到i-1的范围找到权值最小的两个值的下标,其中s1的权值小于s2的权值HT[i].weight = HT[s1].weight + HT[s2].weight; //i的权重是s1和s2的权重之和HT[s1].parent = i; //s1的父亲是iHT[s2].parent = i; //s2的父亲是iHT[i].lc = s1; //左孩子是s1HT[i].rc = s2; //右孩子是s2}//打印哈夫曼树中各结点之间的关系printf("哈夫曼树为:>\n");printf("下标 权值 父结点 左孩子 右孩子\n");printf("0 \n");for (int i = 1; i <= m; i++){printf("%-4d %-6.2lf %-6d %-6d %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lc, HT[i].rc);}printf("\n");
}//生成哈夫曼编码
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n)
{HC = (HuffmanCode)malloc(sizeof(char*)*(n + 1)); //开n+1个空间,因为下标为0的空间不用char* code = (char*)malloc(sizeof(char)*n); //辅助空间,编码最长为n(最长时,前n-1个用于存储数据,最后1个用于存放'\0')code[n - 1] = '\0'; //辅助空间最后一个位置为'\0'for (int i = 1; i <= n; i++){int start = n - 1; //每次生成数据的哈夫曼编码之前,先将start指针指向'\0'int c = i; //正在进行的第i个数据的编码int p = HT[c].parent; //找到该数据的父结点while (p) //直到父结点为0,即父结点为根结点时,停止{if (HT[p].lc == c) //如果该结点是其父结点的左孩子,则编码为0,否则为1code[--start] = '0';elsecode[--start] = '1';c = p; //继续往上进行编码p = HT[c].parent; //c的父结点}HC[i] = (char*)malloc(sizeof(char)*(n - start)); //开辟用于存储编码的内存空间strcpy(HC[i], &code[start]); //将编码拷贝到字符指针数组中的相应位置}free(code); //释放辅助空间
}//主函数
int main()
{int n = 0;printf("请输入数据个数:>");scanf("%d", &n);DataType* w = (DataType*)malloc(sizeof(DataType)*n);if (w == NULL){printf("malloc fail\n");exit(-1);}printf("请输入数据:>");for (int i = 0; i < n; i++){scanf("%lf", &w[i]);}HuffmanTree HT;CreateHuff(HT, w, n); //构建哈夫曼树HuffmanCode HC;HuffCoding(HT, HC, n); //构建哈夫曼编码for (int i = 1; i <= n; i++) //打印哈夫曼编码{printf("数据%.2lf的编码为:%s\n", HT[i].weight, HC[i]);}free(w);return 0;
}
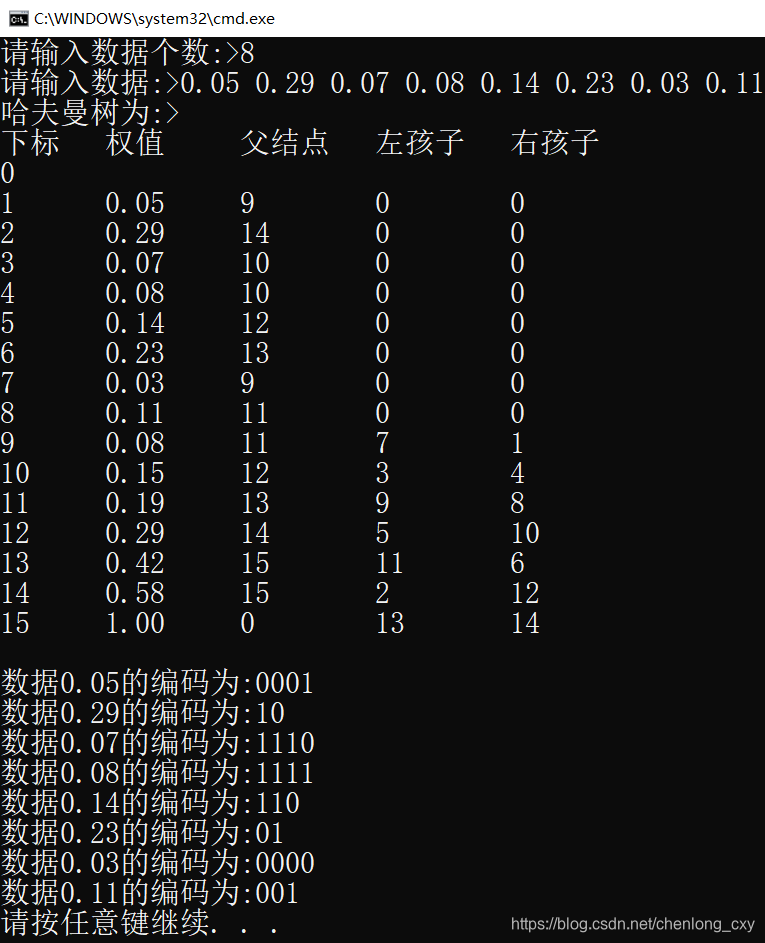
我们就以下问题作为测试:
已知某系统在通信网络中只可能出现八种字符,其概率分别为
0.05,0.29,0.07,0.08,0.14,0.23,0.03,0.11
试设计哈夫曼编码
运行结果: