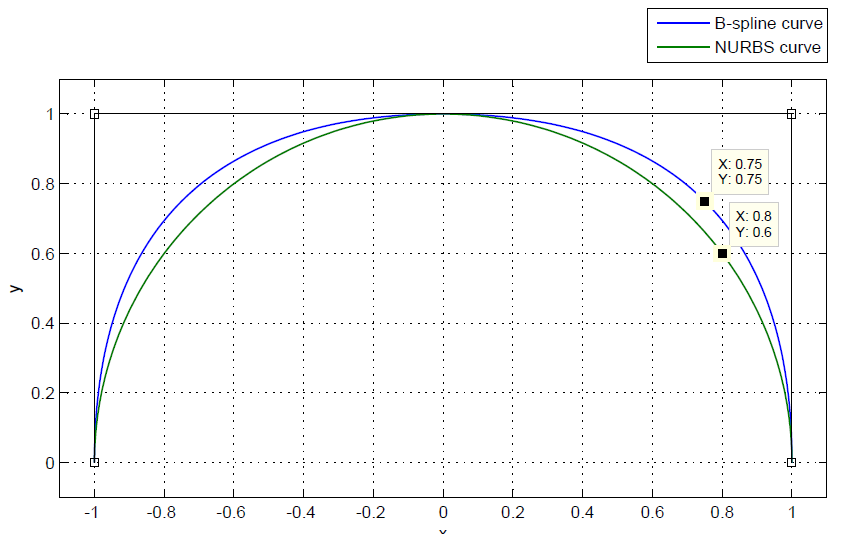
道理相通,我简单分享下在.net MVC下的实装。
1.制作Model类
using System;
using System.Collections.Generic;
using System.Linq;
using System.Web;
namespace RCRS.WebApp.LG.EM.Models
{
//----------------------------------------------------------------
/// /// Import画面用
///
//----------------------------------------------------------------
public class tmp_UploadFile
{
///
public HttpPostedFileBase FileName { get; set; }
}
}
2.实装controller里的对应方法,我这个处理逻辑比较复杂,懒得修改了,反正就这个意思
public virtual ActionResult UploadFile()
{
HttpPostedFileBase uploadedFile = Request.Files["FileName"];
string message = "アップロード失敗しました。";
bool isUploaded = false;
string path = "";
string dateTimeNow = DateTime.Now.ToString("yyMMdd-hhmmss");
string userName = User.Identity.GetUserName();
string uploadMsg = string.Empty;
if (uploadedFile != null && uploadedFile.ContentLength != 0)
{
string pathForSaving = Server.MapPath("~/App_Data/Uploaded/");
try
{
if (BsnssBihin.IsExcel(uploadedFile.FileName))
{
path = System.IO.Path.Combine(pathForSaving, dateTimeNow + "_" + uploadedFile.FileName);
uploadedFile.SaveAs(path);
isUploaded = BsnssBihin.UploadBihinChange(path, userName, ref uploadMsg);
if (isUploaded)
{
message = "アップロード成功しました!" + "\n" + uploadMsg;
Logger.Info("[成功]備品アップロード, " + dateTimeNow + ", " + "[" + userName + "]" + "[" + path + "]" + uploadMsg);
}
else
{
message = "アップロード失敗しました。" + "\n" + uploadMsg;
Logger.Info("[失敗]備品アップロード, " + dateTimeNow + ", " + "[" + userName + "]" + "["+path + "]" + uploadMsg);
}
}
else
{
message = "ファイルの形式は不正です。";
}
}
catch (Exception ex)
{
message = string.Format("失敗しました: {0}", ex.Message);
Logger.Info("[失敗]備品アップロード: " + ex.Message + dateTimeNow + ", " + "[" + userName + "]" + "[" + path + "]");
}
}
return Json(new { isUploaded = isUploaded, message = message }, "text/html");
}
3.页面的实装
@model RCRS.WebApp.LG.EM.Models.tmp_UploadFile
選 択
@Html.TextBoxFor(m => m.FileName, new { id = "file-upload", type = "file", accept = "application/vnd.openxmlformats-officedocument.spreadsheetml.sheet, application/vnd.ms-excel" })
処理中、少々お待ちください

@section scripts{
@Scripts.Render("~/bundles/jquery")
@Scripts.Render("~/bundles/jqueryui")
@Scripts.Render("~/bundles/jqueryval")
@Scripts.Render("~/bundles/common")
@Scripts.Render("~/bundles/fileupload")
}
就是这个样子
还附赠了一个简易loding的实现
贴出CSS代码:
.dvloader {
display:none;
position:absolute;
top:40%;
left:40%;
width:20%;
height:20%;
z-index:1001;
text-align:center;
font-size:1.5em;
}
.loadingOver {
display:none;
position:absolute;
top:0;
left:0;
width:100%;
height:100%;
background-color:#f5f5f5;
opacity:0.5;
z-index:1000;
}
这里,多说一嘴:
关于input 的accept属性,这里只想读入Excel,所以
application/vnd.openxmlformats-officedocument.spreadsheetml.sheet, application/vnd.ms-excel
以上就是本文的全部内容,希望对大家的学习有所帮助。
本文原创发布php中文网,转载请注明出处,感谢您的尊重!