计算几何07_NURBS曲线与曲面

article/2025/8/21 9:36:25

在这里插入图片描述

B样条方法在表示与设计自由曲线曲面时展现出强大的威力，但在设计与表示初等曲线曲面时却遇到了麻烦。因为B样条曲线、及其特例的Bezier曲线都不能精确表示除抛物线以外的二次曲线弧，B样条曲面、及其特例的Bezier曲面都不能精确表示除抛物面以外的二次曲面，而只能给出近似表示。解决这一问题的途径是改进现有的B样条方法，在保留描述自由曲线曲面长处的同时，扩充其表示二次曲线弧与二次曲面的能力，这种方法就是有理B样条方法。

由于在曲线曲面描述中，B样条方法更多地以非均匀类型出现，而均匀、准均匀、分段Bezier三种类型又被看成是非均匀类型的特例，所以习惯上称之为非均匀有理B样条（Non-Uniform Rational B-Splines）方法，简称为NURBS方法。NURBS方法提出的主要理由是，寻找与描述自由曲线曲面的B样条方法相统一的，而又能精确表示二次曲线曲面的数学方法。非均匀B样条采用分段参数整数多项式，而NURBS方法采用分子分母分别是分段参数多项式函数与分段多项式的分式表示，是有理的。与有理Bezier方法一样，NURBS方法引入了权因子和分母。NURBS方法是在有理Bezier方法与非有理B样条方法的基础上发展起来的。

NURBS方法在CAD/CAM以及计算机图形学领域获得越来越广泛的应用，优点主要表现在以下几个方面：

  • 将初等曲线曲面与自由曲线曲面的表达方式统一起来。
  • 增加了权因子，有利于对曲线曲面形状的控制和修改。
  • 非有理B样条、有理与非有理Bezier方法是NURBS的特例。
  • 在比例、旋转、平移、错切以及平行和透视投影变换下是不变的。

在这里插入图片描述

一、NURBS曲线的定义及几何性质

在这里插入图片描述

1.1 有理分式表示

在这里插入图片描述
在这里插入图片描述
通常在实际应用中，端节点值分别取a = 0, b = 1。

1.2 有理基函数表示

在这里插入图片描述
则有，
在这里插入图片描述
式子中，Ri,k(t) ,i=0,1,…,n称为k次有理基函数。

1.3 齐次坐标表示

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

1.4 几何性质

在这里插入图片描述
在这里插入图片描述
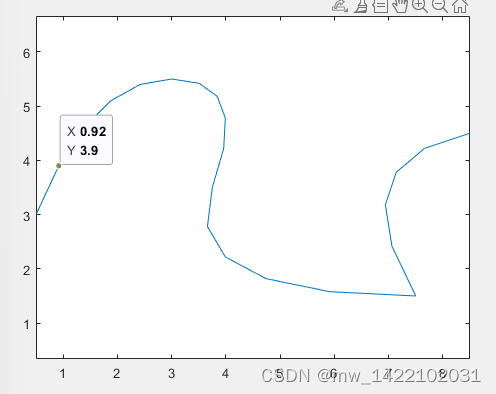
如下图，绘制的是3段三次NURBS曲线(n=5, k=3),虚线表示中间一段曲线。这段曲线包含在P1, P2, P3, P4构成的凸包内。图中这个凸包也用虚线围成。
在这里插入图片描述

在这里插入图片描述

二、权因子对NURBS曲线形状的影响

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

由NURBS曲线的定义可知，改变权因子、移动控制点或改变节点矢量，都将使NURBS曲线的形状发生变化。实践证明，采用改变节点矢量的方法修改NURBS曲线缺乏直观的几何意义，难以预料修改的结果。因此实际应用中，往往通过调整权因子或移动控制点来修改曲线形状。

在实际应用中，当需要修改曲线形状时，往往首先移动控制顶点。在曲线形状大致确定后，再根据需要在小范围内调整权因子，使曲线从整体到局部逐步达到要求。

三、NURBS曲线的形状修改

像非有理B样条曲线那样, NURBS曲线也可按所取节点向量划分成四种类型。
非有理B样条曲线的DeBoor算法求曲线上的点、插入节点、升阶等都可以推广到NURBS曲线。这些算法都应对高一维的带权控制顶点执行,然后,取其在0-1超平面上的投影即为所求。
采用NURBS方法可以将顺序相连的各种连续性的各种非有理与有理Bezier曲线、非有理和有理B样条曲线在更高层次上组合。
采用类似非有理B样条的组合方法,组合在一起,用一个统一方程表示,成为最具一般意义的NURBS曲线。

3.1 重新定位控制定点

在这里插入图片描述

3.2 反插节点

在这里插入图片描述

3.3 重新确定权因子

在这里插入图片描述

3.4 修改界定曲线部分

在这里插入图片描述

四、NURBS曲线代码实现

4.1 控制点初始化

	CP2 P[7];//控制点double W[7];//权因子double knot[11];//节点数组int n;//控制点数-1int k;//次数
CGeometricfiguretestView::CGeometricfiguretestView()
{// TODO: add construction code heren=6,k=3;P[0].x=-280;  P[0].y=30;//控制点P[1].x=-250;  P[1].y=180;P[2].x=0;     P[2].y=200;P[3].x=-100;  P[3].y=-100;P[4].x=150;   P[4].y=-100;P[5].x=130;   P[5].y=120;P[6].x=230;   P[6].y=150;W[0]=1.0,W[1]=2.0,W[2]=2.0,W[3]=2.0,W[4]=2.0,W[5]=2.0,W[6]=1.0;//权因子
}

4.2 绘制

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{CTestDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);if (!pDoc)return;// TODO: add draw code for native data hereCRect rect;//定义矩形GetClientRect(&rect);//获得客户区的大小pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点GetKnotVector();DrawNurbsCurve(pDC);DrawControlPolygon(pDC);
}void CGeometricfiguretestView::DrawNurbsCurve(CDC* pDC)//绘制NURBS曲线
{CPen NewPen,*pOldPen;NewPen.CreatePen(PS_SOLID,2,RGB(0,0,255));//曲线颜色pOldPen=pDC->SelectObject(&NewPen);	double tStep=0.01;for(double t=0.0;t<=1.0;t+=tStep){	CP2 p(0.0,0.0);double denominator=0.0;for(int i=0;i<=n;i++){	double BValue=GetBasisFunctionValue(t,i,k);			p+=P[i]*BValue*W[i];denominator+=BValue*W[i];}p/=denominator;//NURBS曲线定义if(0.0==t)pDC->MoveTo(ROUND(p.x),ROUND(p.y));elsepDC->LineTo(ROUND(p.x),ROUND(p.y));}  pDC->SelectObject(pOldPen);NewPen.DeleteObject();
}void CGeometricfiguretestView::DrawControlPolygon(CDC* pDC)//绘制控制多边形
{CPen NewPen,*pOldPen;NewPen.CreatePen(PS_SOLID,3,RGB(0,0,0));pOldPen=pDC->SelectObject(&NewPen);CBrush NewBrush,*pOldBrush;NewBrush.CreateSolidBrush(RGB(0,0,0));pOldBrush=pDC->SelectObject(&NewBrush);for(int i=0;i<=n;i++){if(0==i){pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);}else{pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);}}pDC->SelectObject(pOldBrush);pDC->SelectObject(pOldPen);
}void CGeometricfiguretestView::GetKnotVector()//哈德利-贾德方法获取节点值
{for(int i=0;i<=k;i++) //小于次数k的节点值为0knot[i]=0.0;for(int i=n+1;i<=n+k+1;i++)//大于n的节点值为1knot[i]=1.0;//计算n-k个内节点for(int i=k+1;i<=n;i++){double sum=0.0;for(int j=k+1;j<=i;j++)//公式（5-24）{ double numerator=0.0;//计算分子for(int loop=j-k;loop<=j-1;loop++){numerator+=sqrt((P[loop].x-P[loop-1].x)*(P[loop].x-P[loop-1].x)+(P[loop].y-P[loop-1].y)*(P[loop].y-P[loop-1].y));//计算两个点之间的距离}double denominator=0.0;//计算分母for(int loop1=k+1;loop1<=n+1;loop1++){for(int loop2=loop1-k;loop2<=loop1-1;loop2++){denominator+=sqrt((P[loop2].x-P[loop2-1].x)*(P[loop2].x-P[loop2-1].x)+(P[loop2].y-P[loop2-1].y)*(P[loop2].y-P[loop2-1].y));//计算两个点之间的距离}}	sum+=numerator/denominator;//计算节点值} knot[i]=sum;}
}double CGeometricfiguretestView::GetBasisFunctionValue(double t, int i, int k)//根据参数t值和次数k与节点矢量knot，计算第i个k次的B样条基函数
{double value1,value2,value;if(k==0){if(t>=knot[i] && t<knot[i+1])return 1.0;elsereturn 0.0;}if(k>0){if(t<knot[i]||t>knot[i+k+1])return 0.0;else{double coffcient1,coffcient2;//凸组合系数1，凸组合系数2double denominator=0.0;//分母denominator=knot[i+k]-knot[i];//递推公式第一项分母if(denominator==0.0)//约定0/0coffcient1=0.0;elsecoffcient1=(t-knot[i])/denominator;denominator=knot[i+k+1]-knot[i+1];//递推公式第二项分母if(0.0==denominator)//约定0/0coffcient2=0.0;elsecoffcient2=(knot[i+k+1]-t)/denominator;value1=coffcient1*GetBasisFunctionValue(t,i,k-1);//递推公式第一项的值value2=coffcient2*GetBasisFunctionValue(t,i+1,k-1);//递推公式第二项的值value=value1+value2;//基函数的值}}return value;
}

在这里插入图片描述

五、NURBS曲面

5.1 曲面定义三种表达方式

5.1.1 曲面有理分式表示

在这里插入图片描述

在这里插入图片描述

5.1.2 曲面有理基函数表示

在这里插入图片描述

5.1.3 曲面齐次坐标表示

在这里插入图片描述

5.2 曲面构造

在这里插入图片描述

5.3 曲面基函数性质

在这里插入图片描述

5.4 曲面性质

在这里插入图片描述

5.5 曲面权因子

在这里插入图片描述

5.6 曲面代码实现

5.6.1 曲面类构造

#pragma once
#include"P3.h"class CNurbsSurface
{
public:CNurbsSurface(void);~CNurbsSurface(void);void Initialize(CP3** pPoint, double** pWeight,int m,int p,int n,int q);//初始化void GetKnotVector(double* T,int nCount,int num,int order, BOOL bU);//获取节点矢量void DrawNurbsSurface(CDC* pDC);//绘制曲面double BasisFunctionValue(double u,int i,int k,double* T);//根据节点矢量T，计算基函数void DrawControlGrid(CDC* pDC);//绘制控制网格CP2 ObliqueProjection(CP3 Point3);//斜二测投影
public:int m,p;//m为u向的顶点数减1，p为次数    int n,q;//n为v向的顶点数减1，q为次数CP3** P;//三维控制点double** W;//权因子double** U;//V为v向节点矢量数组double** V;//U为u向节点矢量数组	
};

#include "StdAfx.h"
#include "NurbsSurface.h"
#include<math.h>
#define ROUND(d) int(d+0.5)
const double PI = 3.1415926;CNurbsSurface::CNurbsSurface(void)
{P=NULL;U=NULL;V=NULL;
}CNurbsSurface::~CNurbsSurface(void)
{if(NULL!=P){for(int i=0;i<n+1;i++){delete []P[i];P[i]=NULL;}delete []P;P=NULL;}if(NULL!=W){for(int i=0;i<n+1;i++){delete []W[i];W[i]=NULL;}delete []W;W = NULL;}if(NULL!=U){for(int i=0;i<n+1;i++){delete []U[i];U[i] = NULL;}delete []U;U=NULL;}if(NULL!=V){for(int i=0;i<m+1;i++){delete []V[i];V[i]=NULL;}delete []V;V=NULL;}
}void CNurbsSurface::Initialize(CP3** pPoint, double** pWeight,int m,int p,int n,int q)//曲面参数初始化
{P=new CP3* [n+1];//建立控制顶点的动态二维数组for(int i=0;i<n+1;i++)P[i]=new CP3[m+1];W=new double*[n+1];//建立权因子的动态二维数组for(int i=0;i<n+1;i++)W[i]=new double[m+1];for(int i=0;i<n+1;i++)//二维控制顶点数组初始化for(int j=0;j<m+1;j++)P[i][j]=pPoint[i][j];for(int i=0;i<n+1;i++)//二维权因子数组初始化for(int j=0;j<m+1;j++)W[i][j]=pWeight[i][j];this->m=m,this->p=p;this->n=n,this->q=q;U=new double* [n+1];//建立u向节点矢量动态数组for(int i=0;i<n+1;i++)U[i]=new double[m+p+2];	V=new double* [m+1];//建立v向节点矢量动态数组for(int i=0;i<m+1;i++)V[i]=new double[n+q+2];
}void CNurbsSurface::DrawNurbsSurface(CDC* pDC)//绘制曲面
{for(int i=0;i<n+1;i++)GetKnotVector(U[i],i,m,p, TRUE);//获取节点矢量Ufor(int i=0;i<m+1;i++)GetKnotVector(V[i],i,n,q, FALSE);//获取节点矢量V	CPen NewPen(PS_SOLID,1,RGB(0,0,255));//曲线颜色CPen* pOldPen=pDC->SelectObject(&NewPen);double Step=0.1;//步长for(double u=0.0;u<=1.0;u+=Step){for(double v=0.0;v<=1.0;v+=Step){CP3 point(0,0,0);double weight=0.0;for(int i=0;i<n+1;i++){for(int j=0;j<m+1;j++){double BValueU=BasisFunctionValue(u,j,p,U[i]);double BValueV=BasisFunctionValue(v,i,q,V[j]);point+=P[i][j]*W[i][j]*BValueU*BValueV;weight+=W[i][j]*BValueU*BValueV;}}point/=weight;CP2 Point2=ObliqueProjection(point);//斜投影if (v==0.0)pDC->MoveTo(ROUND(Point2.x),ROUND(Point2.y));elsepDC->LineTo(ROUND(Point2.x),ROUND(Point2.y));}}for(double v=0.0;v<=1.0;v+=Step){for(double u=0.0;u<=1.0;u+=Step){CP3 point(0,0,0);double weight=0.0;for(int i=0;i<n+1;i++){for(int j=0;j<m+1;j++){double BValueU=BasisFunctionValue(u,j,p,U[i]);double BValueV=BasisFunctionValue(v,i,q,V[j]);point+=P[i][j]*W[i][j]*BValueU*BValueV;weight+=W[i][j]*BValueU*BValueV;}}point/=weight;CP2 Point2=ObliqueProjection(point);//斜投影if (u==0.0)pDC->MoveTo(ROUND(Point2.x),ROUND(Point2.y));elsepDC->LineTo(ROUND(Point2.x),ROUND(Point2.y));}}pDC->SelectObject(pOldPen);NewPen.DeleteObject();
}void CNurbsSurface::DrawControlGrid(CDC* pDC)//绘制控制网格
{CP2** P2=new CP2*[n+1];for(int i=0;i<n+1;i++)P2[i]=new CP2[m+1];for(int i=0;i<n+1;i++)for(int j=0;j<m+1;j++)P2[i][j]=ObliqueProjection(P[i][j]);CPen NewPen,*pOldPen;NewPen.CreatePen(PS_SOLID,1,RGB(255,255,0));pOldPen=pDC->SelectObject(&NewPen);CBrush NewBrush(RGB(0,0,0));CBrush* pOldBrush=pDC->SelectObject(&NewBrush);for(int i=0;i<n+1;i++)//绘制v向控制网格{pDC->MoveTo(ROUND(P2[i][0].x),ROUND(P2[i][0].y));pDC->Ellipse(ROUND(P2[i][0].x)-5,ROUND(P2[i][0].y)-5,ROUND(P2[i][0].x)+5,ROUND(P2[i][0].y)+5);for(int j=1;j<m+1;j++){pDC->LineTo(ROUND(P2[i][j].x),ROUND(P2[i][j].y));pDC->Ellipse(ROUND(P2[i][j].x)-5,ROUND(P2[i][j].y)-5,ROUND(P2[i][j].x)+5,ROUND(P2[i][j].y)+5);}}for(int j=0;j<m+1;j++)//绘制u向控制网格{pDC->MoveTo(ROUND(P2[0][j].x),ROUND(P2[0][j].y));for(int i=1;i<n+1;i++)pDC->LineTo(ROUND(P2[i][j].x),ROUND(P2[i][j].y));}pDC->SelectObject(pOldPen);NewPen.DeleteObject();if(NULL!=P2){for(int i=0;i<n+1;i++){delete []P2[i];P2[i]=NULL;}delete []P2;P2=NULL;}pDC->SelectObject(pOldPen);pDC->SelectObject(pOldBrush);	
}void CNurbsSurface::GetKnotVector(double* T,int nCount,int num,int order, BOOL bU)//哈德利-贾德算法获取节点矢量数组
{for(int i=0;i<=order;i++) //小于等于曲线次数order的节点值为0T[i]=0.0;for(int i=num+1;i<=num+order+1;i++)//大于顶点数减1（n）的节点值为1T[i]=1.0;//计算num-order个内节点for(int i=order+1;i<=num;i++)  {double sum=0.0;for(int j=order+1;j<=i;j++){ double numerator=0.0;//计算分子for(int loop=j-order;loop<=j-1;loop++){if(bU)//选择计算节点矢量U还是计算节点矢量Vnumerator+=(P[nCount][loop].x-P[nCount][loop-1].x)*(P[nCount][loop].x-P[nCount][loop-1].x)+(P[nCount][loop].y-P[nCount][loop-1].y)*(P[nCount][loop].y-P[nCount][loop-1].y);elsenumerator+=(P[loop][nCount].x-P[loop-1][nCount].x)*(P[loop][nCount].x-P[loop-1][nCount].x)+(P[loop][nCount].y-P[loop-1][nCount].y)*(P[loop][nCount].y-P[loop-1][nCount].y);}double denominator=0.0;//计算分母for(int loop1=order+1;loop1<=num+1;loop1++){for(int loop2=loop1-order;loop2<=loop1-1;loop2++){if(bU)denominator+=(P[nCount][loop2].x-P[nCount][loop2-1].x)*(P[nCount][loop2].x-P[nCount][loop2-1].x)+(P[nCount][loop2].y-P[nCount][loop2-1].y)*(P[nCount][loop2].y-P[nCount][loop2-1].y);elsedenominator+=(P[loop2][nCount].x-P[loop2-1][nCount].x)*(P[loop2][nCount].x-P[loop2-1][nCount].x)+(P[loop2][nCount].y-P[loop2-1][nCount].y)*(P[loop2][nCount].y-P[loop2-1][nCount].y);}} sum+=numerator/denominator;			}T[i]=sum;}
}double CNurbsSurface::BasisFunctionValue(double t,int i,int order,double* T)//计算B样条基函数
{double value1,value2,value;if(order==0){if(t>=T[i] && t<T[i+1])return 1.0;elsereturn 0.0;}if(order>0){if(t<T[i]||t>T[i+order+1])return 0.0;else{double coffcient1,coffcient2;//凸组合系数1，凸组合系数2double denominator=0.0;//分母denominator=T[i+order]-T[i];//递推公式第一项分母if(denominator==0.0)//约定0/0coffcient1=0.0;elsecoffcient1=(t-T[i])/denominator;denominator=T[i+order+1]-T[i+1];//递推公式第二项分母if(0.0==denominator)//约定0/0coffcient2=0.0;elsecoffcient2=(T[i+order+1]-t)/denominator;value1=coffcient1*BasisFunctionValue(t,i,order-1,T);//递推公式第一项的值value2=coffcient2*BasisFunctionValue(t,i+1,order-1,T);//递推公式第二项的值value=value1+value2;//基函数的值}}return value;
}CP2 CNurbsSurface::ObliqueProjection(CP3 Point3)//斜二测投影
{CP2 Point2;Point2.x=Point3.x-Point3.z*sqrt(2.0)/2.0;Point2.y=Point3.y-Point3.z*sqrt(2.0)/2.0;return Point2;
}

5.6.2 曲面数据初始化

	CP3** P3;//二维控制网格double** W;//权值int m,n;//u向和v向的控制点数-1int p,q;//u向和v向的次数CNurbsSurface NurbsSurface;//NURBS曲面对象CGeometricfiguretestView::CGeometricfiguretestView()
{// TODO: add construction code herem=4,p=3;//u向顶点数 5 个，曲线次数为 3 次n=4,q=3;//v向顶点数 5 个，曲线次数为 3 次P3=new CP3*[n+1];		//建立控制顶点的动态二维数组for(int i=0;i<n+1;i++)P3[i]=new CP3[m+1];W=new double*[n+1];		//建立权值的动态二维数组for(int i=0;i<n+1;i++)W[i]=new double[m+1];for(int i=0;i <n + 1;i++)for(int j=0;j<m+1;j++)W[i][j]=1;P3[0][0].x=82;  P3[0][0].y=-100;P3[0][0].z=200;P3[0][1].x=-14; P3[0][1].y=65;  P3[0][1].z=150;P3[0][2].x=-146;P3[0][2].y=94;  P3[0][2].z=50;P3[0][3].x=-254;P3[0][3].y=80;  P3[0][3].z=0;P3[0][4].x=-301;P3[0][4].y=40;  P3[0][4].z=50;P3[1][0].x=147; P3[1][0].y=68; P3[1][0].z=150;P3[1][1].x=52;  P3[1][1].y=117;P3[1][1].z=100;P3[1][2].x=-68; P3[1][2].y=146;P3[1][2].z=50;P3[1][3].x=-173;P3[1][3].y=135;P3[1][3].z=-10;P3[1][4].x=-238;P3[1][4].y=131;P3[1][4].z=-10;P3[2][0].x=227; P3[2][0].y=132;P3[2][0].z=140;P3[2][1].x=125; P3[2][1].y=154;P3[2][1].z=80;P3[2][2].x=0;   P3[2][2].y=178;P3[2][2].z=30;P3[2][3].x=-109;P3[2][3].y=166;P3[2][3].z=-50;P3[2][4].x=-164;P3[2][4].y=174;P3[2][4].z=0;P3[3][0].x=337; P3[3][0].y=131;P3[3][0].z=150;P3[3][1].x=205; P3[3][1].y=173;P3[3][1].z=50;P3[3][2].x=75;  P3[3][2].y=203;P3[3][2].z=0;P3[3][3].x=-51; P3[3][3].y=188;P3[3][3].z=-70;P3[3][4].x=-116;P3[3][4].y=178;P3[3][4].z=-100; P3[4][0].x=390; P3[4][0].y=50; P3[4][0].z=150;P3[4][1].x=288; P3[4][1].y=162;P3[4][1].z=50;P3[4][2].x=172; P3[4][2].y=208;P3[4][2].z=0;P3[4][3].x=48;  P3[4][3].y=201;P3[4][3].z=-70; P3[4][4].x=-8;  P3[4][4].y=200;P3[4][4].z=50;NurbsSurface.Initialize(P3,W,n,q,m,p);
}

5.6.3 调用绘制

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{CTestDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);if (!pDoc)return;// TODO: add draw code for native data hereCRect rect;//定义矩形GetClientRect(&rect);//获得客户区的大小pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点rect.OffsetRect(-rect.Width()/2,-rect.Height()/2);DrawGraph(pDC);//绘制图形
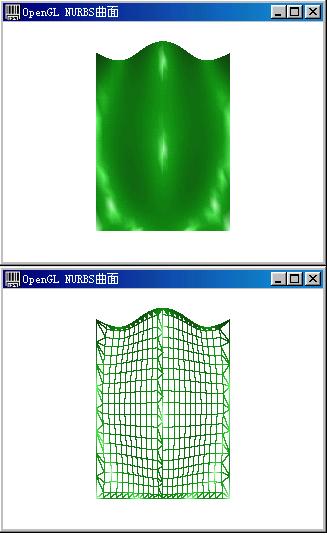
}void CGeometricfiguretestView::DrawGraph(CDC* pDC)//绘制NURBS曲面
{NurbsSurface.DrawNurbsSurface(pDC);NurbsSurface.DrawControlGrid(pDC);
}

在这里插入图片描述
你也可以改变权重查看效果
在这里插入图片描述

六、总结–三次参数曲线

6.1 性质比较

在这里插入图片描述

6.2 曲线间转换

在这里插入图片描述


http://chatgpt.dhexx.cn/article/pVWq4uvG.shtml

相关文章

利用NURBS曲线进行点云曲面拟合算法

利用NURBS曲线进行点云曲面拟合算法

文章目录 介绍NURBS曲线C实现思路代码实现读取点云数据对点云进行预处理创建曲面模型将曲面模型转换为NURBS曲面 完整代码opennurbs.h说明vs2019安装OpenNURBS库编译OpenNURBS库 介绍 点云拟合曲面算法是将点云数据拟合成一个二次或高次曲面模型的算法。这种算法主要用于三维模…
阅读更多...
离散数据点NURBS曲线拟合算法

离散数据点NURBS曲线拟合算法

问题描述&#xff1a;对于离散数据点集来说&#xff0c;其主要特征点一般可以描述原始曲线轨迹的基本形状。对于大量的离散数据点来说&#xff0c;提取主要的特征点后在进行曲线拟合&#xff0c;这样可以降低计算次数&#xff0c;极高拟合效率。 可以描述原始曲线几何形状的 特…
阅读更多...
Nurbs建模

Nurbs建模

多边形建模和Nurbs建模 Nurbs始终有四个侧面&#xff0c;由有理多项式方程创立的曲线&#xff0c;由控制点定义的曲线。 Nurbs曲线是由一系列多项式构成的&#xff1a;axb0,ax^2bxc0… 能够将任何平面转换为Nurbs NURBS能买构建几乎所有的形状
阅读更多...
matlab中Nurbs库的简单使用

matlab中Nurbs库的简单使用

文章目录 前言一、简单例子二、复杂一点的NUrbs曲面nrbeval函数 前言 只是为方便学习&#xff0c;不做其他用途&#xff0c;记录matlab中Nurbs的使用&#xff0c;好像记得是添加的matlab中的一个Nurbs库来着。前一段使用&#xff0c;现在不记得了&#xff0c;使用这个程序得先安…
阅读更多...
NURBS

NURBS

非均匀有理样条NURBS( Non-Uniform Rational B-Splines ) 是近年来发展迅速&#xff0c;应用广泛的一种表示曲线曲面造型技术。它能够精确地表示二次规则曲线曲面&#xff0c;从而能用统一的数学形式表示规则曲面与自由曲面&#xff0c;具有可影响曲线曲面形状的权因子&#xf…
阅读更多...
【Matlab-NURBS工具箱简要教程及实例 】

【Matlab-NURBS工具箱简要教程及实例 】

Matlab-NURBS工具箱使用教程 添加NURBS工具箱 在附加功能里添加NURBS工具箱 安装完成后可以在’函数’处查看API&#xff0c;也打开文件夹查看。 强烈推荐同步安装gnurbs工具&#xff0c;它完全代替nrbplot展示曲面&#xff0c;且允许用户进行节点拖拽等操作。 NURBS 结…
阅读更多...
Nurbs曲线详解

Nurbs曲线详解

NURBS&#xff08;Non Uniform Rational B-spline&#xff09;曲线通常称为非均匀有理B样条曲线&#xff0c;其数学定义如下&#xff1a; 基函数由递推公式定义&#xff1a; 非均匀&#xff1a;指节点向量的值与间距可以为任意值。这样我们可以在不同区间上得到不同的混合…
阅读更多...
NURBS曲面结构及生成原理、修改方法

NURBS曲面结构及生成原理、修改方法

NURBS全称是Non-Uniform Rational B-Splines中文叫做非均匀有理B样条曲线&#xff0c;Rhinoceros中的模型曲线便是通过NRUBS曲线进行描述&#xff0c;曲面则是通过U和V两个方向的曲线集合来得到&#xff0c;如图&#xff1a; Rhino如何生产曲面原理 由上图我们发现就像织布一样…
阅读更多...
MySQL数据库增量备份及恢复方案

MySQL数据库增量备份及恢复方案

MySQL数据库增量备份及恢复方案 u 前言 操作系统崩溃、电源故障、文件系统崩溃和硬件故障等异常状况都可能导致我们正在使用的数据库出现故障而产生数据库中数据不一致的情况。为了保证数据库使用安全&#xff0c;必须定期备份数据库&#xff1b;数据库备份可以分为&#xff1…
阅读更多...
差异增量备份和累积增量备份区别（有图）

差异增量备份和累积增量备份区别（有图）

所谓增量备份&#xff0c;顾名思义即是每次备份仅操作那些发生了"变化"的数据块。RMAN中增量备份有两种&#xff1a;Differential 方式和Cumulative方式。 1、差异增量备份Differential 说起Differential&#xff0c;相当有意思&#xff0c;大家可以这样理解。有一…
阅读更多...
数据库的备份与恢复（完全备份，增量备份）

数据库的备份与恢复（完全备份，增量备份）

目录 1. 数据库备份的分类1.1 从物理与逻辑的角度&#xff0c;备份可分为1.2 从数据库的备份策略角度&#xff0c;备份可分为 2. 常见的备份方法3. MySQL完全备份与分类3.1 完全备份概述3.2 备份方式3.2.1 物理冷备份及恢复3.2.2 使用专用备份工具 mysqldump3.2.2.1 备份库3.2.…
阅读更多...
图解完全备份，增量备份，差异备份

图解完全备份，增量备份，差异备份

因为网上说的全部都是copy的&#xff0c;所以自己去理解了一下然后整理了一下。 完全备份 完成备份我相信大家都理解&#xff0c;就是一下子备份所有的内容。 增量备份 如上图所示&#xff0c;比如一家公司&#xff0c;周一这家公司进行完全备份&#xff0c;然后周二备份周一…
阅读更多...
MySQL 增量备份与恢复

MySQL 增量备份与恢复

目录 引言一、MySQL 增量备份1. 增量备份特点2. 示例 二、MySQL 增量恢复1. 增量恢复的场景2. 丢失完全备份之后更改的数据的恢复3. 完全备份之后丢失所有数据4. 基于时间点与位置的恢复4.1 基于时间点的恢复4.2 基于位置的恢复 5. 指定企业备份策略的思路 总结 引言 完全备份…
阅读更多...
增量备份恢复

增量备份恢复

** 增量备份恢复案例 **1、配置mysql&#xff0c;设置日志文件 [rootlocalhost bak]# vim /etc/my.cnf 添加&#xff1a; log-binmysql-bin2、重启mysqld服务 systemctl restart mysqld查看日志文件&#xff1a; mysqlbinlog /usr/local/mysql/data/mysql-bin.0000013、创…
阅读更多...
mysql实现增量备份

mysql实现增量备份

有点要注意 如果你误删了表 想通过这个恢复 必须恢复日志里面有创建表的日志 不然的话是无法回复的 就是必须是从你开始创建表的时候就已经记录日志了 恢复到哪个位置 就按照哪个位置来计算 mysql 5.0不支持增量备份 增量备份定义 mysql数据库会以二进制形式 自动把用户对my…
阅读更多...
什么是全量备份,增量备份,差异备份?

什么是全量备份,增量备份,差异备份?

背景 今天我司服务器工程大牛看我在备份数据,冷不丁提到了差异备份;但是才疏学浅的我却不知何为差异备份,故而以此为引,开始了对全量备份,增量备份,差异备份这三者的研习;经过一番寻觅,最终找到了他们.呵呵 希望大家有所受益! 问题 1. 什么是全量备份&#xff1f; 2. 什么是增量…
阅读更多...
MySQL完全备份和增量备份

MySQL完全备份和增量备份

MySQL日治管理、数据库备份与恢复 备份的主要目的是灾难恢复&#xff0c;备份还可以测试应用、回滚数据修改、查询历史数据、审计等。而备份、恢复中&#xff0c;日志起到了很重要的作用 一、日志 MySQL的日志默认保存位置为 /usr/local/mysql/data 1.日志类型与作用 ①re…
阅读更多...
MySQL 数据库备份（增量备份与恢复）

MySQL 数据库备份（增量备份与恢复）

目录 一、MySQL 增量备份 1.增量备份的概念 1.1 为什么使用增量备份 1.2 增量备份的特点 2.增量备份示例 二、MySQL 增量恢复 1.增量恢复的场景 2.丢失完全备份之后更改的数据的恢复步骤 3.完全备份之后丢失所有数据的恢复步骤 4. 基于时间点与位置的恢复 4.1 基于时间…
阅读更多...
mysql数据的备份与恢复

mysql数据的备份与恢复

mysql数据的备份与恢复 日志的类型与作用&#xff1a;开启日志方式查看日志是否开启 数据备份的重要性&#xff1a;备份类型&#xff1a;如何选择逻辑备份策略或频率&#xff1f;常见的备份方法&#xff1a;MysQL完全备份优缺点&#xff1a;数据库完全备份分类&#xff1a; 实验…
阅读更多...
完全备份 、差异备份、增量备份的区别和特点

完全备份 、差异备份、增量备份的区别和特点

数据备份的方式有完全备份、差异备份以及增量备份&#xff0c;那么这三种备份方式有什么区别&#xff0c;在具体应用中又该如何选择呢&#xff1f;本文就这些问题作以介绍。 一、备份方式简介 1、完全备份&#xff08;Full Backup&#xff09; 备份全部选中的文件夹&#xf…
阅读更多...
推荐文章

Copyright @ 2022~2023