最不能理解的一点，一讨论软件的曲面，曲线功能，最后就变成曲线、曲面的数学原理的讨论了，但是里面也没数学好的，讨论的结果可想而知。

我不是数学家，我不懂这么复杂的方程，只要好用就行了。

在CAD中，设计师需要设计出各种各样的曲线；数学中，曲线是通过各种各样的方程表示的，比如一条通过点A(0,0)、B(1,1)的直线可以表示为：

y=x

或者用参数方程表示：

            P(u) = (1-u)A+tB

再比如一个通过原点(1,2)、半径为2的圆可以表示为：

            (x-1)^2 + (y-2)^2 = 4

或者用参数方程表示：

            x = 2cos(u)+1

            y = 2sin(u)+2

上面举例的是两种很简单的曲线，对于更复杂的曲线可以用更复杂的方程来表示（比如用高次多项式）；

如果我们的设计师是一位数学家就好了，他可以根据自己的需要，设计出一个复杂的方程来表示自己想要的一条优美的曲线，但是事与愿违，设计师们往往想通过一种直观的方式来设计曲线，而不是利用方程。

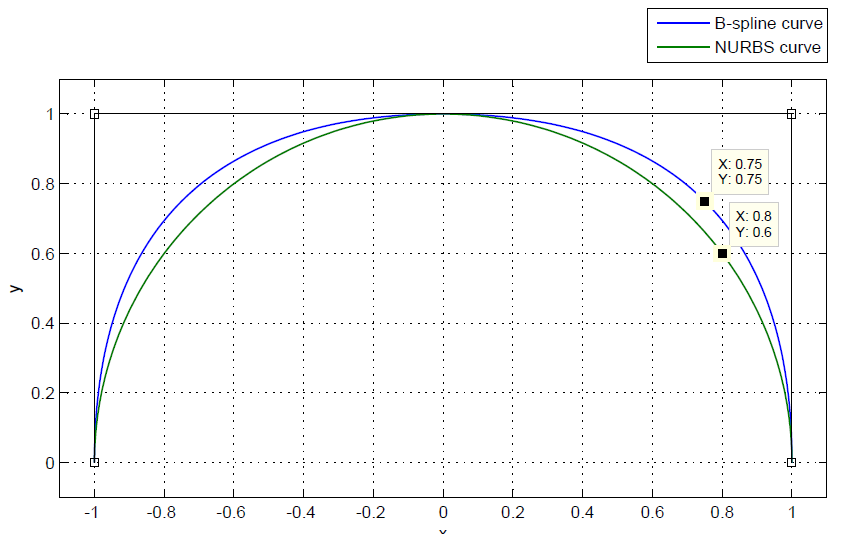
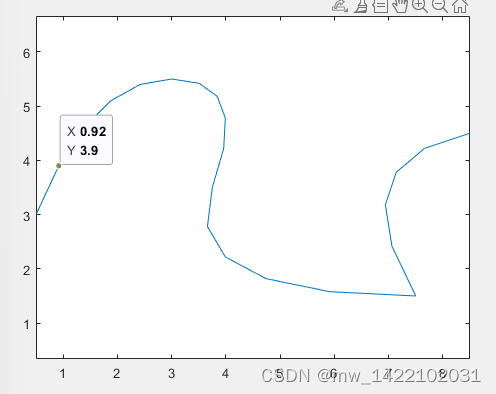
因此，诸位科学家和工程师设计出了Bezier曲线、B样条和NURBS，下面是一个有四个控制点的Bezier曲线：

 

可以通过改变一个控制点的位置来改变曲线的形状，比如将上图曲线中左边第二个控制点往上移，就可以得到下面的曲线:

 

可以看到，这种曲线生成方式比较直观和灵活，我只需要放置控制点，然后调整控制点的位置来得到想要的曲线，这就避免了和复杂的数学方程打交道，岂不快哉？

Bezier曲线、B样条和NURBS都是根据控制点来生成曲线的，那么他们有什么区别了？简单来说，就是:

§  Bezier曲线中的每个控制点都会影响整个曲线的形状，而B样条中的控制点只会影响整个曲线的一部分，显然B样条提供了更多的灵活性；

§  Bezier和B样条都是多项式参数曲线，不能表示一些基本的曲线，比如圆，所以引入了NURBS，即非均匀有理B样条来解决这个问题；

 

Bezier曲线只是B样条的一个特例而已，而B样条又是NURBS的一个特例，它们的关系可以图示为：

 

 

B样条克服了Bezier曲线的一些缺点，Bezier曲线的每个控制点对整条曲线都有影响，也就是说，改变一个控制点的位置，整条曲线的形状都会发生变化，而B样条中的每个控制点只会影响曲线的一段参数范围，从而实现了局部修改；

转载地址：http://blog.sina.com.cn/s/blog_684860810102dxmt.html