前言

采用matlab实现NURBS逼近曲线的拟合，利用app designer实现拟合的界面，辅助验证各种方法。文中主要是自己实现写的算法，可以得到逼近曲线，以及进行曲线性能的简单评判。

文中只简单介绍了一些理论，也是个人的一下理解，或许有误。详细理论看施法中《计算机辅助几何设计与非均匀有理B样条》一书，极其详细，好多论文里面提到的方法及背景，发展历史都能在里面找到。

在哔哩哔哩上传了分开的内容，用于记录。全部内容总结在本文：哔哩哔哩专栏地址

实现的效果可以参考哔哩哔哩内视频：视频地址

全部的代码内容：代码压缩文件有问题联系。

再次说明一下，使用的是逼近曲线，不是插值曲线，没有涉及切矢计算，采用最小二乘方法。

一、数据点参数化

1.1原因

采用参数多项式构造插值函数，顺序通过n+1个点不超过n次的参数多项式曲线可能有无数条。欲使唯一确定一条插值曲线就需要先对数据点赋予参数化，使其形成严格递增序列： u0＜u1……＜um 。(我也没太明白，咋就有无数条了，传入数据点不就有数据顺序了嘛)

1.2方法

数据点参数化方法主要有均匀参数化、积累弦长、向心、福利参数化方法。只实现了前三个，最后一个没找到资料。

均匀参数化法使节点在参数轴上等距分布，在相邻弦长差距大的情况下，得到的曲线会出现弦长长段曲线扁平，弦长短段曲线凸起的现象，甚至出现尖点或自交点。这些问题其他方法也有。

积累弦长引入弦长信息，得到改善；向心引入弦长折拐信息，改善；福利参数方法引入修正系数，使折拐不是简单的稳定数值。(仅个人理解) 三种方法比对图。

1.3代码(封装到类)

%数据参数化
classdef Parametrizationpropertiesp %数据endmethodsfunction obj = Parametrization(a)obj.p = a.data;endfunction dataPara = USM(obj)data = obj.p;n = size(data,1);dataPara = zeros(1,n);for i = 1:ndataPara(i) = (i-1)/(n-1);endendfunction dataPara = CLM(obj)data = obj.p;n = size(data,1);dataPara = zeros(1,n);L = GetTwoPointsDis(data, 1);for i = 2:(n-1)dataPara(i) = sum(L(1:i-1))/sum(L(:));enddataPara(n) = 1;endfunction dataPara = CM(obj)data = obj.p;n = size(data,1);dataPara = zeros(1,n);L = GetTwoPointsDis(data, 1/2);for i = 2:(n-1)dataPara(i) = sum(L(1:i-1))/sum(L(:));enddataPara(n) = 1;endend
end
function Dis = GetTwoPointsDis(data, p)%data控制点 n行2列   q次数(1,弦长 1/2向心)n = size(data, 1);Dis = zeros(1,n-1);for i = 1:n-1A = norm(data(i,:) - data(i+1,:));Dis(i) = A^(p);end
end

二、节点矢量计算

2.1方法

写了AVG+KTP的方法，和UAVG方法。这两个公式好找，好实现；特征点、支配点、遗传算法这些没找到公式。遗传算法迷宫时候学过概念，没掌握精髓。

2.2代码

%计算节点矢量
classdef GetKnotspropertiesdatadataParakctrPnumsendmethodsfunction obj = GetKnots(a)obj.data = a.data;%数据点 得到个数obj.dataPara = a.dataPara;%数据点参数obj.k = a.k;%次数obj.ctrPnums = a.ctrPnums;%控制点个数endfunction knots = AVG_KTP(obj)m = size(obj.data,1);n = obj.ctrPnums;u = obj.dataPara;knots = zeros(1,n+obj.k+1);knots(n+1: n+obj.k+1) = 1;if m == nfor j = 1:(n-obj.k-1)knots(obj.k+j+1) = sum(u(j+1:j+obj.k)) / obj.k;endendif m>nc = m / (n - obj.k);for j = 1:n-obj.k-1i = floor(j * c);a = j*c - i;knots(obj.k+j+1) = (1-a)* u(i) + a * u(i+1);endendendfunction knots = UAVG(obj)m = size(obj.data,1);n = obj.ctrPnums;u = obj.dataPara;knots = zeros(1,n+obj.k+1);knots(n+1: n+obj.k+1) = 1;for j = 1:(n-obj.k-1)knots(j+obj.k+1) = sum(u(j+1:j+obj.k+m-n))/(obj.k+m-n);endendend
end

三、最小二乘反算控制点

采用的是逼近曲线，用的最小二乘法，切矢这些不包含在内,原理就是采取曲线偏差的一个函数，令其偏导为0。得到反算的公式。

输入是一个结构体。

function ctrP = InvCtrP(InputsStruct)data = InputsStruct.data;dataPara = InputsStruct.dataPara;knots = InputsStruct.knots;k = InputsStruct.k;ctrPnums = InputsStruct.ctrPnums;m = size(data,1);%计算r矩阵r = zeros(ctrPnums-2,2);for i = 2:(m-1)r(i-1,:) = data(i,:)-data(1,:).*GetBasisFcn(dataPara(i),knots,0,k)...-data(m,:).*GetBasisFcn(dataPara(i),knots,ctrPnums-1,k);end%计算N矩阵N = zeros(m-2,ctrPnums-2);for j = 2:(m-1)x = zeros(1,ctrPnums-2);for i = 2:(ctrPnums-1)x(i-1) = GetBasisFcn(dataPara(j),knots,i-1,k);endN(j-1,:) = x;endR = N'*r;ctrP = [data(1,:);(N'*N)\R; data(m,:)];
end

其中主要是基函数的实现，一开始不知道什么问题老是在一点处变为2倍，后面一直没搞这个，再次运行又没事了。基函数实现在下一篇，不知道为什么基函数插入代码显示不出来。。。

四、基函数实现

不显示代码可能是因为&&这个

%%%%%%%%%%%这里的代码是

if (x>=knots(i+1)) && (x<knots(i+2))

没有这一句，matlab里面会显示红色提示的。

下面注释的代码是最开始采取的基函数计算方式

输入自变量，节点、第几个、k次数；注释内容是第二种实现方式，本质一样。

function res = GetBasisFcn(x,knots,i,k)if k == 0%%%%%%%%%%%%%%%%%%%%%%%%%%%%res = 1;elseres = 0;endelseA = GetBasisFcn(x, knots, i, k-1);B = GetBasisFcn(x, knots, i+1, k-1);if A == 0w1 = 0;  %防止迭代过程中 出现分母为0情况elsew1 = (x - knots(i+1)) / (knots(i+k+1) - knots(i+1));endif B == 0w2 = 0;elsew2 = (knots(i+k+2) - x) / (knots(i+k+2) - knots(i+2));endres = w1 * A + w2 * B;end
end
% function res = GetBasisFcn(x,knots,fre,k)
%     N = [];
%     for i = 1:(size(knots,2)-1)
%         %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%             N(i,1) = 1;
%         else
%             N(i,1) = 0;
%         end
%     end
%     for i = 1:(size(knots,2)-1)
%         for j = 1:(size(knots,2)-i-1)
%             if N(j,i) == 0
%                 w1 = 0;
%             else
%                 w1 = (x-knots(j)) / (knots(i+j) - knots(j));
%             end
%             if N(j+1,i) == 0
%                 w2 = 0;
%             else
%                 w2 = (knots(i+j+1)-x) / (knots(i+j+1) - knots(j+1));
%             end
%             N(j,i+1) = w1*N(j,i) + w2*N(j+1,i);
%         end
%     end
%
%     res = N(fre+1,k+1);
% end

五、豪斯多夫距离

在得到拟合后的曲线后，需要评估效果。

目标函数采取豪斯多夫距离评定偏差，这个好理解，理论很多。

曲线光顺性采取的离散曲率，这个没细看，简单实现一下。

返回偏差、以及在两组数据中的序号


%豪斯多夫距离 单向
% function [dis,number] = Hausdorff(p,Q)
%     [pToQ_dis,number] = Hausdorff_pToQ(p,Q);
%     QTop_dis = Hausdorff_pToQ(Q,p); 
%     
%     dis = max(pToQ_dis, QTop_dis);
% end
function [dis, numberp, numberQ] = Hausdorff(p,Q)m = size(p, 1);n = size(Q, 1);   pAllToQ_MaxDis = 0;for i = 1:mpEach = p(i,:);pEachToQ_MinDis = 10;for j = 1:nQEach = Q(j,:);if pEachToQ_MinDis>norm(pEach-QEach)pEachToQ_MinDis = norm(pEach-QEach);x = j;endendif pAllToQ_MaxDis<pEachToQ_MinDispAllToQ_MaxDis = pEachToQ_MinDis;numberp = i;numberQ = x;end  enddis = pAllToQ_MaxDis;
end

六、离散曲率

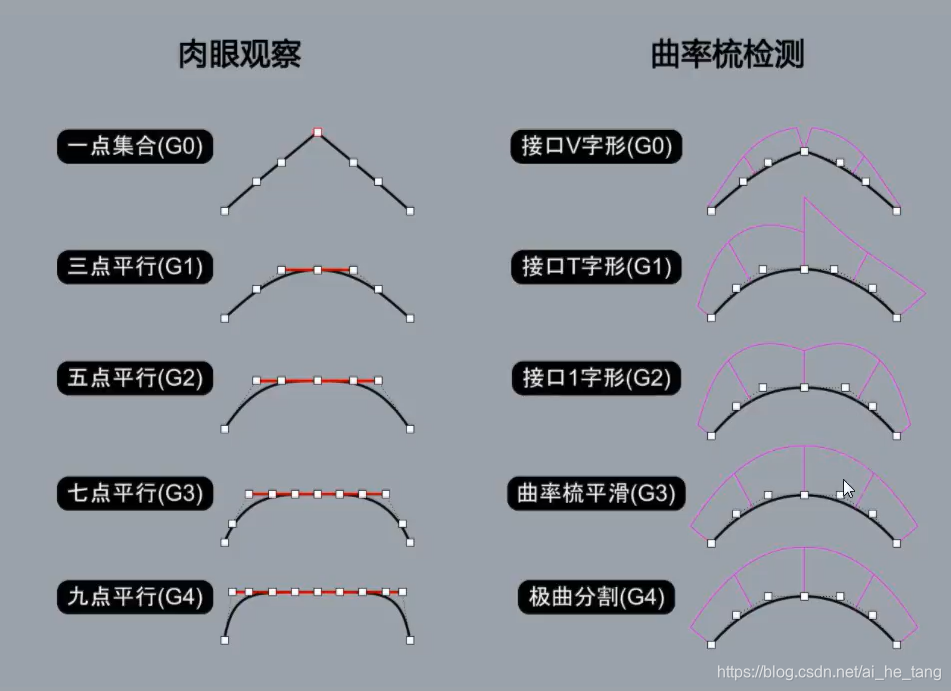
曲线光顺性方法也有好多。基于曲率、基于能量、二者结合等等。

采取基于曲率，需要计算导数，但是计算导数前后两个点挺头疼的。

在一篇论文里找到一种方法。具体忘叫啥了，好像是第二类离散曲率。进行了转换

function C = Curvature(data)%计算离散曲率图%增加-1 n+1点 变为Qdata_rows = size(data,1);Q = zeros(data_rows+2, 2);Q(1,:) = 2*data(1,:) - data(2,:);Q(2:data_rows+1,:) = data;Q(data_rows+2,:) = 2*data(data_rows,:) - data(data_rows-1,:);%迭代计算C = zeros(1,data_rows);for i = 2:data_rows+1Li = norm(Q(i,:) - Q(i-1,:));Li_1 = norm(Q(i+1,:) - Q(i,:));Mi = norm(Q(i+1,:) - Q(i-1,:));%三角形 有向面积D = ones(3);for j = 1:3D(j,1:2) = Q(i+j-2,:);endS = det(D) / 2;%计算离散曲率C(i-1) = 2*(Li+Li_1)^2 * S / (Li*Li_1 * Mi^3);end
end