1.概念及作用

设N为在节点矢量U={u_0，u_1，......，u_m}上的NURBS曲线，将U’∈[u_k，u_k+1]插入曲线N中，生成新的节点矢量U={u'_0 = u_0，......，u'_k = u_k，u'_k+1= u_k，......，u'_m+1= u_m}，此时仅改变向量空间基底，并不改变曲线的几何和参数化信息。

通俗点讲，节点插入就是在曲线的节点矢量中新增一个节点，该节点既可以插入在原有两节点之间，也可以重复插入在某一原有节点上。在插入一个节点后，原有的曲线形态不发生改变，但会影响被插入部分的局部曲线控制点的位置（原因在后文解释）。

2.原理及流程

节点插入实例如下图3次Nurbs（p = 3）所示，其中Pi(i∈0~6)为插入前控制点，红色标记为插入前节点矢量Uk[0,0,0,0,1,2,3,4,5,5,5,5]，图下方横轴表示节点矢量轴，每一个标记为一个节点，紧密相邻的节点表示在该处有重复节点。现向其中插入节点U_Bar=2.5，由于U5 < U_Bar < U6，故插入位置k=5（如图中蓝色节点所示）。

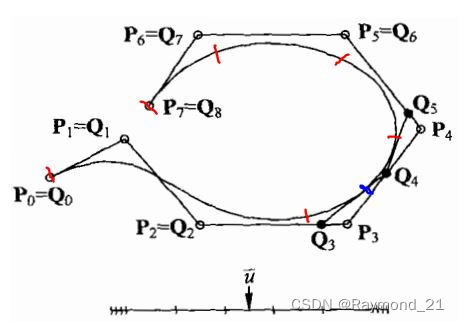
插入该节点后，为了保证曲线形态保持不变，会进行哪些操作呢？

1）修改插入位置所在曲线的控制点

根据Nurbs曲线的局部性可知，相邻节点间的曲线由p+1个控制点控制（图中节点U5-U6段对应控制点P2~P5）。当向这段曲线间插入一个节点时，首尾控制点的α值分别为1和0（图中P2和P5）,故Q2 = P2，Q6 = P5，这两点不发生改变，内部p+1-2个控制点会因1个节点的插入而增加为p+1-2+1个控制点（即图中控制点P3和P4会经重新计算生成Q3、Q4、Q5），新生成的控制点计算公式为（公式推导可参考The NURBS book-Chapter.5.2）：

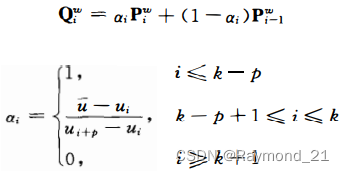
上述公式可以看出，先由相关被插入的节点U_Bar和相关的U计算出α，再根据α重新由相邻控制点计算出新的控制点。

概括一下：由于新增节点，会导致该节点位置所在曲线的原有控制点发生改变，计算生成p个新的控制点。

2）修改受影响控制点的权值

其实2）对于有一定基础的人来说应该是放在1）中一起讲的，但不幸本人在刚开始学习的时候毫无基础，在权值这里踩了大坑，因此认为分开讲对于初学者来说会更容易理解些。

请仔细看1）中的公式，这里的Q和P右上角都带了w（带有权值），其实这里每个控制点不单单包含三维空间中的x，y，z，它实际上是四维的，其中还包含了权值w，因此，除了受影响的p+1-2+1个控制点需按上述公式计算外，每个控制点本身对应的权值也需要按同样的方法计算。并且在控制点的计算过程中，新控制点不能单单的通过相邻控制点的x，y，z值得到，还需要将原本的权值也纳入公式计算，并在新的控制点生成后，将其除以权值。（这里但看有些抽象，可以结合文末的代码一起看）

概括一下：不仅权值需要按上述公式计算，由于控制点是四维的，控制点的计算过程中也需代入权值。

3）原节点矢量中新增目标节点

这部分就比较简单，因为新插入了一个节点U=2.5，原有的节点向量中要在k=5的位置新加入这个节点。

3.源码加注释

//向Nurbs中插入新的控制点，返回新的曲线
//输入：Nurbs曲线，插入的节点值，位置（从0开始），重复度（插入前的重复度），插入次数
NURBSpline InsertPoint(const NURBSpline& Sp1, double u, int k, int s, int r) {std::vector<double> w_aft(Sp1.n + r);	//插入后的权值std::vector<double> w_tem(Sp1.k - s + 1);	//插入影响的权值int U_num1 = Sp1.n + Sp1.k + 1, U_num2;	//插入前Sp1节点个数和插入后Sp2节点个数int C_num2 = Sp1.n + r;	//插入后Sp2的控制点个数std::vector<POINT> C_aft(Sp1.n + r);	//插入后的控制点容器std::vector<double> U_aft(C_aft.size() + Sp1.k + 1);	//插入后的节点容器//为节点赋值for (int i = 0; i <= k; i++) U_aft[i] = Sp1.U[i];	//插入点前面不受影响的部分for (int i = 1; i <= r; i++)  U_aft[k + i] = u;	for (int i = k + 1; i < U_num1; i++) U_aft[i + r] = Sp1.U[i];	//插入点后面不受影响的部分//为控制点赋值for (int i = 0; i <= k - Sp1.k; i++) {		//插入点前面不受影响的部分C_aft[i] = Sp1.ControlPoint[i]; w_aft[i] = Sp1.w[i];}for (int i = k - s; i < Sp1.n; i++) {		//插入点后面不受影响的部分C_aft[i + r] = Sp1.ControlPoint[i];w_aft[i + r] = Sp1.w[i];}//新生成的控制点赋初值std::vector<POINT> C_tem(Sp1.k - s + 1);for (int i = 0; i <= Sp1.k - s; i++) {C_tem[i] = Sp1.ControlPoint[k - Sp1.k + i];w_tem[i] = Sp1.w[k - Sp1.k + i];}//插入r次int L;for (int j = 1; j <= r; j++) {L = k - Sp1.k + j;	//此次插入位置for (int i = 0; i <= Sp1.k - j - s; i++) {			//计算控制该段曲线的k+1个控制点double alpha = (u - Sp1.U[L + i]) / (Sp1.U[i + k + 1] - Sp1.U[L + i]);C_tem[i].x = alpha * C_tem[i + 1].x * w_tem[i + 1] + (1.0 - alpha) *     C_tem[i].x * w_tem[i];    //新的控制点xyz值C_tem[i].y = alpha * C_tem[i + 1].y * w_tem[i + 1] + (1.0 - alpha) * C_tem[i].y * w_tem[i];C_tem[i].z = alpha * C_tem[i + 1].z * w_tem[i + 1] + (1.0 - alpha) * C_tem[i].z * w_tem[i];w_tem[i] = alpha * w_tem[i + 1] + (1.0 - alpha) * w_tem[i];    //新的权值C_tem[i].x /= w_tem[i];    //将新的点除以新的权值C_tem[i].y /= w_tem[i];C_tem[i].z /= w_tem[i];}//重新计算的k+1个控制点中，首尾点不变C_aft[L] = C_tem[0];				C_aft[k + r - j - s] = C_tem[Sp1.k - j - s];w_aft[L] = w_tem[0];w_aft[k + r - j - s] = w_tem[Sp1.k - j - s];}//载入剩下的控制点和权值for (int i = L + 1; i < k - s; i++) {C_aft[i] = C_tem[i - L];w_aft[i] = w_tem[i - L];}//由新生成的点、权值、节点构建新的NURBS曲线NURBSpline Nt(C_num2, Sp1.k);Nt.ControlPoint = C_aft;Nt.U = U_aft;Nt.w = w_aft;return Nt;
}

4.补充

1）本篇文章的实例是向节点间插入新的节点，但实际上还可以向节点上插入重复的节点，如下图。此时可以观察到，同样向3次曲线插入了1个节点，这次却只有两个控制点改变，除首尾控制点外还有一个控制点没发生改变，这是因为重复插入节点时，有一个控制点在代入公式计算时，U_Bar和Ui相等了，从而得到结果α=0，使得该控制点未发生改变。