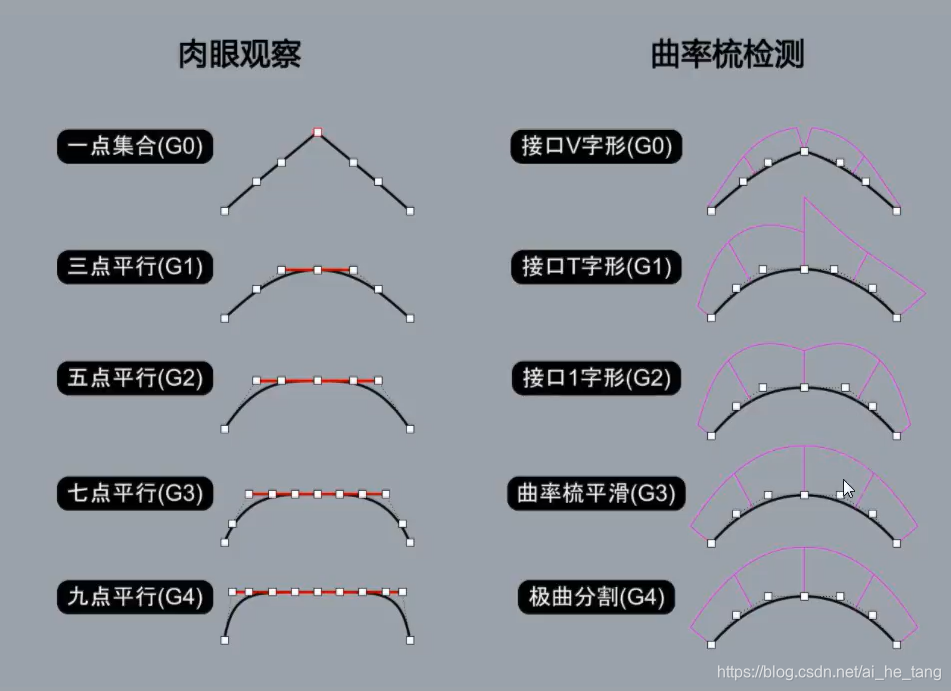
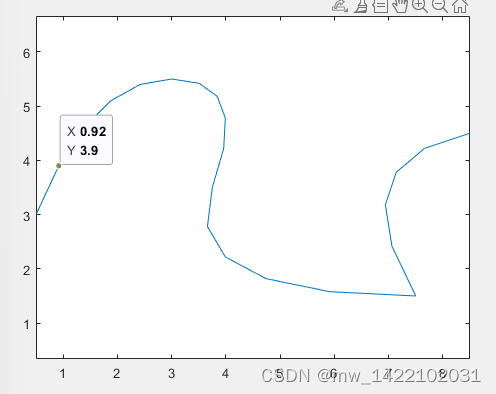
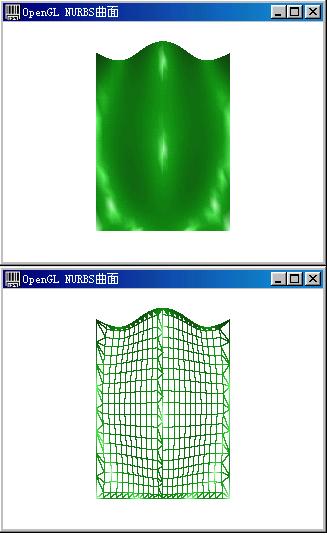
离散数据点NURBS曲线拟合算法

问题描述：对于离散数据点集来说，其主要特征点一般可以描述原始曲线轨迹的基本形状。对于大量的离散数据点来说，提取主要的特征点后在进行曲线拟合，这样可以降低计算次数，极高拟合效率。

可以描述原始曲线几何形状的特征点主要有反曲点、曲率极值点和弓高特征点。

提取主要特征点

反曲点：又称拐点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。

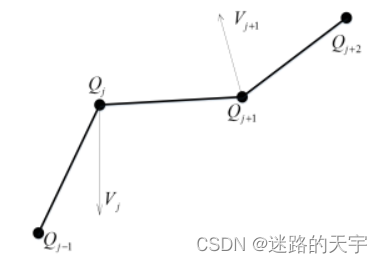
对于离散的数据点，相邻两点的法向量夹角值若为 $\pi$ ，则认为其凹凸性发生了变化。空间中每连续四个刀位点（ $Q_{j-1},Q_{j},Q_{j+1},Q_{j+2}$ ）,可以计算法向量 $V_{j},V_{j+1}$ ,如图1所示，并计算 $V_{j},V_{j+1}$ 的夹角 $\theta_{V}$ 。如果 $\theta_{V}>\theta_{max}$ （假设 $\theta_{max}=\pi/2$ ）,则曲线的凹凸性发生了变化，将该点作为反曲点，此时法向量 $V_{j},V_{j+1}$ 的夹角为一个接近于 $\pi$ 的值。通过遍历所有离散点，即可找到所有的反曲点。计算公式为： $\begin{Bmatrix} V_{j} =Q_{j-1}\cdot Q_{j}\times Q_{j}\cdot Q_{j+1} \\ V_{j+1}=Q_{j}\cdot Q_{j+1}\times Q_{j+1}\cdot Q_{j+1} \end{Bmatrix}$ , $\theta_{V}=arccos(\frac{V_{j}\times V_{j+1}}{\left | V_{j} \right |\left | V_{j+1} \right |})$

图1 反曲点示意图

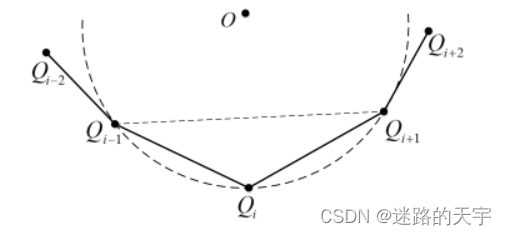
曲率极值点：本文采用圆弧估算法求解离散数据点的曲率，如图2所示，数据点 $Q_{i}$ 处的曲率值 $\kappa _{i}$ ,可以通过求解过点 $Q_{i-1},Q_{i},Q_{i+1}$ 的圆弧的曲率来求解，计算公式为： $\kappa _{i}=\frac{2sin(\angle Q_{i-1}Q_{i}Q_{i+1}))}{\left | Q_{i-1} Q_{i+1}\right |}$

图2 圆弧法估算曲率示意图

在确定了离散数据点的反曲点之后，遍历所有的反曲点，依次计算相邻两个反曲点之间个数据点的曲率值 $\kappa _{i}$ ，并计算相邻两点之间的曲率变化平均值 $k_{average}$ 作为曲率变化阈值，根据以下方式提取局部曲率极大值点

$\left\{\begin{matrix} k_{i}>k_{i-1}&&k_{i}>k_{i+1} \\ k_{i}>k_{average} \end{matrix}\right.$

弓高特征点：利用点距准则获取离散数据点中的弓高特征点，使得得到的主特征点更能体现原始轨迹的几何特征。如图3所示， $M_{j},M_{j+1}$ 为提取过反曲点的曲率极值后的两个相邻的主特征点，依次计算相邻两个主特征点之间的其他数据点到线段 $M_{i}M_{i+1}$ 的最大距离 $d_{k}$ ,设置最大距离 $d_{max}$ ,如果改点 $d_{k}>d_{max}$ ,则点 $Q_{k}$ 为弓高特征点，并将其作为主特征点，随后在 $M_{i}Q_{k}$ 和 $Q_{k}M_{i+1}$ 之间递归计算，依次获取 $M_{i},M_{i+1}$ 之间的所有弓高特征点，并将其作为主要特征点。

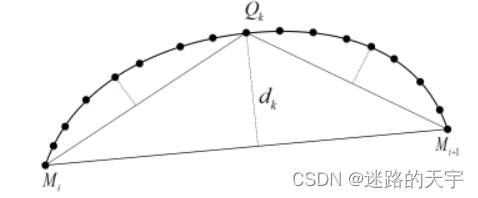
图3 弓高特征点示意图

通过提取反曲点、曲率极值点和弓高误差点，并将这些点作为主要特征点进行拟合即可得到原始曲线大致形同的轨迹，Matlab代码如下:

% 输入参数: data--原始数据点
% 输出参数：T--特征点
%           nummer--特征点在原始数据点中的序号
function [T, nummer] = ExtractFeaturePoints(data)% 记录特征点序号
nummer = [1];
T = zeros(71, 3);
T(1, :) = data(1, :);
% 设置夹角参数误差
thetaMax = pi / 2;
%% 提取反曲点
v = []; k = [];
for i = 2 : length(data) - 2V(i, :) = cross(data(i - 1, :) .* data(i, :), data(i, :) .* data(i + 1, :));V(i+1, :) = cross(data(i, :) .* data(i + 1, :), data(i + 1, :) .* data(i + 2, :));thetaV = acos(cross(V(i, :), acos(V(i + 1, :))) / (norm(V(i, :)) * norm(V(i + 1, :))));if thetaV >= thetaMaxnummer = [nummer, i];
%         temp = i;
%         % 遍历相邻两个反曲点之间的数据点
%         for j = nummer(length(nummer) - 1) + 1 : temp - 1
%             thetaQ = dot((data(j, :) - data(j - 1, :)), data(j + 1, :) - data(j, :)) / (norm(data(j, :) - data(j - 1, :)) * norm(data(j + 1, :) - data(j, :)));
%             k(j) = 2 * sin(thetaQ) / norm(data(j + 1, :) - data(j - 1, :));
%         end
%         for j = nummer(length(nummer) - 1) + 1 : temp - 1   %寻找两个反曲点之间的曲率极值点
%             if k(j) > k(j - 1) && k(j) > k(j + 1)
%                 j
%                T = [T; data(j, :)];
%             end
%         endT(i, :) = data(i, :);   end
end
nummer = [nummer, length(data)];
T(length(data), :) = data(length(data), :);%% 曲率极值点
k = [];                    
for i = 1 : length(nummer) - 1  for j = nummer(i) + 1 : nummer(i + 1) - 1thetaQ = dot((data(j, :) - data(j - 1, :)), data(j + 1, :) - data(j, :)) / (norm(data(j, :) - data(j - 1, :)) * norm(data(j + 1, :) - data(j, :)));k(j) = 2 * sin(thetaQ) / norm(data(j + 1, :) - data(j - 1, :));end
end 
k = [k, 0];
kAverage = mean(k);
for i = 2 : length(k) - 1if k(i) > k(i - 1) && k(i) > k(i + 1) && k(i) > kAverage% 记录主特征点对应的序号，并对序号进行升序排列nummer = sort([nummer, i]);T(i, :) = data(i, :);end
end%% 弓高特征点
dMax = 1.5;
i = 1;
flag = 0;
while i <= length(nummer) - 1j = nummer(i) + 1;rightTemp = nummer(i + 1) - 1;while j < rightTempd = PointToLineDistance(data(j, :), data(nummer(i), :), data(nummer(i + 1), :));j = j + 1; if d > dMaxnummer = sort([nummer, j - 1]);T(j - 1, :) = data(j - 1, :);j = j - 1;flag = 1;breakendendif flag%i = 1;flag = 0;elsei = i + 1;endend

自适应添加拟合误差点

通过主要特征点拟合得到的曲线并不能保证所有数据点都达到精度要求，因此需要通过计算每个数据点与拟合曲线的拟合误差，自适应的将拟合误差最大且超过给定精度的点作为主特征点，重新进行曲线的拟合。

在进行NURBS曲线拟合误差计算之前，首先要计算数据点的节点矢量，本文使用积累弦长参数化方法，得到第i个数据点对应的节点矢值u(i)。

根据两相邻主特征点，采用二分节点矢量法求点到NURBS曲线的最小距离。原始数据点data_i距离特征点 $M_{i}$ 的距离记为dLeft，对应的节点矢量记为uLeft；原始数据点data_i距离特征点 $M_{i+1}$ 的距离记为dRight,对应的节点矢量记为uRight。

如果dLeft > dRight,则更新左端点对应的节点参数uLeft = (uLeft+ uRight) / 2;

否则更新右端点对应的节点参数uRight = (uLeft+ uRight) / 2;

通过上述方式找到距离最近的点对应的节点值uMiddle,通过节点值uMiddle计算对应的NURBS曲线上的点，即可得到数据点data_i距离NURBS曲线的最近距离；通过计算 $M_{i},M_{i+1}$ 中各数据点与拟合曲线的误差值，从中找出最大误差diatanceMax，如果最近距离distanceMax > dmax（给定的误差上限）,则将该点也作为主特征点，重新进行NURBS曲线拟合。遍历所有相邻主特征点之间的原始数据点，找出每段中拟合误差的最大值，并将拟合误差大于误差上限的点添加到主特征点集中，重新进行NURBS拟合，由NURBS曲线的局部支撑性可知，新添加的主特征点不仅可以改善局部的拟合质量，还不会影响其他已经符合要求的区域。

以下为第一段曲线的自适应拟合误差提取代码;

% 输入参数: data--原始数据点
%           points--主要特征点
%           u--特征点的节点矢量
%           dd--控制顶点
% 输出参数：T--特征点
%           nummer--特征点在原始数据点中的序号
function [T, nummer] = DichotomyToFindDistance(points, data, u, U, nummer, dd)T = points;%% 第一段曲线% 以第一段曲线的两端点对应的参数u作为二分区间的左右端点flag = 1;while flagDistance = [];orderNummer = []; for i = nummer(1) + 1 : nummer(2) - 1uLeft = u(nummer(1)); %记录左端点对应的参数u uRight = u(nummer(3)); % 记录右端点对应的参数u% 计算第i个点距离左右端点的距离dLeft = norm(data(i, :) - data(nummer(1), :));dRight = norm(data(i, :) - data(nummer(2), :));% 二分区间法求第i个点距离第一段曲线的距离while uRight - uLeft > 1e-4if dLeft > dRight % 更新区间左端点参数uuLeft = (uLeft+ uRight) / 2;pointLeft = Curve(uLeft, U, 3, 0, dd);dLeft = norm(data(i, :) - pointLeft(1, :));else  % 更新区间右端点参数uuRight = (uLeft+ uRight) / 2;pointRight = Curve(uRight, U, 3, 0, dd);dRight = norm(data(i, :) - pointRight(1, :));endenduMiddle = (uLeft + uRight) / 2;pointMiddle = Curve(uMiddle, U, 3, 0, dd);% 第i个点距离第一段曲线的最近距离distance = sqrt((data(i, 1) - pointMiddle(1))^2 + (data(i, 2) -         pointMiddle(2))^2 + (data(i, 3) - pointMiddle(3))^2);Distance = [Distance, distance]; % 记录第i的点到曲线的最近距离orderNummer = [orderNummer, i]; % 记录Distance中元素对应的序号end% 寻找Distance中最大值，并返回最大值和最大值对应的原数据点中的序号[value, position] = max(Distance);% 如果最大距离大于给定误差，则将改点添加到主特征点中，并记录在原始数据点中的序号% 设定误差为le-2if value > 1e-2flag = 1;nummer = sort([nummer, orderNummer(position)]);points(orderNummer(position), :) = data(orderNummer(position), :);elseflag = 0;endend
end