1. 定义

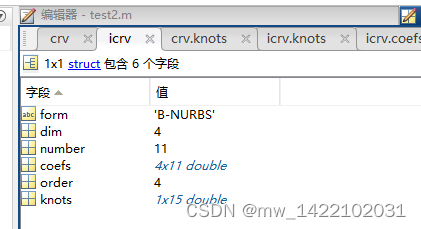
NURBS（Non Uniform Rational B-spline）曲线通常称为非均匀有理B样条曲线，其数学定义如下:

其中，

$N_{i,p}(u)$为$p$次B样条基函数，$P_0,P_1,...,P_n$为控制点, U = { $u_0,u_1,...,u_m$ }为节点向量, $w_0,w_1,..,w_n$代表权重.

推导过程:

容易得到以下结论:

1. 如果所有权重均等于1，NURBS 曲线退化成B样条曲线.
2. NURBS 曲线是有理曲线.

2. 性质

2.1 NURBS基函数的性质

1. $R_{i,p}(u)$是关于$u$的$p$次有理函数.
2. 如果$u\notin [u_i,u_{i+p+1})$，则$R_{i,p}(u)=0$
3. 当$u\in [u_i,u_{i+1})$时，至多存在$p+1$个$p$次基函数，即$R_{i-p,p}(u),R_{i-p+1,p}(u),...,R_{i,p}(u)$非0.
4. 当$u\in [u_i,u_{i+1})$时，$\sum _{j=i-p}^i{R}_{j,p}(u)=0$.
5. 如果节点数量为$m+1$，B样条基函数的次数为$p$，个数为$n+1$，则$m=n+1+p$.
6. 基函数$R_{i,p}(u)$在$k$重节点$u$处$C^{p-k}$连续.
7. 如果对所有的$i$，均有$w_i=c$，其中$c$是一个非0常量，则 $R_{i,p}(u)=N_{i,p}(u)$.

2.2 NURBS曲线的性质

1. NURBS曲线是次数为$p$的分段有理曲线组合.
2. $m=n+p+1$.
3. Clamped NURBS曲线经过$p_0$，$p_n$两个控制点.
4. 强凸包性:
   当$u\in [u_i,u_{i+1})$时，曲线段$C(u)$ 在由控制点$P_{i-p},P_{i-p+1},...,P_i$组成的凸包内.
5. 局部修改特性:
   改变控制点$P_i$的位置，只会影响处在$[u_i,u_{i+p+1})$区间内的曲线段$C(u)$.
6. $C(u)$在$k$重节点$u$处$C^{p-k}$连续.
7. 变差递减性.
8. B样条曲线和贝塞尔曲线是NURBS曲线的特例.
9. 投影不变性.

3. 修改权重

增加（或，减少）权重值会将曲线拉向（或，远离）控制点$P_i$。当$w_i$值无穷大时，曲线通过控制点$P_i$，当$w_i$为零时，控制点$P_i$对曲线无影响。

进一步推导:







可得以下结论：
如果$w_k$为非负，则$C(u)$始终位于$C^0(u)$和$P_k$的线段上，其中$C^0(u)$是$w_k=0$对应的点，$u$在$[u_k,u_{k+p+1}]$中。并且，当$w_k$从0变为无穷大时，$C(u)$从$C^0(u)$移到$P_k$，如果$w_k$是无穷大，$C^0(u)$变成$P_k$。
示意图：

4. 相关算法

4.1 节点插入：单点插入

假设有$N+1$个控制点$P_0，P_1，\dots ，P_n$，其相关权值分别为$W_0，W_1，\dots ，W_N$，节点向量为$U$，次数$p$.
令$P_i=(x_i，y_i，z_i)$，则控制点$P_i^W=(w_i{x}_i,w_i{y}_i,w_i{z}_i,w_i)$，$0<=i<=n$，节点向量$U$定义了一个$p$次的四维B样条曲线。在这个四维B样条曲线中插入一个新的节点$t$，得到一组新的控制点$Q_i^W=(X_i,Y_i,Z_i,W_i)$，$0<=i<=n$。通过将$Q_i^W$的前三个分量除以第四个分量，将$Q_i^W$投影回三维空间，得到给定NURBS曲线的新的控制点集。

4.2 De Boor’s Algorithm

只需将每个控制点乘以其权重，将NURBS曲线转换为4D B样条曲线，在此4D B样条曲线上执行de Boor算法，然后通过将前三个分量除以第四个分量，并保留第四个分量作为其新权重，将生成的曲线投影回3D。

5. Rational Bézier Curves

有理贝塞尔曲线:

6. Rational Bézier Curves: Conic Sections

构建圆锥曲线:
示意图:

计算：

抛物线:

椭圆：

双曲线：

结论：
由三个非共线控制点$P_0、P_1和P_2$定义的有理Bézier曲线，当$w$大于、等于或小于1时，分别为双曲线、抛物线或椭圆。

7. Circular Arcs and Circles

周期性的弧或圆:
示意图:

计算:




结果：

完整圆的构建: