人们对计算几何最常见的误解之一与曲线参数有关。
由于 Nurbs 曲线的数学相当复杂——其中大部分肯定超出了高中水平——很难解释控制点坐标、控制点权重、曲线度数和结向量如何共同使 nurbs 曲线的参数化变得复杂。 我自己对 Nurbs 数学的掌握充其量是皮毛,所以我认为如果我使用更简单的曲线类型开始这个讨论,对每个参与的人都会更好。

推荐:用 NSDT场景设计器 快速搭建3D场景。
但在我们开始讨论这个问题之前,我们应该首先为什么样的形状符合“曲线”的条件制定一些基本规则:
- 曲线是有限的一维对象,存在于具有任意维数的某个空间中。 在这篇博文中,我将只关注我们都熟悉的二维和三维空间。
- 每条曲线必须恰好有两个端点。 不多也不少。
- 如果端点重合,则认为曲线闭合。
- 曲线内部不能有间隙,因为这会产生两个以上的端点。
- 曲线上不能有分支点,除非端点与曲线的某个内部点重合。
基本上,将所有可能的曲线想象成橡皮糖,你可以拉伸、弯曲、扭曲和扭结它们,但最终它只不过是一堆变形应用于一块直的耐嚼的粘液。 请注意,上面的定义不同于曲线的常见数学定义。 数学家往往更具包容性和严谨性。
由于所有曲线都有两个端点(我们称它们为起点和终点)我们也可以说曲线存在于一个数值区间(interval)或域(domain)内。 该域将包含两个端点之间的所有数字,包括两个端点 :
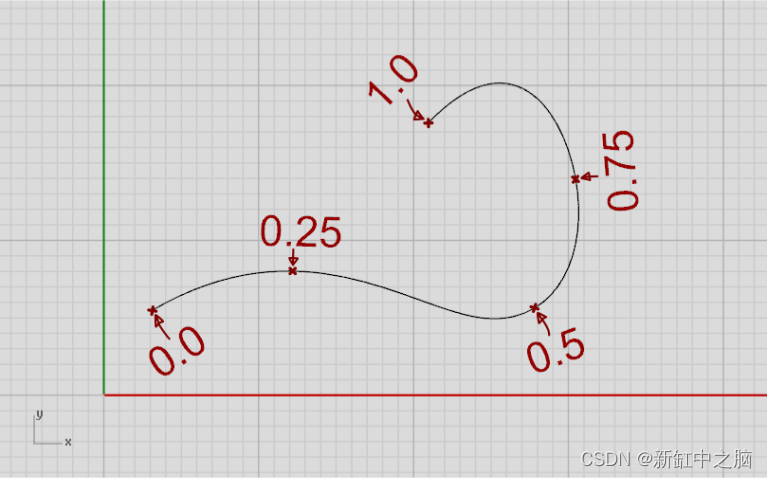
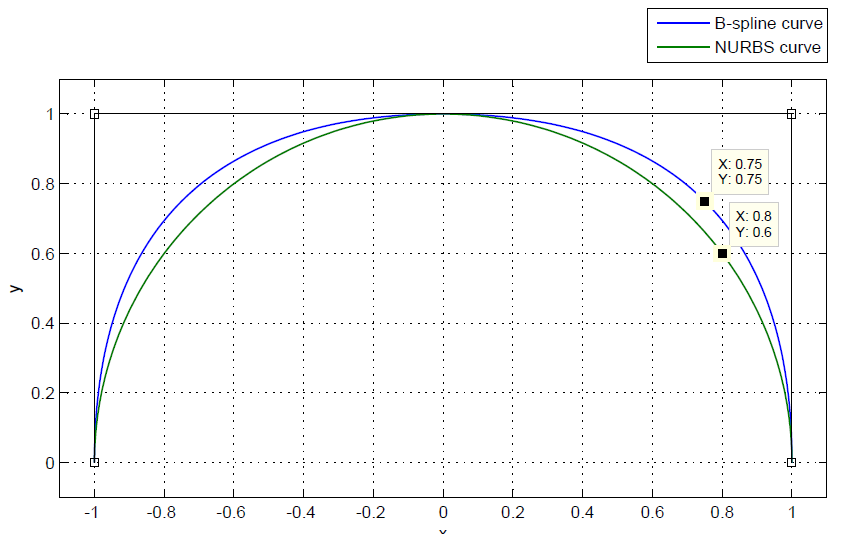
上图显示了域为 [0.0, 1.0] 的二维曲线。 0.0代表曲线的起点,1.0代表终点,0.0和1.0之间的每个数字代表曲线内部的某个点。 我选择了0.0和1.0,因为它们是整齐的数字,但每个具有非零长度的域在技术上都是有效的。 它可能是 [-π, +π] 或 [1000000.0, 1000000.1]。
让人困惑的第一件事是曲线的域与曲线的长度几乎没有关系。 你可以在不影响曲线的形状或大小的情况下更改域,并且可以在不影响域的情况下更改形状。 更糟糕的是,属于域某些部分的曲线量与该子域的大小几乎没有关系。 你可以在上图中看到,[0.25, 0.5] 子域中的曲线明显多于 [0.0, 0.25] 子域中的曲线。
那么什么是曲线参数以及曲线参数化的确切含义是什么? 每条数学曲线都由一些函数集合定义。 你可能非常熟悉的一个非常著名的函数是正弦函数,当绘制图形时,它会产生正弦波。 由于这是一条二维曲线,我们需要两个函数来描述它:
- x = t
- y = Sin(t)
第一个方程告诉我们曲线如何沿 X 轴运动,第二个方程定义了沿 Y 轴的行为。 这里的变量 t 称为参数。 曲线参数化是我们用来描述曲线参数属性的词,与几何属性相对。 参数化包括域和参数密度等内容,它定义了曲线任何部分的“速度”。 如果莫仍然认为曲线是有弹性的橡皮糖,那么曲线的“速度”就类似于橡皮糖的厚度。 曲线拉伸得越多,橡皮糖变得越稀薄,曲线速度就越高。
如果你想知道这条曲线在任何给定参数 t 的位置,你所要做的就是评估这两个函数并且你知道 t 处的坐标。 如果你想知道这条曲线在相同参数下的切向量,你计算的不是方程本身,而是它们的一阶导数,如果你想知道曲率,你可以使用二阶导数等等 。
如果我们求解这些方程以获得等间距 t 参数的集合,我们会得到如下结果:
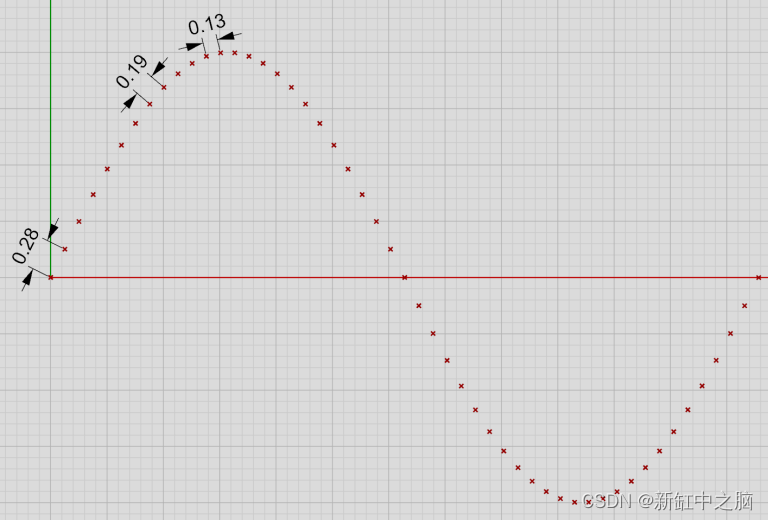
所有红点之间的水平距离相同,但垂直距离随正弦波而变化。 因此,两个相邻点之间的实际距离一直在变化。 当曲线以最大速度向上运动时,它可以高达 0.28,而当曲线在顶部变平时,它可以低至 0.13。 这是参数“密度”如何在曲线的不同部分变化的主要示例。
由于我们定义上述曲线的方式(使用正弦函数),在特定参数下对其进行评估非常简单快捷。 然而,以给定的长度对其进行评估非常困难且耗时。 找出哪个参数代表曲线上距离起点恰好 x 个单位的点所需的数学步骤数量是惊人的。 这就是为什么实际上 Rhino 和 Grasshopper 中的所有曲线方法都需要参数而不是长度。
因此,让我们看一下参数沿 Nurbs 曲线的进展,以了解它们在更复杂的几何类型中的行为方式。 看一下具有 3 个等距共线控制点的度数 = 2 的 nurbs 曲线:
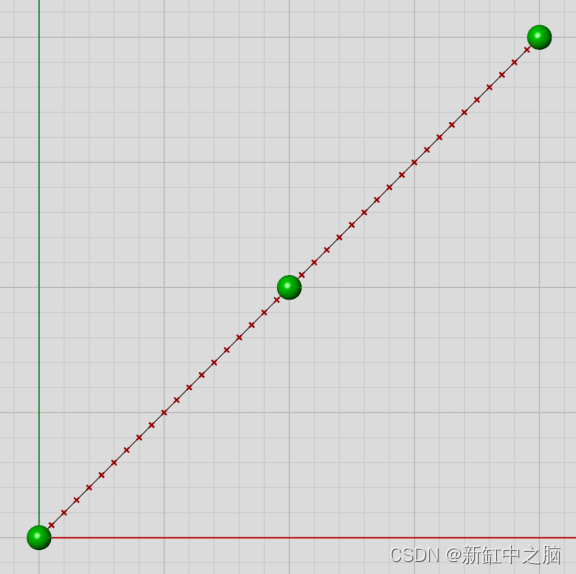
实际上看起来参数密度沿着这条曲线是恒定的。 这是因为控制点的完全对称性,任何会导致参数在一个地方拉伸的效果都会被相等且相反的效果所抵消。 但是,不要认为每条具有等距控制点的线性 nurbs 曲线都是如此整洁。 引入任何额外的复杂性和获得一致的参数密度将很难实现。 我们可以看到当我们将中间点从中心移开时会发生什么:
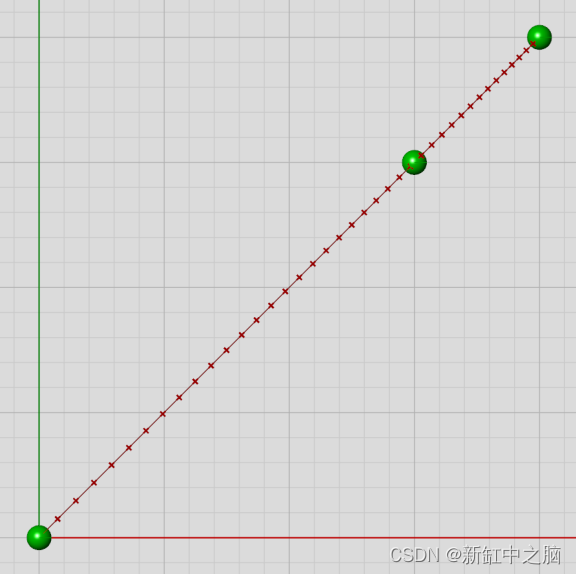
这导致曲线两端的平滑拉伸和压缩。 眼前的曲线形状和之前一模一样,只是不再是同一条曲线。 控制点的位置不是决定参数密度的唯一因素。 结向量(我们不会在这里讨论)和控制点权重也起着重要作用。 例如,此处中点的权重为 10.0,而端点的权重为 1.0:
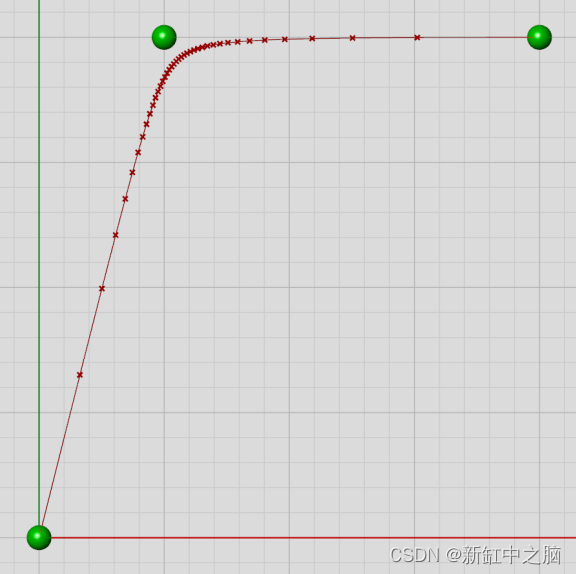
如果你要沿着这条曲线的长度随机选择一个点,你很可能会在相对笔直的地方。 但是,如果你选择一个随机参数,那么很可能会在急转弯的某个地方结束。 因此,根据你的迎角,这条曲线会显得非常弯曲或非常直。 当处理更高阶的 nurbs 曲线(degree=3 和 degree=5 非常流行)时,即使没有任何加权,也往往会在曲线末端附近出现明显的参数拉伸 。
那么既然我们已经讨论了正弦波曲线和 Nurbs 曲线,那么更简单的类型如直线、折线、圆和弧呢? 对于这些类型的曲线,实际上很容易以参数密度恒定的方式定义它们。 当以相等的 t 间隔对弧进行采样时,步长将保持不变。 不仅距离是恒定的,一阶、二阶、三阶等的导数也是完美无缺的:
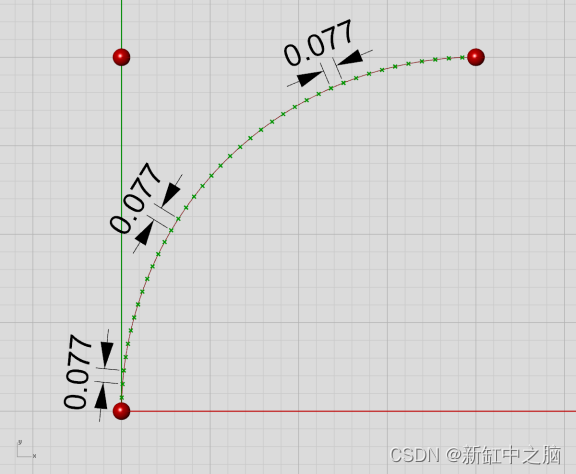
然而,将此弧线转换为 Nurbs 等价物(例如,通过在 Rhino 中打开控制点),所有美丽都会崩溃。 和以前一样,Nurbs 曲线的形状与圆弧的形状相同,但由于参数密度现在是可变的,导数也变得松散了:
所以,总结一下:
- 不要混淆曲线参数和曲线长度。
- 不要假设曲线的域必须有一个特定的值,它几乎可以是任何东西。
- 不要认为以相等的步长穿过曲线域意味着你也在以恒定速度沿着曲线移动。
- 具有相同形状的曲线可以具有截然不同的参数化。
原文链接:Nurbs参数空间 — BimAnt