CMP(比较)指令执行从目的操作数中减去源操作数的隐含减法操作,并且不修改任何操作数。
指令格式:
CMP 目的操作数, 源操作数
标志位 当实际的减法发生时,CMP指令按照计算结果修改溢出、符号、零、进位、辅助进位和奇偶标志位。如果比较的是两个无符号数,则零标志位和进位标志位表示的两个操作数之间的关系如下表所示:
| CMP结果 | ZF | CF |
|---|---|---|
| 目的操作数 < 源操作数 | 0 | 1 |
| 目的操作数 > 源操作数 | 0 | 0 |
| 目的操作数 = 源操作数 | 1 | 0 |
如果比较的是两个有符号数,则符号标志位、零标志位和溢出标志位表示的两个操作数之间的关系如下表所示:
| CMP结果 | 标志位 |
|---|---|
| 目的操作数 < 源操作数 | SF ≠ OF |
| 目的操作数 > 源操作数 | SF = OF |
| 目的操作数 = 源操作数 | ZF = 1 |
CMP指令是创建条件逻辑结构的重要工具。当在条件跳转指令中使用CMP时,汇编语言的执行结果就和IF语句一样。
以下是目的操作数 < 源操作数的举例:
; ZF CF
mov ax, 5
cmp ax, 10 ; 0 1

以下是目的操作数 = 源操作数的举例:
; ZF CFmov ax, 1000mov cx, 1000cmp cx, ax ; 1 0

以下是目的操作数 > 源操作数的举例:
;ZF CF
mov ax, 105
cmp ax, 0 ;0 0
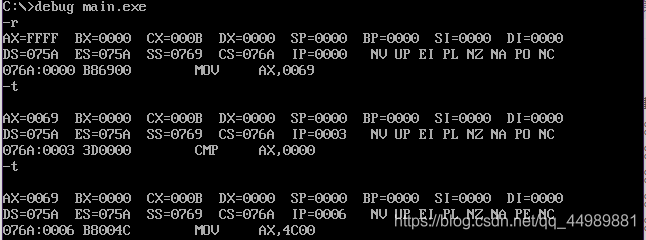
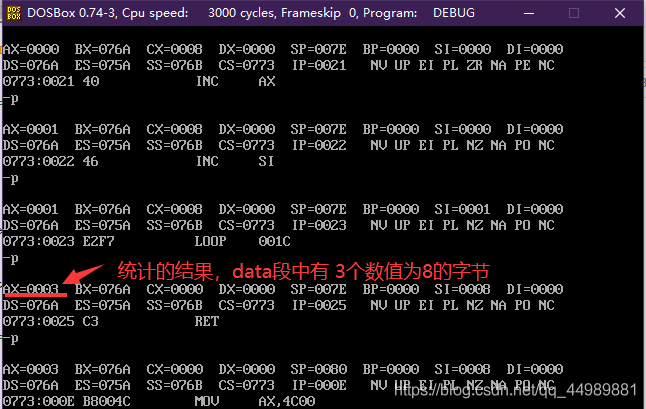
使用CMP指令统计data 段中数值为8的字节个数,用ax保存统计结果。
; 1.编程 统计data 段中数值为8的字节个数,用ax保存统计结果
assume cs:code, ds:data, ss:stackdata segmentdb 8, 11, 8, 1, 8, 5, 63, 38
data endsstack segment stackdb 128 dup(0)
stack endscode segmentstart: mov ax, stackmov ss,axmov sp, 128call init_regcall get_eightmov ax, 4C00Hint 21H;============================================
get_eight: mov si,0mov cx, 8mov ax, 0getEight: cmp byte ptr ds:[si], 8jne nextNumberinc ax
nextNumber: inc siloop getEightret
;===============================================
init_reg: mov bx, datamov ds, bxretcode endsend start
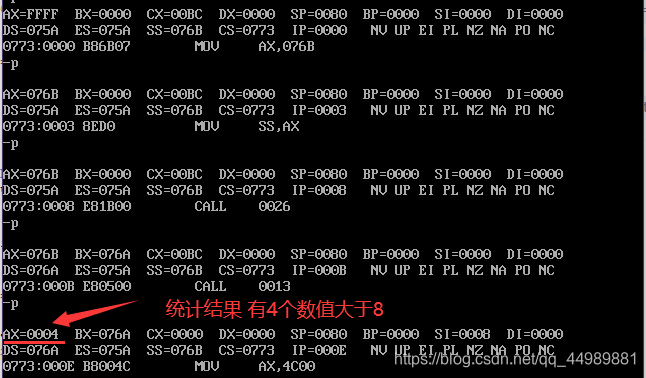
使用 CMP指令 统计data 段中数值大于8的字节个数,用ax保存统计结果
; 2.编程 统计data 段中数值大于8的字节个数,用ax保存统计结果
assume cs:code, ds:data, ss:stackdata segmentdb 8, 11, 8, 12, 8, 5, 63, 38
data endsstack segment stackdb 128 dup(0)
stack endscode segmentstart: mov ax, stackmov ss,axmov sp, 128call init_regcall get_eightmov ax, 4C00Hint 21H;============================================
get_eight: mov si,0mov cx, 8mov ax, 0getEight: cmp byte ptr ds:[si], 8jna nextNumber ; ja > na <=inc ax
nextNumber: inc siloop getEightret
;===============================================
init_reg: mov bx, datamov ds, bxretcode endsend start
| CMP ax, bx | 修改标志位 | 符号描述 |
|---|---|---|
| ax = bx | ZF = 1 | 相等 |
| ax != bx | ZF = 0 | 不相等 |
| ax < bx | CF = 1 | 小于 |
| ax >= bx | CF = 0 | 大于等于 |
| ax > bx | CF = 0 并且 ZF = 0 | 大于 |
| ax <= bx | CF = 1 或者 ZF = 1 | 小于等于 |
基于有符号的举例:
mov al, 1
mov bl, 2
cmp al, bl → 推理出来 al < bl
sub al, bl → 影响标志位 1 - 2 = -1 SF 符号标志位置1
mov al, 22H → 34 34 - (-96) = 140 -128 ~ 127
mov bl, A0H -96
sub al, bl → OF标志位 和 SF标志位 溢出标志位置1 符号标志位置1
mov al, 8AH -118 - 112 = - 230 溢出 1A 正数
mov bl, 70H
cmp al, bl OF = 1 SF = 0 溢出标志位置1 符号标志位置0
总结:基于有符号比较
设 cmp al, bl
如果 SF = 1 OF = 0
那么 al < bl如果SF = 1 OF =1
那么 al > bl如果 SF = 0 OF = 1
因为 SF = 0
不等式应该为 al - bl > 0 al > bl
当OF = 1 成立时,那么
al < bl如果SF = 0 OF = 0
那么 al - bl > 0
得到 al > bl
如果因为溢出导致了实际结果为负,那么逻辑上真正的结果必然为正。
如果因为溢出导致了实际结果为正,那么逻辑上真正的结果必然为负。
基于无符号数比较的跳转
| 助记符 | 说明 |
|---|---|
| JB | 小于跳转 |
| JNB | 不小于跳转 |
| JNBE | 不小于或等于跳转 |
| JA | 大于跳转 |
| JNA | 不大于跳转 |
| JNAE | 不大于或等于跳转 |
基于相等性的跳转
| 助记符 | 说明 |
|---|---|
| JE | 相等跳转 |
| JNE | 不相等跳转 |
| JCXZ | CX = 0 跳转 |
| JECXZ | ECX = 0 跳转 |
| JRCXZ | RCX = 0 跳转(64模式) |
基于有符号数比较的跳转
| 助记符 | 说明 |
|---|---|
| JG | 大于跳转 |
| JL | 小于跳转 |
| JNLE | 不小于或等于跳转 |
| JNGE | 不大于活等于跳转 |
| JGE | 大于或等于跳转 |
| JLE | 小于或等于跳转 |
| JNL | 不小于跳转 |
| JNG | 不大于跳转 |
基于进位和零标志位的跳转
| 助记符 | 说明 |
|---|---|
| JC | 进位跳转(进位标志位置1) |
| JNC | 无进位跳转(进位标志位清零) |
| JZ | 为零跳转(零标志位置1) |
| JNZ | 非零跳转(零标志位清零) |