1.时钟频率是什么？

时钟：顾名思义，时钟以精确和固定的时间间隔，触发电信号，其信号被控制单元用于推进CPU的内部操作。而CPU执行 取指令–解码–执行的速度为时钟速度（时钟频率）。
在各类CPU当中每执行一个程序或者指令其背后的物理电路的运行过程都是极其复杂的，而时钟的意义就是有序的让各单元完成操作，如同乐队指挥家的指挥节奏。所以说时钟是MCU的脉搏。

2.时钟周期

时钟周期也称为振荡周期，定义为时钟频率的倒数，单片机中最小的时间单位。
例如51单片机中，时钟频率是12MHz，那么它的时钟周期就是1/12us。
在51单片机中晶振频率没有分频就直接作为CPU频率使用，所以
时钟周期 = 晶振周期 = 振荡周期。

3.状态周期

在51单片机中把一个时钟周期定义为一个节拍（用P表示），二个节拍定义为一个状态周期（用S表示）。即两个时钟周期=状态周期。

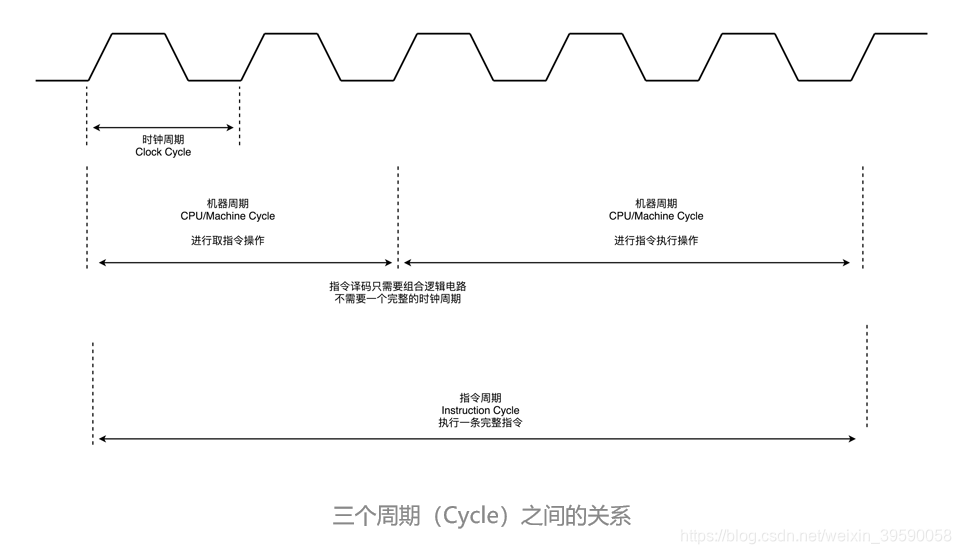
4.机器周期

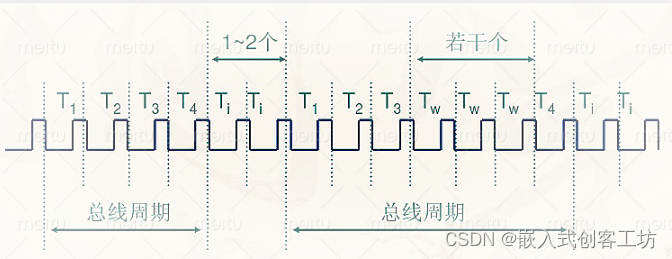
例如，取指令、存储器读、存储器写等，这每一项工作称为一个基本操作。完成一个基本操作所需要的时间称为机器周期。
51单片机的一个机器周期同6个S周期（状态周期）组成，即51单片机的机器周期由6个状态周期组成，也就是 机器周期=6个状态周期=12个时钟周期。
那么以12Mhz的振荡频率为例，一个机器周期的时长是1us。

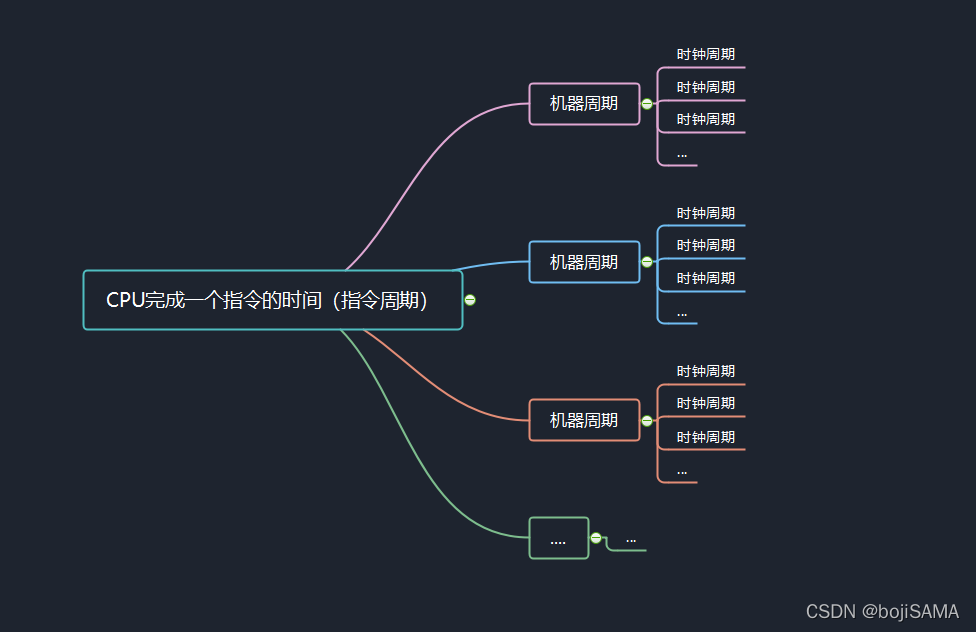
5指令周期

执行一条指令所需要的时间，一般由若干个机器周期组成。指令不同，所需的机器周期也不同。