前言
对无人机进行轨迹规划时,需要对可行空间进行数学表示,可行空间通常被表示为凸组合的形式。
结论
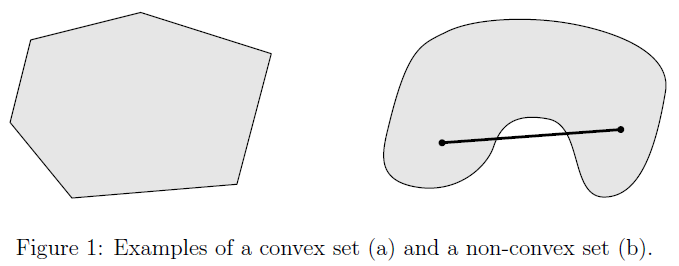
在 R n R^n Rn中的m个向量 a 1 , a 2 , a 3 , . . . . . , a m a_1,a_2,a_3,.....,a_m a1,a2,a3,.....,am的凸组合是它们在n维空间的最小凸包(在二维空间中凸组合是一堆点的所形成的最小凸多边形,在三维空间中凸组合是一堆点所形成的最小凸包)。


定义
设向量 { x i } \{x_i\} {xi}, i ∈ 1 , 2 , 3 , . . . . , n i\in1,2,3,....,n i∈1,2,3,....,n,存在 { λ i } \{\lambda_i\} {λi}, i ∈ 1 , 2 , 3 , . . . . , n i\in1,2,3,....,n i∈1,2,3,....,n, ∑ 1 n λ i = 1 \sum\limits_1^n\lambda_i=1 1∑nλi=1, 则称 ∑ 1 n λ i x i \sum\limits_1^n \lambda_i x_i 1∑nλixi称为 { x i } \{x_i\} {xi}的凸组合。
代码实现
搜到的回头自己写
在这里插入代码片
凸组合的几何含义
在这里说明凸组合在一维,二维,三维下的凸组合的几何含义(路径规划只用到这三个),更高维的可以类推
1. 直线上的情况
在直线上设有坐标为a,b的两点的凸组合x,则
x = λ a + ( 1 − λ ) b , 0 < λ < 1 x=\lambda a+(1-\lambda )b, 0<\lambda<1 x=λa+(1−λ)b,0<λ<1
λ = b − x b − a \lambda=\dfrac{b-x}{b-a} λ=b−ab−x
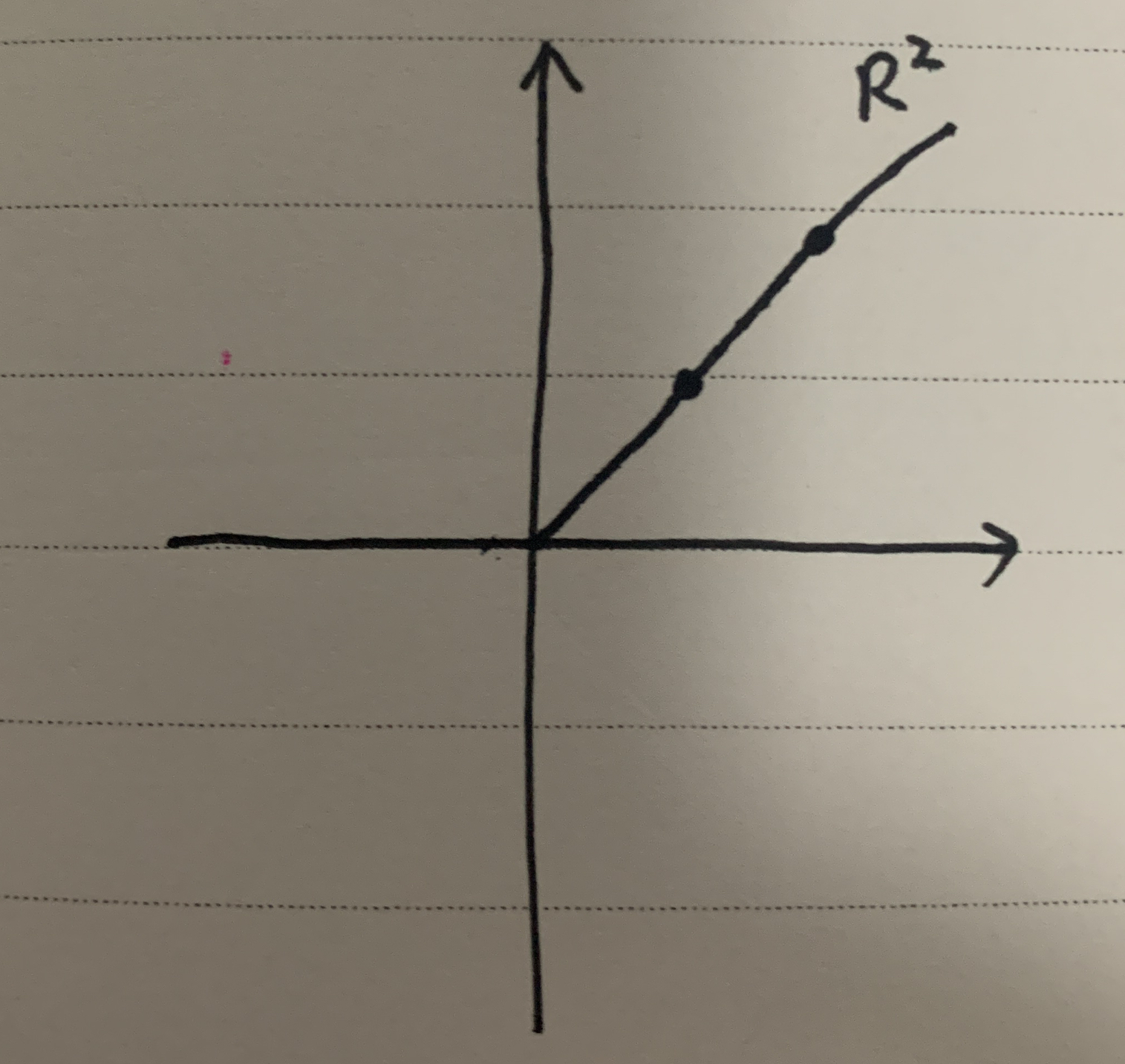
也就是说 0 < b − x b − a < 1 0<\dfrac{b-x}{b-a}<1 0<b−ab−x<1, x是在a和b之间的点,如图

2. 两个向量的凸组合
设 R 2 R^2 R2中的向量a(a_1,a_2), b(b_1,b_2) 的凸组合为x(x_1,x_2) , 则
x = λ a + ( 1 − λ ) b x=\lambda a+(1-\lambda )b x=λa+(1−λ)b
⇓ \Downarrow ⇓
x 1 = λ a 1 + ( 1 − λ ) b 1 x_1=\lambda a_1+(1-\lambda )b_1 x1=λa1+(1−λ)b1
x 2 = λ a 2 + ( 1 − λ ) b 2 x_2=\lambda a_2+(1-\lambda )b_2 x2=λa2+(1−λ)b2
这表示x 在连结 a,b两点的线段上, R 3 R^3 R3 中的情况也是一样
3. 三个向量的凸组合
还是在 R 2 R^2 R2中考虑三个点 a ( a 1 , a 2 ) , b ( b 1 , b 2 ) , c ( c 1 , c 2 ) a(a_1,a_2),b(b_1,b_2),c(c_1,c_2) a(a1,a2),b(b1,b2),c(c1,c2),的凸组合x(x_1,x_2,x_3),则
x = λ 1 a + λ 2 b + λ 3 c , λ 1 + λ 2 + λ 3 = 1 , λ 1 + λ 2 ≠ 0 x=\lambda_1a+\lambda_2b+\lambda_3c,\lambda_1+\lambda_2+\lambda_3=1,\lambda_1+\lambda_2\neq0 x=λ1a+λ2b+λ3c,λ1+λ2+λ3=1,λ1+λ2=0
⇓ \Downarrow ⇓
x = ( λ 1 + λ 2 ) ( λ 1 λ 1 + λ 2 a + λ 2 λ 1 + λ 2 b ) + λ 3 c x=(\lambda_1+\lambda_2)(\dfrac{\lambda_1}{\lambda_1+\lambda_2}a+\dfrac{\lambda_2}{\lambda_1+\lambda_2}b)+\lambda_3c x=(λ1+λ2)(λ1+λ2λ1a+λ1+λ2λ2b)+λ3c
令
d = λ 1 λ 1 + λ 2 a + λ 2 λ 1 + λ 2 b d=\dfrac{\lambda_1}{\lambda_1+\lambda_2}a+\dfrac{\lambda_2}{\lambda_1+\lambda_2}b d=λ1+λ2λ1a+λ1+λ2λ2b
d是a和b的凸组合,d在a和b的连线上, x = ( λ 1 + λ 2 ) d + λ 3 c x=(\lambda_1+\lambda_2)d+\lambda_3c x=(λ1+λ2)d+λ3c, x是d和c的凸组合,x在d和c的连线上,如图:

点数4个以上的情况也是同样的, { a 1 , a 2 , a 3 , . . . . . . , a n } \{a_1,a_2,a_3,......,a_n\} {a1,a2,a3,......,an}中n个点的凸组合全体形成一个凸多边形,这个凸多边形的顶点或者是a的全部
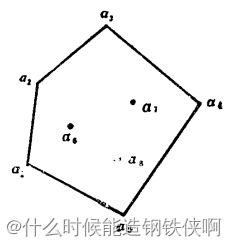
对于三维情况同理。
参考
百度百科 凸组合