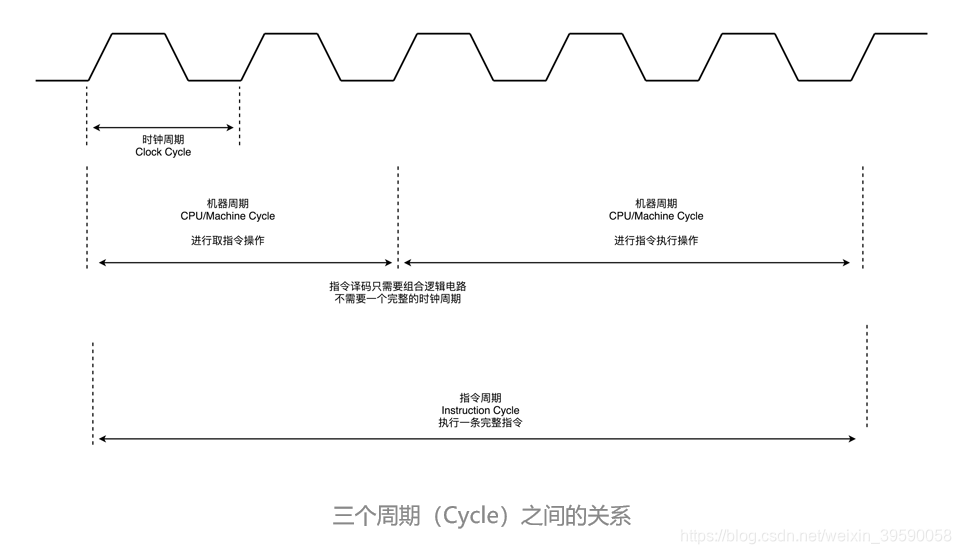
一、时钟周期

        时钟周期也称为振荡周期，定义为时钟脉冲的倒数(时钟周期就是单片机外接晶振的倒数，例如12M的晶振，它的时钟周期就是1/12us)，是计算机中的最基本的、最小的时间单位。在一个时钟周期内，CPU仅完成一个最基本的动作。时钟脉冲是计算机的基本工作脉冲，控制着计算机的工作节奏。时钟频率越高，工作速度就越快。     

二、指令周期

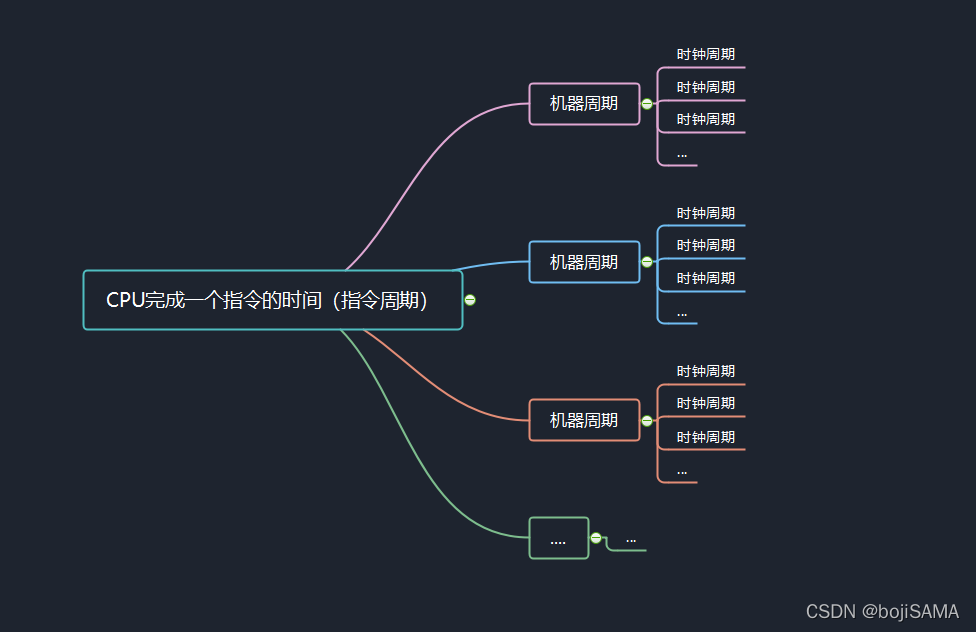
        指令周期：执行一条指令所需要的时间，一般由若干个机器周期组成。指令不同，所需的机器周期也不同。指令周期常常用若干个CPU周期数来表示，CPU周期也称机器周期。通常含一个机器周期的指令称为单周期指令，包含两个机器周期的指令称为双周期指令。

三、机器周期

        机器周期：计算机中，常把一条指令的执行过程划分为若干个阶段，每一个阶段完成一项工作(例如，取指令、存储器读、存储器写等)。每一项工作称为一个基本操作，完成一个基本操作所需要的时间称为机器周期。它一般由12个时钟周期（振荡周期）组成，即由6个状态周期组成，而振荡周期＝1/晶振频率，因此单片机的机器周期＝12/晶振频率

        8051系列单片机的一个机器周期由6个S周期（状态周期）组成，也就是说一个机器周期＝6个状态周期＝12个振荡周期（即时钟周期） 。

四、总线周期

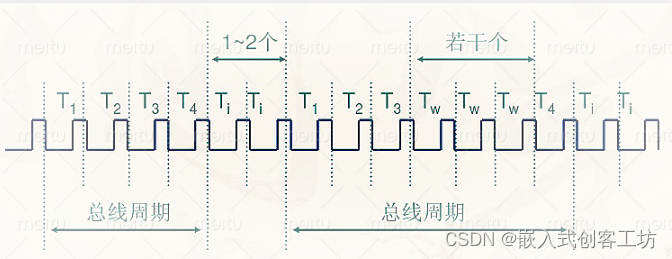
        总线周期：由于存贮器和I/O端口是挂接在总线上的，CPU对存贮器和I/O接口的访问，是通过总线实现的。通常把CPU通过总线对微处理器外部(存贮器或 I/O接口)进行一次访问所需时间称为一个总线周期。一个总线周期一般包含4个时钟周期，这4个时钟周期分别称4个状态即T1状态、T2状态、T3状态和 T4状态。 

        对总线周期，可能存在 空闲周期Ti和等待周期Tw。
        空闲周期Ti：在两个总线周期之间插入
        等待周期Tw：在总线周期T3和T4之间插入

 五、关系总结 

        简言之，它们之间的关系就是，指令周期由若干个机器周期组成，总线周期一般由4个时钟周期组成。

        机器周期和总线周期并无明确的相互包含关系。机器周期指的是完成一个基本操作的时间，这个基本操作有时可能包含总线读/写，因而包含总线周期，但是有时可能与总线读/写无关。

        指令周期是CPU的关键指标，指取出并执行一条指令的时间。一般以机器周期为单位，分单指令执行周期、双指令执行周期等。单片机的大部分指令（ARM、DSP）均采用单指令执行周期。

        周期就是时间，即完成一次任务的时间。