就工作方式而言,CPU 分两种:同步 CPU 和异步 CPU。异步 CPU并不常见,用途广泛的是同步 CPU 。
既然是同步 CPU,当然就需要有一个同步机制,或者说要有个“主管”来维护同步状态,不然你做一样,我做一样,没有统一协调,那不就乱套了?在计算机中,就是时钟发生器来完成这项工作——不停给芯片发送一个连续的脉冲信号,每一次脉冲到来,芯片内的晶体管就改变一次状态,让整个芯片完成一定任务。统一指挥,完成任务。
电脑中有许许多多的半导体芯片,这些芯片就是在时钟发生器发送的特定时钟频率下有条不紊进行工作的。

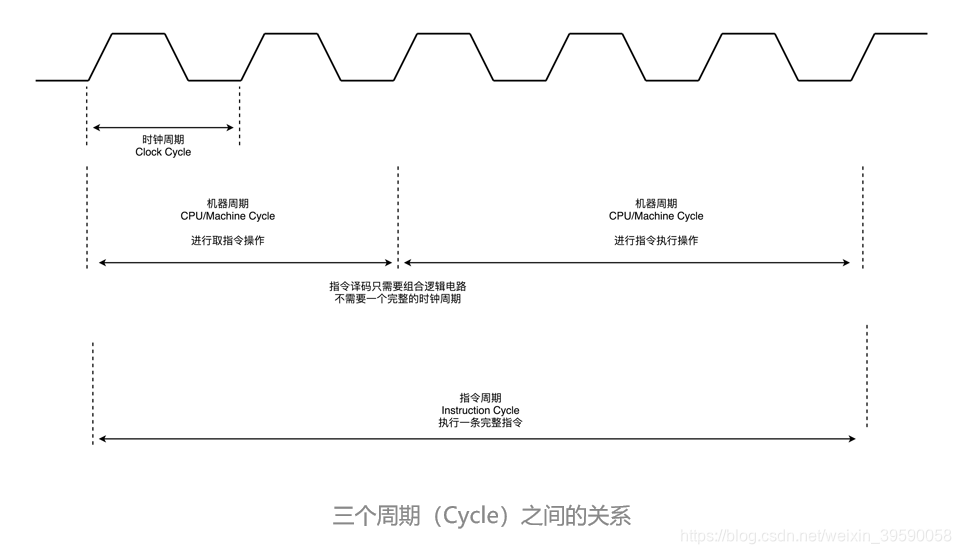
如图,时钟发生器发出的脉冲信号做出周期变化的最短时间称之为震荡周期,也称为 CPU 时钟周期。它是计算机中最基本的、最小的时间单位。
上面说到,每一次脉冲(即一个震荡周期)到来,芯片内的晶体管就改变一次状态,让整个芯片完成一定任务。一个震荡周期内,晶体管只会改变一次状态。由此,更小的时钟周期就意味着更高的工作频率。
一秒(1 s)内,震荡周期的个数称为时钟频率,俗称主频。
不难看出主频和时钟周期的关系:
时 钟 频 率 ( 主 频 ) = 1 C P U 时 钟 周 期 时钟频率(主频)= \frac{1}{CPU 时钟周期} 时钟频率(主频)=CPU时钟周期1
由上面的关系不难推出,主频越高,CPU的运算速度就越快。
每一款芯片都有自己的频率极限。因为电脑中的芯片绝大多数属于数字逻辑芯片,数字芯片中众多的晶体管全都工作在开关状态,它们的导通和关断动作无不是按照时钟信号的节奏进行的。如果时钟频率过高,就可能出现晶体管的状态来不及变化的情况,产生死锁或随机性误操作。
有的 CPU 芯片允许在短时间内提升时钟频率,即俗称的“超频”,以获得更好的性能。当然,如果长时间处于超频状态,将可能对芯片造成 irreparable 损伤。
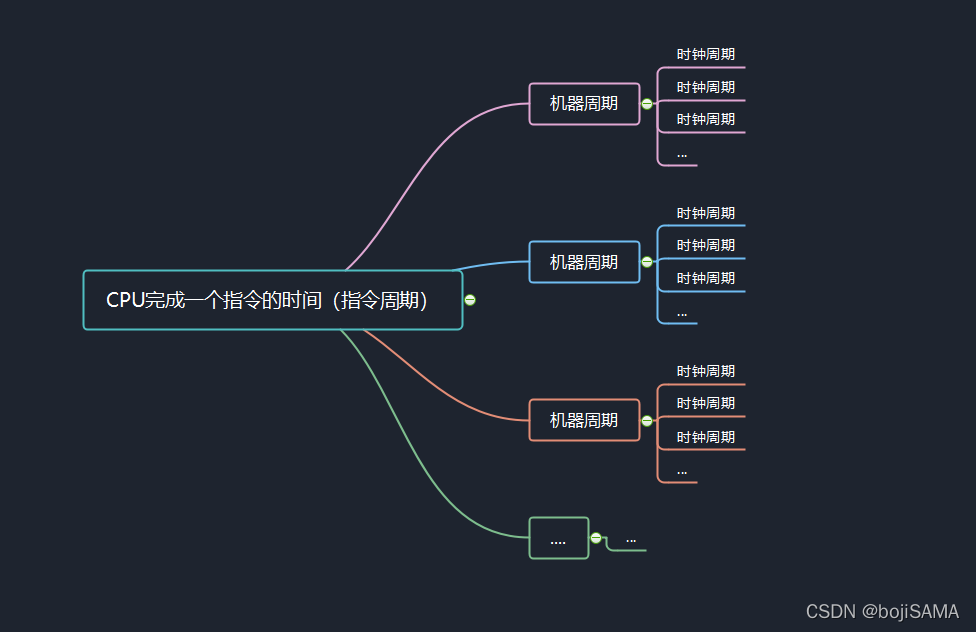
注意!主频越高,CPU的运算速度就越快。但主频不等于处理器一秒钟执行的指令条数,因为一条指令的执行可能需要多个时钟周期。