时钟周期
时钟周期也称为振荡周期,定义为时钟脉冲的倒数(可以这样来理解,时钟周期就是单片机外接晶振的倒数,例如12M的晶振,它的时间周期就是1/12 us),是计算机中最基本的、最小的时间单位。
在一个时钟周期内,CPU仅完成一个最基本的动作。对于某种单片机,若采用了1MHZ的时钟频率,则时钟周期为1us;若采用4MHZ的时钟频率,则时钟周期为250ns。由于时钟脉冲是计算机的基本工作脉冲,它控制着计算机的工作节奏(使计算机的每一步都统一到它的步调上来)。显然,对同一种机型的计算机,时钟频率越高,计算机的工作速度就越快。但是,由于不同的计算机硬件电路和器件的不完全相同,所以其所需要的时钟周频率范围也不一定相同。我们学习的8051单片机的时钟范围是1.2MHz-12MHz。
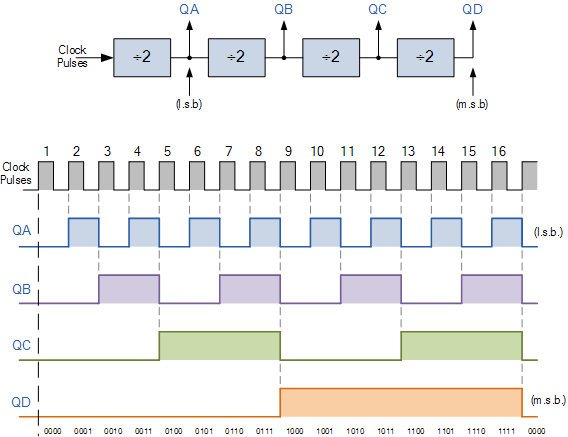
在8051单片机中把一个时钟周期定义为一个节拍(用P表示),二个节拍定义为一个状态周期(用S表示)。
机器周期
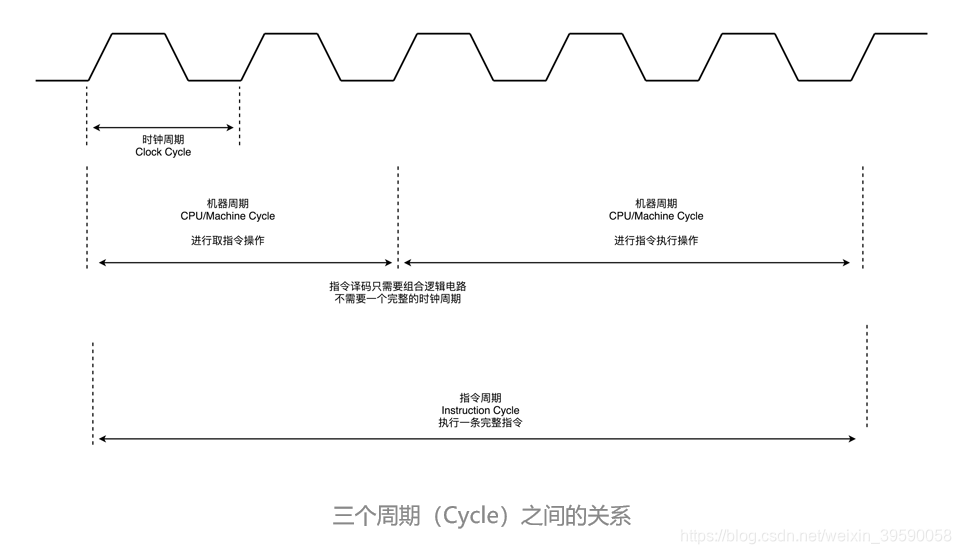
在计算机中,为了便于管理,常把一条指令的执行过程划分为若干个阶段,每一阶段完成一项工作。例如,取指令、存储器读、存储器写等,这每一项工作称为一个基本操作。完成一个基本操作所需要的时间称为机器周期。一般情况下,一个机器周期由若干个S周期(状态周期)组成。8051系列单片机的一个机器周期同6个S周期(状态周期)组成。前面已说过一个时钟周期定义为一个节拍(用P表示),二个节拍定义为一个状态周期(用S表示),8051单片机的机器周期由6个状态周期组成,也就是说一个机器周期=6个状态周期=12个时钟周期。
指令周期
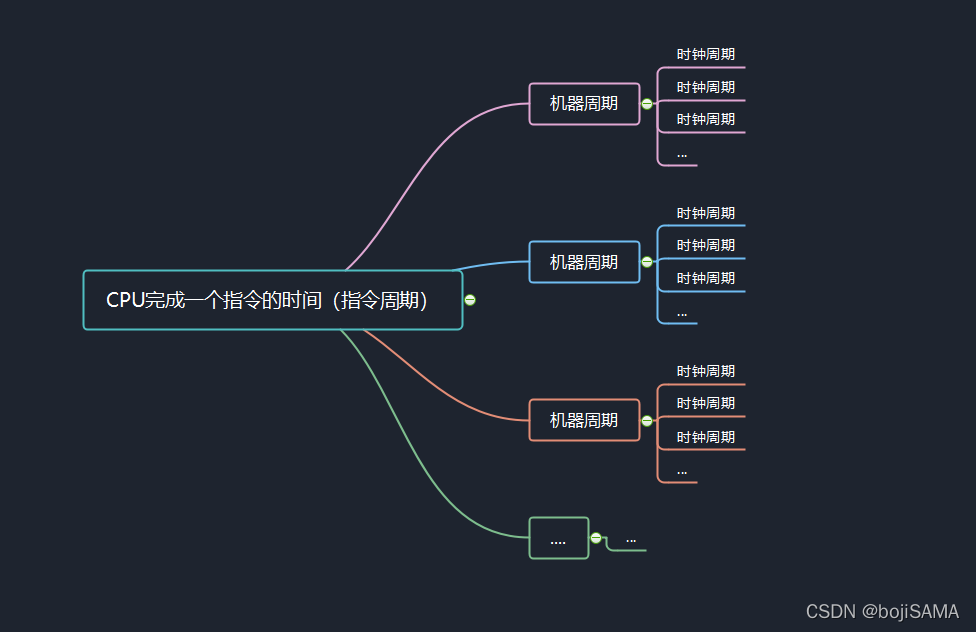
指令周期是执行一条指令所需要的时间,一般由若干个机器周期组成。指令不同,所需的机器周期数也不同。对于一些简单的的单字节指令,在取指令周期中,指令取出到指令寄存器后,立即译码执行,不再需要其它的机器周期。对于一些比较复杂的指令,例如转移指令、乘法指令,则需要两个或者两个以上的机器周期。
通常含一个机器周期的指令称为单周期指令,包含两个机器周期的指令称为双周期指令。
单片机中定时器(Timer)、计数器(Counter)区别:
定时器和计数器在单片机内部使用同一电路来实现:当这一电路选择为定时器功能时,其输入源通常来自于内部输入的单位时间脉冲(比如由时钟源产生),包含有时间的概念在里面;当这一电路选择为计数器功能时,其输入源通常来自于外部事件触发,用于统计外部事件的数量,没有时间概念在里面。