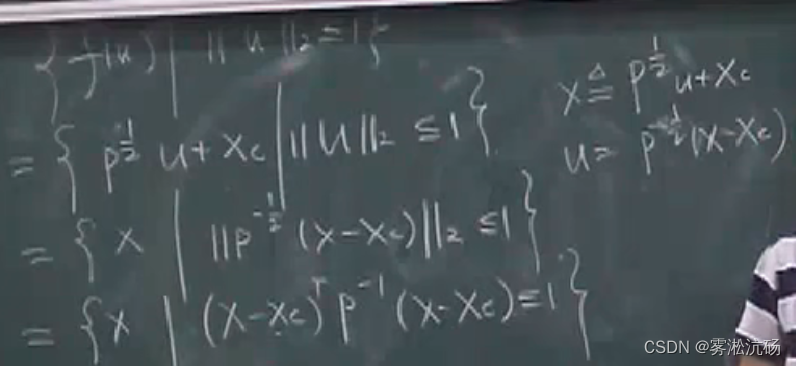凸集——几种重要的凸集
- 2.几种重要的凸集
- 2.1 超平面与半空间
- 2.2 球和椭球
- 2.3 多面体(关注单纯形)
- 2.4 半正定锥
- 2.5参考
Date: 2020/04/11
Editor:萧潇子(Jesse)
Contact: 1223167600@qq.com
2.几种重要的凸集
本节讲述一些重要凸集的概念,首先介绍一些简单的例子,我们不妨先来看一些特例:
- C = { x } C=\{x \} C={x} 单点
- 点是仿射集,凸集,原点是凸锥
- 空集是仿射集,凸集,凸锥
下面再来看几种重要的凸集:
- R n R^n Rn 仿射集、凸集、凸锥
- R n R^n Rn空间的子空间 仿射集、凸集、凸锥
- 任意直线 仿射集、凸集、凸锥(过原点)
- 任意线段 仿射集(点)、凸集、凸锥(原点)
- { x 0 + θ v ∣ θ ≥ 0 } \{x_0+\theta v|\theta\ge0\} {x0+θv∣θ≥0} x 0 ∈ R n x_0\in R^n x0∈Rn θ ∈ R \theta \in R θ∈R - v ∈ R n v\in R^n v∈Rn 射线 仿射集(v=0缩减为一个点) 、凸集、凸锥(过原点)
2.1 超平面与半空间
超平面
定义: { x ∣ a T x = b } \{x|a^Tx=b\} {x∣aTx=b} x , a ∈ R n x,a\in R^n x,a∈Rn, b ∈ R b\in R b∈R, a ≠ 0 a\neq0 a=0
性质: 仿射集、凸集、凸锥(过原点)
半空间
定义: a T x ≤ b , a T x ≥ b a^Tx\le b,\quad a^Tx\ge b aTx≤b,aTx≥b
性质: 凸集、凸锥(过原点b=0)
从上述对超平面和半空间集合表达式定义形式很难直观的感受定义与性质,下面我们通过在二维平面中的例子来理解一下超平面与半空间的几何意义,如下图所示:
- 红色直线(不过原点)称之为一个二维平面上的超平面,具有直线集合所有的性质,属于仿射集、凸集;
- 蓝色直线(过原点)为红色直线的特例,除了是仿射集/凸集之外,还是个凸锥;
- 红色直线把二维平面分成了1和2两个空间,这两个空间称为半空间,并且满足凸集的定义,因此是半空间是凸集;
- 与超平面一样,当超平面过原点时,半空间也满足凸锥的定义,此时半空间也是个凸锥;

2.2 球和椭球
同样以二维平面上的圆和椭圆去理解比较容易理解,这里就不做赘述,只给出简单定义:
球
定义:
B ( x c , r ) = { x ∣ ∥ x − x c ∥ 2 ≤ r } = { x ∣ ( x − x c ) T ( x − x c ) ≤ r } B(x_c,r)=\{x\:|\parallel x-x_c \parallel _2 \:\le r\}=\{x\:|\sqrt{(x-x_c)^T(x-x_c)}\le r\} B(xc,r)={x∣∥x−xc∥2≤r}={x∣(x−xc)T(x−xc)≤r}
性质: 凸集 仿射集(r=0) 凸锥(r=0 & 原点)
椭球:
定义: (对称正定矩阵几何)
ξ ( x c , P ) = { x ∣ ( x − x c T ) P − 1 ( x − x c ) ≤ 1 } x c ∈ R n P ∈ S + + n \xi(x_c,P)=\{x\:| (x-x_c^T)P^{-1}(x-x_c) \:\le 1\} \: x_c\in R^n \: P\in S_{++}^{n} ξ(xc,P)={x∣(x−xcT)P−1(x−xc)≤1}xc∈RnP∈S++n
性质: 凸集
假设: P = r 2 I n P=r^2I_n P=r2In, r ≠ 0 r\neq0 r=0 奇异值大于0
A矩阵 A T A A^TA ATA 特征值: e i g ( A T A ) ≥ 0 eig(A^TA) \ge0 eig(ATA)≥0 奇异值: e i g ( A T A ) \sqrt{eig(A^TA)} eig(ATA)
P P P 奇异值对应椭球半轴长
例子:
ξ = { x ∣ x T ( 4 0 0 1 ) − 1 x ≤ 1 } = { ( x 1 , x 2 ) ∣ 1 4 x 1 2 + x 2 2 ≤ 1 } \begin{aligned} \xi &=\{x\:| x^T\begin{pmatrix} 4 & 0\\ 0 & 1 \end{pmatrix}^{-1}x \:\le 1\}\\ &=\{(x_1,x_2)|\frac{1}{4}x_1^2+x_2^2 \le 1\} \end{aligned} ξ={x∣xT(4001)−1x≤1}={(x1,x2)∣41x12+x22≤1}
2.3 多面体(关注单纯形)
多面体:可以简单的理解为超平面与半空间的交集,数学表达式如下:
P = { x ∣ a j T x ≤ b j i = 1 ⋯ m c j T x = d j i = 1 ⋯ m } P=\Bigg\{x\:\mid \begin{aligned} a_j^Tx \le b_j\qquad i=1\cdots m\\ c_j^Tx = d_j \qquad i=1\cdots m\\ \end{aligned}\Bigg\} P={x∣ajTx≤bji=1⋯mcjTx=dji=1⋯m}
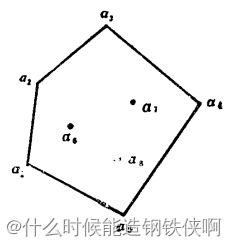
其中有界多面体为凸集 ,如下图中集合P(阴影部分:由五条直线与其分割形成的相应半空间的交集)所示:

单纯形定义:
R n R^n Rn空间中选择 v 0 ⋯ v k v_0\cdots v_k v0⋯vk共 k + 1 k+1 k+1个点, v 1 − v 0 , ⋯ , v k − v 0 v_1-v_0,\cdots,v_k-v_0 v1−v0,⋯,vk−v0线性无关,则与上述点相关的单纯形为:
C = C o n v { v 0 ⋯ v k } = { θ 0 v 0 + θ 1 v 1 + θ 2 v 2 + ⋯ + θ k v k ∣ θ 0 ⋯ θ k ≥ 0 , θ 0 + ⋯ + θ k = 1 } C=Conv\{v_0\cdots v_k\}=\{\theta_0v_0+\theta_1v_1 + \theta_2v_2 + \cdots + \theta_kv_k \:|\: \theta_0 \cdots \theta_k \ge 0,\:\theta_0 +\cdots +\theta_k = 1 \} C=Conv{v0⋯vk}={θ0v0+θ1v1+θ2v2+⋯+θkvk∣θ0⋯θk≥0,θ0+⋯+θk=1}
例子:
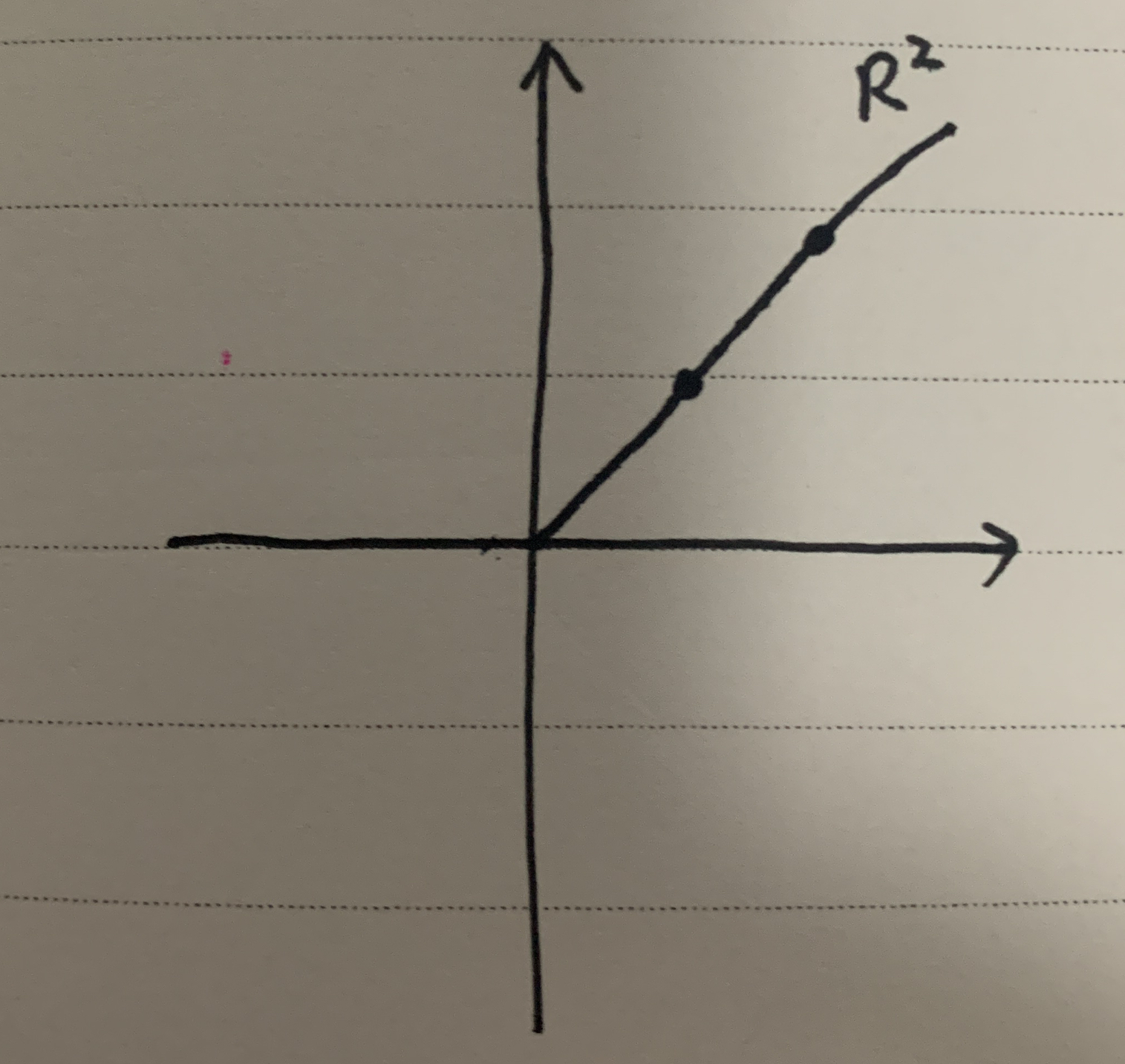
- R R R 一维空间, 两个点单纯形为两点连接线段,
- R 2 R^2 R2 二维空间, 两个点单纯形为两点连接线段, 三个点为两个向量围成的三角形, 四个点无法满足线性无关的三个向量
- R 3 R^3 R3 三维空间,四个点单纯形为一个四面体
证明:单纯形是多面体的一种
x ∈ C ∈ R n x\in C \in R^n x∈C∈Rn C C C为单纯形 x x x ⇔ \Leftrightarrow ⇔ θ 0 v 0 + θ 1 v 1 + θ 2 v 2 + ⋯ + θ k v k \theta_0v_0 + \theta_1v_1 + \theta_2v_2 + \cdots + \theta_kv_k θ0v0+θ1v1+θ2v2+⋯+θkvk
θ 0 ⋯ θ k ≥ 0 , θ 0 + ⋯ + θ k = 1 \theta_0 \cdots \theta_k \ge 0,\:\theta_0 +\cdots +\theta_k = 1 θ0⋯θk≥0,θ0+⋯+θk=1. v 1 − v 0 , ⋯ , v k − v 0 v_1-v_0,\cdots,v_k-v_0 v1−v0,⋯,vk−v0线性无关
首先定义下面两个向量:
[ θ 1 ⋯ θ k ] T = y [\theta_1 \cdots \theta_k]^T=y [θ1⋯θk]T=y, y ≥ 0 y\ge0 y≥0, 1 T y ≤ 1 1^Ty\le1 1Ty≤1,
[ v 1 − v 0 , ⋯ , v k − v 0 ] = B ∈ R n × k [v_1-v_0, \cdots, v_k-v_0]=B\in R^{n\times k} [v1−v0,⋯,vk−v0]=B∈Rn×k
因此:
X ∈ C ⇔ X = θ 0 v 0 + θ 1 v 1 + θ 2 v 2 + ⋯ + θ k v k = v 0 + θ 1 ( v 1 − v 0 ) + ⋯ + θ k ( v k − v 0 ) = v 0 + B y \begin{aligned} X \in C \Leftrightarrow X &=\theta_0v_0 + \theta_1v_1 + \theta_2v_2 + \cdots + \theta_kv_k\\ &= v_0 + \theta_1(v_1-v_0)+ \cdots + \theta_k(v_k-v_0) \\ &= v_0 +By\\ \end{aligned} X∈C⇔X=θ0v0+θ1v1+θ2v2+⋯+θkvk=v0+θ1(v1−v0)+⋯+θk(vk−v0)=v0+By
B包含k个线性无关的向量,因此: r a n k ( B ) = k ( k ≤ n ) rank(B)=k \quad (k \le n) rank(B)=k(k≤n)
B是列满秩矩阵,可以转换成: [ I k 0 ] \begin{bmatrix} I_k \\[0.3em] 0\end{bmatrix} [Ik0]
存在一个非奇异矩阵 A = [ A 1 A 2 ] ∈ R n × n A=\begin{bmatrix}A_1 \\[0.3em] A_2\end{bmatrix} \in R^{n \times n} A=[A1A2]∈Rn×n使得 A B = [ A 1 A 2 ] B = [ I k 0 ] AB=\begin{bmatrix}A_1 \\[0.3em] A_2\end{bmatrix}B =\begin{bmatrix} I_k \\[0.3em] 0\end{bmatrix} AB=[A1A2]B=[Ik0]
由 X = v 0 + B y X=v_0+By X=v0+By 左右两边同乘以 A A A 的:
A X = A v 0 + A B y AX =Av_0+ABy AX=Av0+ABy ⇔ \Leftrightarrow ⇔ [ A 1 A 2 ] X = [ A 1 A 2 ] v 0 + [ A 1 B A 2 B ] y \begin{bmatrix}A_1 \\[0.3em] A_2\end{bmatrix}X=\begin{bmatrix}A_1 \\[0.3em] A_2\end{bmatrix}v_0+\begin{bmatrix}A_1B \\[0.3em] A_2B \end{bmatrix}y [A1A2]X=[A1A2]v0+[A1BA2B]y ⇔ \Leftrightarrow ⇔ { A 1 X = A 1 v 0 + y A 2 X = A 2 v 0 \begin{cases} A_1X=A_1v_0+y \\ A_2X=A_2v_0 \\ \end{cases} {A1X=A1v0+yA2X=A2v0
⇔ \Leftrightarrow ⇔ { A 1 X ≥ A 1 v 0 1 T A 1 X ≤ 1 + 1 T A 1 v 0 A 2 X = A 2 v 0 \begin{cases} A_1X &\ge A_1v_0 \\ 1^TA_1X &\le 1+ 1^TA_1v_0 \\ A_2X &=A_2v_0 \\ \end{cases} ⎩⎪⎨⎪⎧A1X1TA1XA2X≥A1v0≤1+1TA1v0=A2v0
两个线性不等式和一个线性等式=多面体
2.4 半正定锥
对称矩阵集合 S n = { X ∈ R n × n ∣ X = X T } S^n=\{X\in R^{n\times n}|X=X^T\} Sn={X∈Rn×n∣X=XT} 凸集 凸锥
对称半正定矩阵集合 S + n = { X ∈ R n × n ∣ X = X T , X ⪰ 0 } S_{+}^n=\{X\in R^{n\times n}|X=X^T,\: X \succeq 0\} S+n={X∈Rn×n∣X=XT,X⪰0} 其中 X ⪰ 0 X \succeq 0 X⪰0表示特征值大于等于0 凸集 凸锥
对称正定矩阵集合 S + + n = { X ∈ R n × n ∣ X = X T , X ≻ 0 } S_{++}^n=\{X\in R^{n\times n}|X=X^T,\: X \succ 0\} S++n={X∈Rn×n∣X=XT,X≻0} 其中 X ≻ 0 X \succ 0 X≻0表示 X X X是正定矩阵 凸集 非凸锥
证明 S + n S_{+}^n S+n 是凸集、凸锥
∀ θ 1 , θ 2 ≥ 0 \forall \theta_1, \: \theta_2 \: \ge 0 ∀θ1,θ2≥0 ∀ A , B ∈ S + n \forall \: A, \: B \in S_{+}^n ∀A,B∈S+n 证明 θ 1 A + θ 2 B ∈ S + n \theta_1A+\theta_2B \in S_+^n θ1A+θ2B∈S+n 即证明 θ 1 A + θ 2 B \theta_1A+\theta_2B θ1A+θ2B 对称半正定
如果 A , B A, B A,B是半正定矩阵,则对于 ∀ X ∈ R n \forall X\in R^n ∀X∈Rn, X T A X ≥ 0 X T B X ≥ 0 \begin{aligned} X^TAX &\ge 0 \\ X^TBX &\ge 0 \\ \end{aligned} XTAXXTBX≥0≥0
由上可知证明半正定即证明 X T ( θ 1 A + θ 2 B ) X ≥ 0 = X T θ 1 A X + X T θ 2 B X ≥ 0 X^T(\theta_1A+\theta_2B)X \ge 0=X^T \theta_1AX+X^T \theta_2BX \ge 0 XT(θ1A+θ2B)X≥0=XTθ1AX+XTθ2BX≥0
因此得证
考虑简单情况:
当 n = 1 n=1 n=1 时, S + n = R + S_+^n=R_+ S+n=R+ S + + n = R + + S_{++}^n=R_{++} S++n=R++ S n = R S^n=R Sn=R 可知对称正定矩阵 S + + n S_{++}^n S++n不包含原点,因此非凸锥
S + n S_+^n S+n n = 2 n=2 n=2 S + n = { [ x y y z ] ∣ x ≥ 0 , z ≥ 0 , x z ≥ y 2 } S_+^n=\Bigg\{\begin{bmatrix} x&y \\[0.3em] y&z\end{bmatrix} | x \ge 0,\:z\ge0,\: xz\ge y^2 \Bigg\} S+n={[xyyz]∣x≥0,z≥0,xz≥y2} 二维矩阵空间与xyz 三维空间可以对应起来, 如下图所示:
交集
若 S 1 , S 2 S_1,S_2 S1,S2为凸集,则 S 1 ⋂ S 2 S_1 \bigcap S_2 S1⋂S2为凸
若 S a S_a Sa为凸集, ∀ a ∈ A \forall a\in A ∀a∈A 则 ⋂ a ∈ A S a \mathop{\bigcap} \limits_{a\in A} S_a a∈A⋂Sa为凸集

2.5参考
1、Stephen Boyd 、Lieven Vandenberghe——《Convex Optimization》)
2、中科大凌青凸优化 (https://www.bilibili.com/video/BV1Jt411p7jE?)