通过查阅相关资料发现动态规划问题一般就是求解最值问题。这种方法在解决一些问题时应用比较多，比如求最长递增子序列等。

有部分人认为动态规划的核心就是：穷举。因为要求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值。

首先，笔者认为动态规划中的穷举有一定的特点，因为这类问题有重叠的子问题存在，暴力穷举效率极其低下，所以需要“备忘录（DP Table）”优化穷举过程，从而尽可能的避免不必要的计算。其次，动态规划问题一定有“最优子结构”，只有这样才能通过子问题的最值得到原问题的最值。另外，穷举所有可行解通常较为困难，只有列出正确的“状态转移方程”才能正确地穷举。

上述的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。在实际应用中写出状态转移方程是最困难的。通常根据 “明确问题状态 -> 定义 dp 数组/函数的具体含义 -> 明确转移 -> 明确基本实例” 来构建状态转移方程。

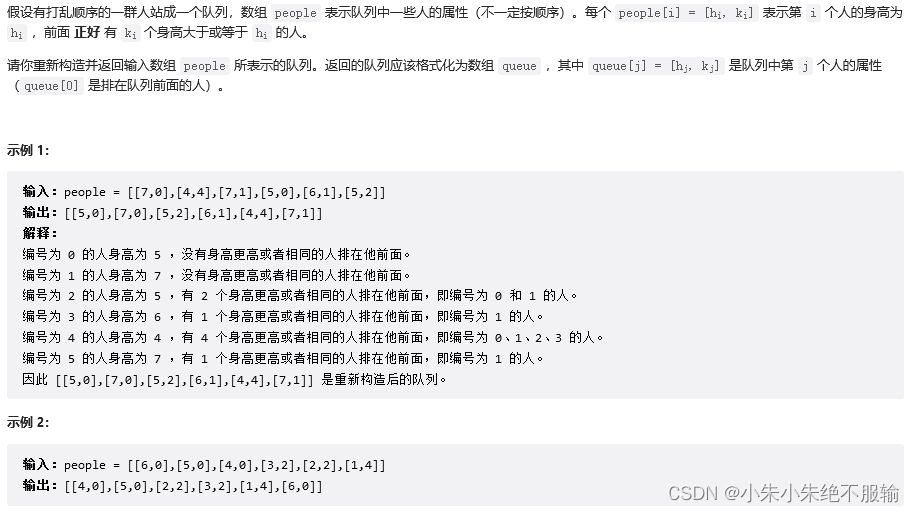
最长递增子序列 LeetCode#300

dp[i] 表示当最后一个数值为 nums[i] 时，此时对应的最长递增子序列的长度是 dp[i]。在下述例子中当 i=2 时 dp[2] 表示当最后一个数为 3 时，对于数组 {1, 4, 3} 中最长递增子序列的长度 dp[2]=2。

基于动态规划理论，当已知前面第 i - 1 个值时，可以利用下述代码求解得到第 i 个值。

for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) {dp[i] = max(dp[i], dp[j] + 1);}
}

当得到 dp 数组后，只需要求得 dp 数组的最大值（即为最大递增子序列的长度）即可。

int ret = 1;
for (auto it : dp) {ret = max(ret, it);
}

普通动态规划算法 O(N^2)

因此可以利用该方法解决 #300 问题，具体代码如下所示。但是该算法的时间复杂度为 O(n^2)，这对于较大数据量而言，性能不太能接受。

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int length = nums.size();vector<int> dp(length, 1);for (int i = 0; i < length; i++) {//对于某一个还未计算的dp[i]，在nums的前i个中找到比nums[i]小的dp[j]，//然后进行加1；可能会出现多个满足的dp[j]，取其中值最大的一个作为最终结果。for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) {dp[i] = max(dp[i], dp[j] + 1);}}}//找到dp数组中的最大值（也就是最长递增子序列的长度）int ret = 1;for (auto it : dp) {ret = max(ret, it);}return ret;}
};

优化动态规划算法 O(NlogN)

对于该方法的具体优化可以参考 动态规划设计之最长递增子序列

该算法的思路有点像游戏 “空当接龙”，也就是对于每一张扑克牌，数值小的牌只能放在大牌的堆上面，当没有合适的堆时，新建一个堆放置该扑克牌；当有多个满足条件的堆时，将扑克牌放在最左端的堆上面（保证扑克牌堆顶的牌有序）。

#define MAX_HEAP 2500
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int heap_top_num[MAX_HEAP];int heap_cnt = 0;for (auto num : nums) {int left = 0;//对于每一个 num，区间右边的值需要重新设置初始值。int right = heap_cnt;while (left < right) {int mid = (left + right) >> 1;//找到最先大于 num 的堆定元素if (heap_top_num[mid] >= num) {right = mid;}else {left = mid + 1;}}//当没有找到符合条件的 mid 时，退出条件是最右端区间位置，也就是 heap_cnt。//此时需要新建一个数值堆if (left == heap_cnt) {heap_cnt++;}heap_top_num[left] = num;}//堆的个数就是最长递增子序列的长度return heap_cnt;}
};

转变最长递增子序列应用 LeetCode#354

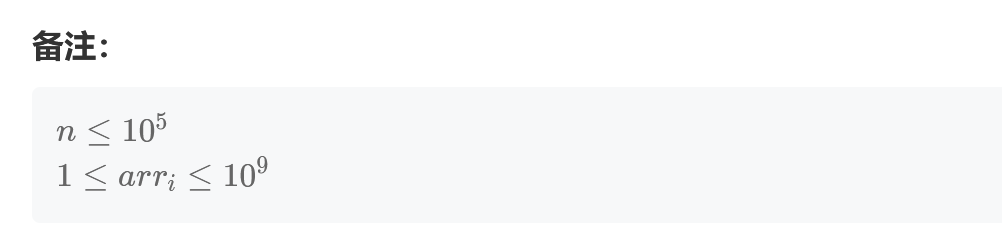
这道题目需要按照第一维参数进行升序排序，然后按照第二维参数降序排序（该维度中找出最长递增子序列即可）。

注意点对于二维的 vector<vector<int>> 按照用户自定义排序方式进行排序。

首先按照第一维度进行升序排序，如果第一维度元素相等，则按照第二维度进行降序排序。这里平时写的重载的逻辑有所不一致，需要特别注意。

sort(envelopes.begin(), envelopes.end(), [](const vector<int>& a, const vector<int>& b) {return a[0] == b[0] ? a[1] > b[1]: a[0] < b[0];});

#define MAX_EN 100002
class Solution {
public:int heap_top[MAX_EN];int max_evlp;//利用二分法求解最长递增子序列的长度。int longIncSub(vector<vector<int>>& sorted_subs) {for (int i = 0; i < max_evlp; i++) {heap_top[i] = 1;}int sub_cnt = 0;for (const auto& evlp : sorted_subs) {int left = 0;int right = sub_cnt;while (left < right) {int mid = (left + right) >> 1;if (heap_top[mid] >= evlp[1]) {right = mid;}else {left = mid + 1;}}if (left == sub_cnt) {sub_cnt++;}heap_top[left] = evlp[1];}return sub_cnt;}int maxEnvelopes(vector<vector<int>>& envelopes) {max_evlp = envelopes.size();//对二维vector按照用户需要的排序规则进行排序方法。sort(envelopes.begin(), envelopes.end(), [](const vector<int>& a, const vector<int>& b) {return a[0] == b[0] ? a[1] > b[1]: a[0] < b[0];});return longIncSub(envelopes);}
};