题目：

给定数组arr，设长度为n，输出arr的最长递增子序列。（如果有多个答案，请输出其中字典序最小的）

输入描述:

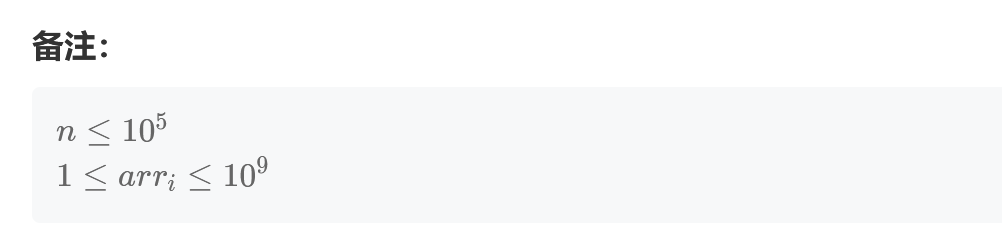
输出两行，第一行包括一个正整数n（n<=100000），代表数组长度。第二行包括n个整数，代表数组arr 。 (1 ≤ arr[i] ≤ 1e9)

输出描述:

输出一行。代表你求出的最长的递增子序列。

示例1

输入

9 2 1 5 3 6 4 8 9 7

输出

1 3 4 8 9

示例2

输入

5 1 2 8 6 4

输出

1 2 4

说明

其最长递增子序列有3个，（1，2，8）、（1，2，6）、（1，2，4）其中第三个字典序最小，故答案为（1，2，4）

备注:

时间复杂度O(NlogN)，空间复杂度O(N)。

思路分析：

由递增子序列，可以知道该序列是依赖与前面序列，且连续性要求较高
1. 所以dp[i]存储的值是以array[i]元素结尾时的最优解，即最长递增子序列
dp[i]点最长子序列依赖于所有array[小于i的值]的dp[]值中的最大值
1. 比如array = {1,3,5,4,6,5,7}
2. dp[]的前三位是{1,2,3} 则第dp[3]，
3. 查到array[0]
4. 而dp[1]>dp[0] 所以将dp[3]赋值为dp[1]+1,因为前三位中有个长度为2的序列的结尾数比array[3]小
依次更新dp,找到dp的最大值，即为最长递增子序列的长度

改进：

每次求dp都要遍历一次array的前面部分，导致时间复杂度时O(N^2)
但是之前的array与dp已经遍历过了，现在我们要做的是将其中重要的信息存储起来
1. 重要信息:长度为0/1/2/3的子序列，最小要以什么array结尾
2. 每次dp的更新就不需要去遍历所有array，
  1. 需要查找到合适的结尾数，在其基础上将序列长度加一。并根据当前dp，array更新“重要信息”
3. 序列长度，与结尾数的映射一定是单调递增的，所以，查找时，可以用二分查找，或者用有序表来组织（ceilingKey()方法）

得到最长子序列：

根据dp，dp存储的是以dp[i]结尾时的最长子序列长度，
那么倒序遍历dp，当dp[i]的值等于len,len-1,len-2....时说明是最长子序列的最小字典序

易错点：

在用有序表TreeMap时，如果要将（键1，值1）替换成（键2，值1)，不能单纯使用replace，put方法，要先remove（键1，值1），再put(键2，值1)

代码展示：

import java.io.*;
import java.util.TreeMap;public class Main{public static void main(String[] args)throws IOException{BufferedReader read = new BufferedReader(new InputStreamReader(System.in));int n = Integer.parseInt(read.readLine());String[] str = read.readLine().split(" ");int dp[] = new int[n];//以array[i]结尾的序列的最长长度int array[] = new int[n];for(int i=0;i<n;i++){array[i] = Integer.parseInt(str[i]);dp[i] = 0;}int max = 0;//最长子序列长度int flag = 0;//当前最长序列TreeMap<Integer,Integer> map = new  TreeMap<Integer,Integer>();//（长度为i的最小结尾数, 序列长度i)for(int i=0;i<n;i++){Integer key = map.ceilingKey(array[i]);if(key == null){//没找到ceiling，说明当前array是最大的，添加一个键值对，序列长度加1map.put(array[i],++flag);dp[i] = flag;}else{//找了，更新，（键1，值1）替换成（键2，值1)dp[i] = map.get(key);map.remove(key);map.put(array[i],dp[i]);}max = Math.max(max, dp[i]);}//System.out.println(max);String sout = "";for(int j = n-1;j>=0;j--){//倒序遍历，遇到len,len-1,len-1...将其加入字符串if(dp[j] == max){sout =  array[j]+" "+sout ;max--;}}System.out.print(sout);}
}