目录

一.最长递增子序列问题I

二.最长递增子序列问题II

三. 最长递增子序列问题III

---

一.最长递增子序列问题I

1.对应牛客网链接

最长上升子序列(一)_牛客题霸_牛客网 (nowcoder.com)

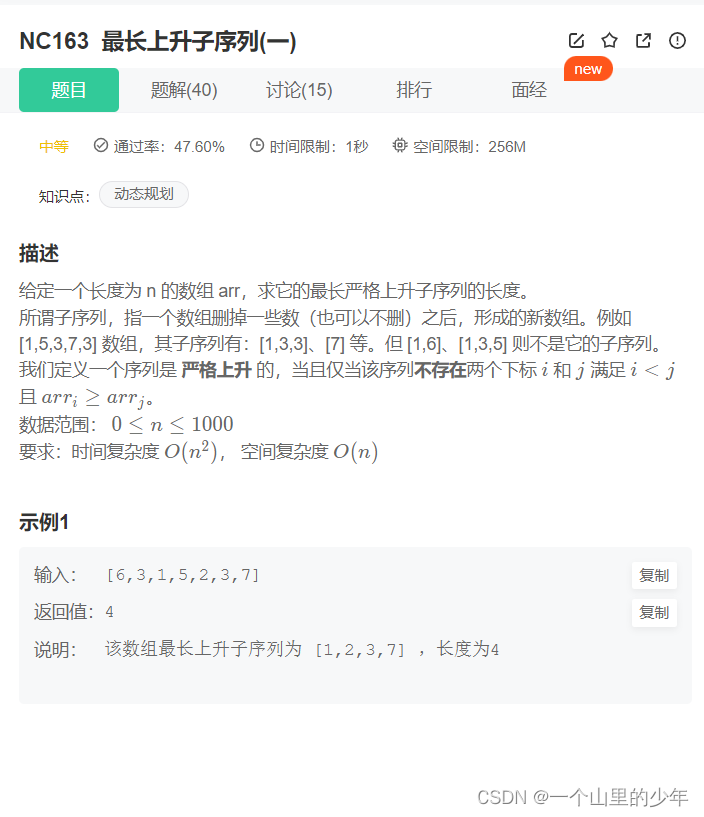
2.题目描述：

 3.解题思路

1.首先我们分析题意：最长递增子序列拆：要递增的，还是序列，不一定连续 ，要长度最长的。

2.子序列和子数组问题我们一般考虑必须以某个位置结尾如何如何，在本题中我们可以这样考虑必须以i位置结尾的情况下最长递增子序列的最大长度是多少我们每个位置都这么干那么答案一定就在其中

下面以[5,7,1,9,4,6,2,8,3]为例：

第一个元素 5： 递增长度只能为1， 接下来第二个7，比5大，长度为2

 

第三个元素 1：前面没有比它大的，只能为1 ， 第四个元素9，前面有5，7，故长度为3到这里你发现，9比7大，7往前构成的长度是2，那9就可以接在7的后面，变成长度加一的新序列。

 我相信老铁应该懂了

4.对应代码：

class Solution {public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** 给定数组的最长严格上升子序列的长度。* @param arr int整型vector 给定的数组* @return int整型*/int LIS(vector<int>& arr) {if (arr.empty())return 0;// write code hereint N = arr.size();vector<int>dp(N, 1);//每个位置最长递增子序列的长度至少为1自己本身就是//dp的含义是必须以i位置结尾的情况下最长递增子序列的最大长度int maxLen = 1;for (int i = 1; i < N; i++) {for (int j = 0; j < i; j++) {if (arr[i] > arr[j]) {dp[i] = max(dp[i], dp[j] + 1); //长度加1}}maxLen = max(maxLen, dp[i]);//更新最大长度}return maxLen;}};

二.最长递增子序列问题II

1.对应牛客网链接：

最长上升子序列(二)_牛客题霸_牛客网 (nowcoder.com)

2.题目描述：

 3.解题思路：

1.在这里我们引入end数组，end[i]的值为最目前为止长度为i+1的最小结尾

2.每次去end数组里面去找大于等于arr[i]最左的位置

 

我们看同样是长度为2的子序列，[2,3]就比[2,5]好。因为[2,3]后面如果有4的话，组成[2,3,4]长度就是3了，但是[2,5]因为不满足条件，就没法组队了。

我们组成子序列的时候，不仅要让这个序列尽可能的长，而且要让子序列中的上升的时候尽可能的缓慢，[2,3]就比[2,5]上升的缓慢，这样就有机会能拼接出更长的上升子序列。我们用一个数组来保存当前的最长上升子序列，这个数组是严格递增的。
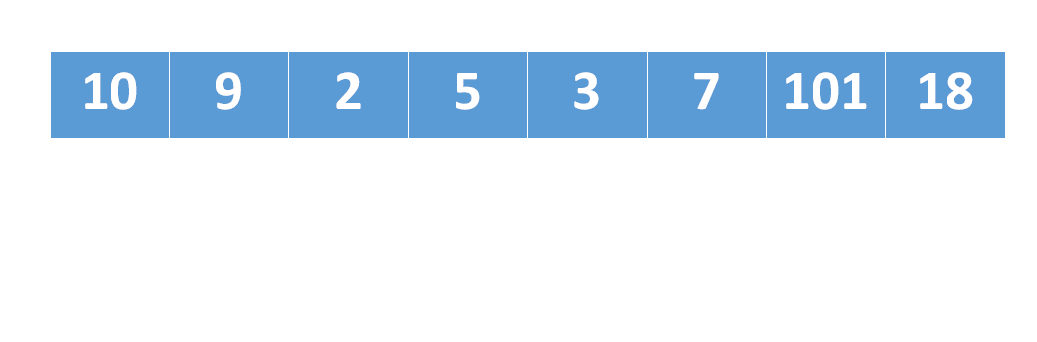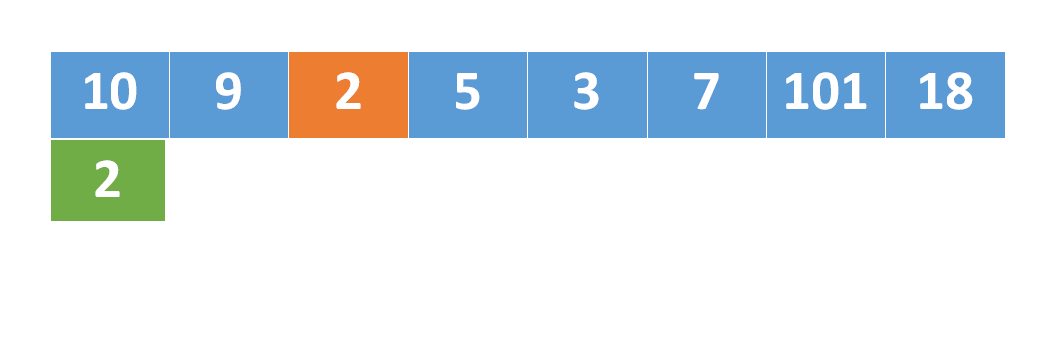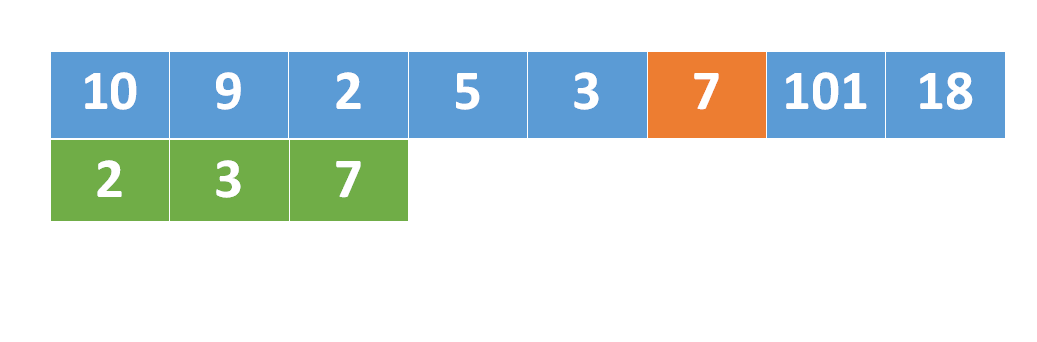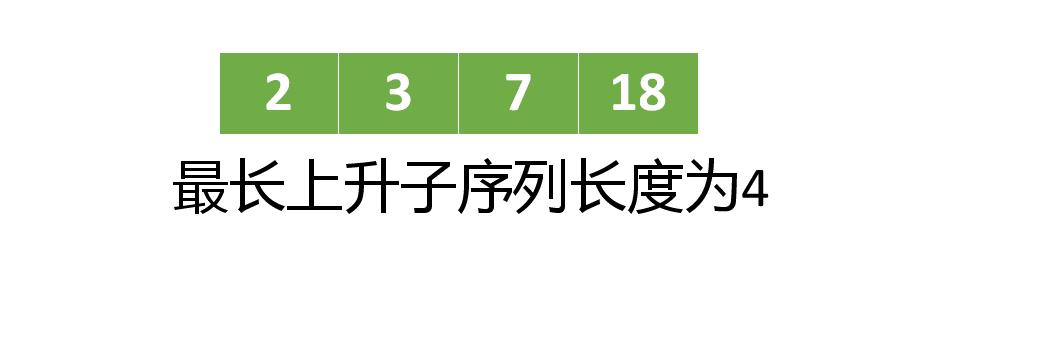
因为是严格递增的，数组中最后一个值nums[max]就是最大值，如果下次再碰到一个数字n，它比num[max]还要大，那么很明显，这个子序列的长度就要+1，并且将数组n添加到数组的末尾。

[2,3,7,8,11,13,18]是目前为止最长的上升子序列，之后如果又碰到了19，或者101，因为他们都大于数组中的最大值18，所以直接将其添加到数组末尾就可以了，同时子序列的长度要+1。19和101的例子很好理解，但如果下次碰到的数字是6或者12呢？因为要让子序列上升的尽可能缓慢，那么让[2,5,7...]变成[2,5,6...]更合适，因为后者上升的更缓慢。同样,将[...8,11,13,18]变成[...8,11,12,18]也是上升的更缓慢一点。
也就是，已知上升子序列[i,i_1,i_2,....,i_n]，现在我们在继续遍历的过程中碰到了一个值i_k，这个值是小于i_n的，所以上升子序列的长度还是不变。但是我们需要找到一个位置，将i_k替换掉某个旧的值。

对应动图：

4.对应代码：

class Solution {public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** 该数组最长严格上升子序列的长度* @param a int整型vector 给定的数组* @return int整型*/int LIS(vector<int>& arr) {// write code hereif (arr.empty()) {return 0;}int N = arr.size();vector<int>end(N);//end[i]的含义是目前为止长度为i+1的最小结尾end[0] = arr[0];int L = 0;int maxLen = 1;int right = 0; //用于控制end数组的范围int R = right;for (int i = 1; i < N; i++) {L = 0;R = right;while (L <= R) {//用于查找大于等于arr[i]最左边的位置int mid = (L + R) >> 1;if (arr[i] > end[mid]) {L = mid + 1;} else {R = mid - 1;}}right = max(right, L); //更新右边界maxLen = max(maxLen, L + 1);end[L] = arr[i];}return maxLen;}
};

三. 最长递增子序列问题III

1.对应letecode链接：

最长上升子序列(三)_牛客题霸_牛客网 (nowcoder.com)

2.题目描述：

3.解题思路

1.本题只是上题的一个升级版我们只需要定义一个变量记录 一下最长递增子序列的结尾位置在哪里即可，然后再依次遍历

4.对应代码：

class Solution {public:/*** retrun the longest increasing subsequence* @param arr int整型vector the array* @return int整型vector*/vector<int> LIS(vector<int>& arr) {// write code hereif (arr.empty()) {return {};}int N = arr.size();vector<int>dp(N, 1);vector<int>end(N);int maxLen = 1;int maxIndex = 0;end[0] = arr[0];int right = 0;int L = 0;int R = right;for (int i = 1; i < N; i++) {L = 0;R = right;while (L <= R) {int mid = (L + R) >> 1;if (arr[i] > end[mid]) {L = mid + 1;} else {R = mid - 1;}}right = max(right, L);maxLen = max(maxLen, L + 1);end[L] = arr[i];dp[i] = L + 1;if (dp[i] >= maxLen) {//由于要求子典序最小maxIndex = i;maxLen = dp[i];}}vector<int>ans(maxLen);//获取最长的递增子序列for (int i = maxIndex; i >= 0; i--) {if (dp[i] == maxLen) {ans[--maxLen] = arr[i];}}return ans;}
};

思考题：如果要获取所有递增子序列了？

#include<iostream>
#include<vector>
using namespace std;
vector<int> process(vector<int>& arr,vector<int>&dp ,int maxLen, int index) {//获取所有最长递增子序列vector<int>ans(maxLen);for (int i = index; i >= 0; i--) {if (dp[i] == maxLen) {ans[--maxLen] = arr[i];}}cout << "进来" << endl;return ans;}
int main() {int N;cin >> N;vector<int>arr(N);for (int i = 0; i < N; i++) {cin >> arr[i];}vector<int>dp(N, 1);vector<int>end(N);int maxLen = 1;int maxIndex = 0;end[0] = arr[0];int right = 0;int L = 0;int R = right;for (int i = 1; i < N; i++) {L = 0;R = right;while (L <= R) {int mid = (L + R) >> 1;if (arr[i] > end[mid]) {L = mid + 1;}else {R = mid - 1;}}right = max(right, L);maxLen = max(maxLen, L + 1);end[L] = arr[i];dp[i] = L + 1;if (dp[i] >= maxLen) {maxIndex = i;maxLen = dp[i];}}vector<vector<int>>ans;for (int i = 0; i < N; i++) {if (dp[i] == maxLen) {ans.push_back(process(arr, dp, maxLen, i));}}for (int i = 0; i < ans.size(); i++) {for (int j = 0; j < ans[0].size(); j++) {cout << ans[i][j] << " ";}cout << endl;}return 0;
}