NC91 最长递增子序列
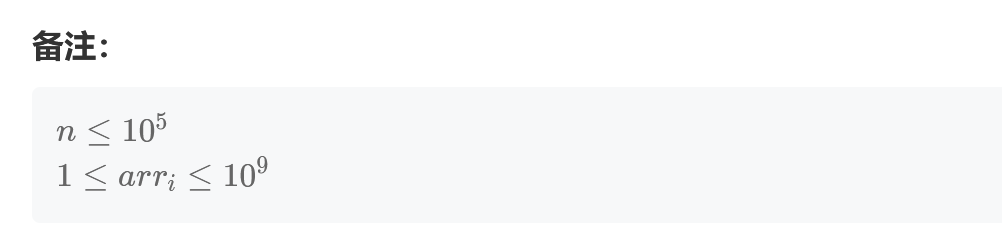这道题n的范围是1e5，因此不能使用常规的dp[i]，表示以i结尾的最大的子序列，因为这个时间复杂度是n方级别。因此要换一种算法。

贪心+二分，时间复杂度为O(nlogn)

下面说说贪心+二分的解法，举例说明基本思路，假设数组arr为[2, 3, 1, 2, 3]，vec数组里面存放递增子序列，maxLen数组里存放以元素i结尾的最大递增子序列长度，那么遍历数组arr并执行如下更新规则:

初始情况下，vec为[2]，maxLen[1]
接下来遇到3，由于vec最后一个元素小于3，直接更新，vec为[2,3]，maxLen[1,2]
接下来遇到1，由于vec最后的元素大于1, 我们在vec中查找大于等于1的第一个元素的下标，并用1替换之，此时vec为[1,3], maxLen[1,2,1]
接下来遇到2，由于vec最后的元素大于2，我们在vec中查找大于等于2的第一个元素的下标，并用2替换之，此时vec为[1,2], maxLen[1,2,1,2]
接下来遇到3，由于vec最后一个元素小于3，直接更新，vec为[1,2,3]，maxLen为[1,2,1,2,3]
此时vec的大小就是整个序列中最长递增子序列的长度（但是vec不一定是本题的最终解） 

假设我们原始数组是arr1，得到的maxLen为[1,2,3,1,3]，最终输出结果为res（字典序最小的最长递增子序列），res的最后一个元素在arr1中位置无庸置疑是maxLen[i]==3对应的下标，那么到底是arr1[2]还是arr1[4]呢？如果是arr1[2]，那么arr1[2]<arr1[4]，则maxLen[4]==4，与已知条件相悖。因此我们应该取arr1[4]放在res的最后一个位置。

上代码：

class Solution {
public:vector<int> LIS(vector<int>& arr) {// write code herevector<int> vec;vector<int> Maxn;if(arr.size()==0) return vec;vec.push_back(arr[0]);Maxn.push_back(1);for(int i=1;i<arr.size();i++){if(arr[i]>vec[vec.size()-1]){vec.push_back(arr[i]);Maxn.push_back(vec.size());}else {int pos=lower_bound(vec.begin(),vec.end(),arr[i])-vec.begin();vec[pos]=arr[i];Maxn.push_back(pos+1);}}int len=vec.size();vector<int > v;for(int i=arr.size()-1;i>=0;i--){if(Maxn[i]==len){len--;v.push_back(arr[i]);}}reverse(v.begin(), v.end());return v;}
};