一、下面是原题描述

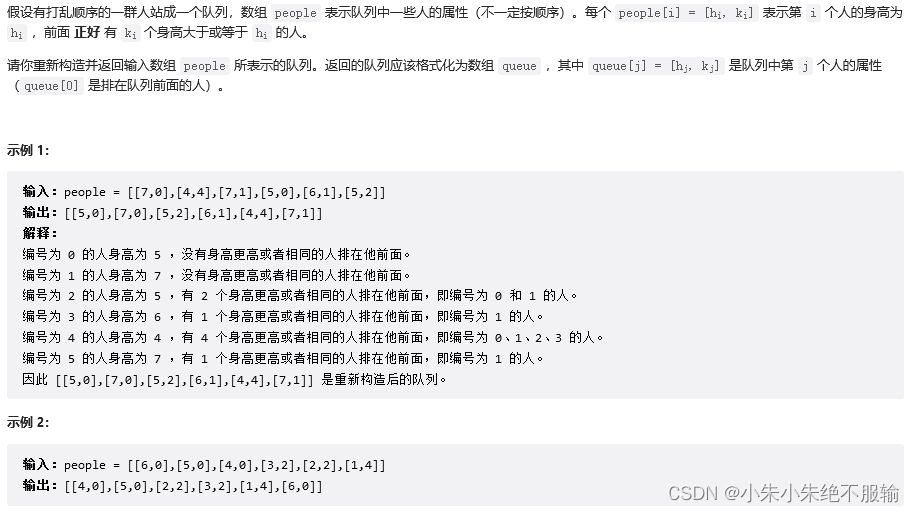
给定一个未排序的整数数组，找到最长递增子序列的个数。

示例 1:

输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
示例 2:

输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1，并且存在5个子序列的长度为1，因此输出5。
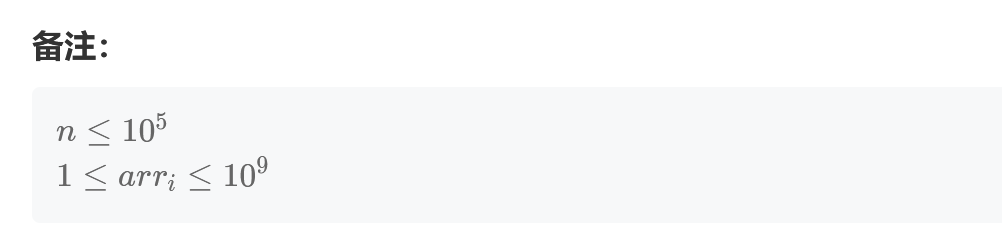
注意: 给定的数组长度不超过 2000 并且结果一定是32位有符号整数。

1.1题目分析

由于上一篇博客已经分析过求最长上升子序列长度——C++的经典LIS问题，该题是求最长增长子序列个数，经过分析，这题也只是经典LIS(Longest Increasing Subsequence)问题的变种，也就是用同样的LIS框架，区别在于本体需要额外记录每个最长子序列个数。下面是具体实现思路。

用dp[i]记录最长子序列长度maxLen，count[i]记录最长子序列个数，其中i表示数组的元素个数，0 <= i < n；如果求出前dp[i]和count[i]的i-1元素的值，则可以推导出：

dp[i] = max(dp[j]) + 1，满足条件nums[i] > nums[j]，0 =< i < n，0 <= j < i - 1；

当nums[i] > nums[j]时，有：

如果dp[i] == dp[j] + 1，则count[i] += count[j]；
如果dp[i] < dp[j] + 1，则count[i] = count[j]；

第(1.)需要累加是因为前面遇到一个相同的最长子序列，需要把该子序列也加上。后面第(2.)之所以重新赋值，是因为第一次遇到更长的子序列，故需要更新count[i]最长子序列长度。

当求出全部的count[i]后，需要遍历找出等于maxLen的所有count[j]，然后将这些满足条件的coount[j]全部相加即为最长子序列长度asn。

动态规划满足三个条件：状态方程、状态转移方程、边界条件，根据分析可知该题满足条件，下面是分析的表格：

nums = {10, 9, 2, 5, 3, 7, 101, 18}

dp[i] = max(dp[j]) + 1，满足条件nums[i] > nums[j]，0 =< i < n，0 <= j < i - 1；

当nums[i] > nums[j]时，有：

如果dp[i] == dp[j] + 1，则count[i] += count[j]；
如果dp[i] < dp[j] + 1，则count[i] = count[j]；

元素下标n 0 1 2 3 4 5 6 7
元素值 10 9 2 5 3 7 101 18
dp[i](或LIS) 1 1 1 2 2 3 4 4
count 1 2 3 1 2 2 2 4

1.2代码实现分析

1.2.1求出dp[i]和count[i]的值

假如nums[i]>nums[j]，则更新dp[i]和count[i]，更新规则为假如dp[i]<dp[j]+1，dp[i]=dp[j]+1，且count[i]=count[j]，着两条语句是假如有更长最长子序列，则更新dp[i]和count[i]，一般如果第一次出现更长最长子序列，count[i]==1，只有在小遍历第二次遇到该最长子序列时，才会累加count[i]+=count[j]，则关键实现代码如下：

for (int i = 0; i < size; ++i) // 求出前面i个dp[i]和count[i]的值
{dp[i] = 1;count[i] = 1;for (int j = 0; j < i; ++j) // 更新dp[i]和count[i]{if (nums[i] > nums[j]){if (dp[i] < dp[j] + 1){dp[i] = dp[j] + 1;count[i] = count[j];}else if (dp[i] == dp[j] + 1){count[i] += count[j];}}}// 根据已求得的dp[i]和count[i]，求出asn
}

`1.2.2根据已求得的`dp[i]和count[i]求出asn

根据前面已经更新的dp[i]和count[i]，求出最长子序列长度asn。即假如有新增最长子序列，则直接更新asn=count[i]，否则有相同最长子序列dp[i]==maxLen，则累加所有最长子序列长度asn+=count[i]。关键代码如下：

for (int i = 0; i < size; ++i) // 大遍历
{dp[i] = 1;count[i] = 1;for (int j = 0; j < i; ++j) // 小遍历，更新dp[i]和count[i]{// ......}if (dp[i] > maxLen) // 假如有新增最长子序列，则直接更新{maxLen = dp[i];asn = count[i];}else if (dp[i] == maxLen) // 否则有相等最长子序列，则累加所有相同子序列count[i]{asn += count[i];}
}

1.3完整代码

class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int asn=0, maxLen=1, size = nums.size();vector<int> dp(size, 0), count(size, 0);for(int i=0; i<size; ++i) // 大遍历{dp[i] = 1;count[i] = 1;for(int j=0; j<i; ++j) // 小遍历，更新dp[i]和count[i]{if(nums[i] > nums[j]) // 出现更新子序列{if(dp[i] < dp[j] + 1) // 更新最长子序列长度{dp[i] = dp[j] + 1;count[i] = count[j];}else if(dp[i] == dp[j] + 1) // 出现相同最长子序列长度，累加所有相同最长子序列{count[i] += count[j];}}}if(dp[i] > maxLen) // 更新完后找出最长子序列dp[i]，大于maxLen则更新，否则累加{maxLen = dp[i];asn = count[i];}else if(dp[i] == maxLen) // 遇到相同最长子序列，需要累加所有相同最长子序列{asn += count[i];}}return asn;}
};