最长递增子序列问题及应用

300. 最长递增子序列

请参考 【Leetcode】计算最长系列（动态规划） 中对 300. 最长递增子序列 的讲解。解题方法主要有两种：动态规划、贪心+二分查找。

面试题 17.08. 马戏团人塔

1.题目描述

leetcode链接：面试题 17.08. 马戏团人塔

2.思路分析

题目要求在2个维度上(即身高 + 体重)同时保持严格递增。

那么我们可以先将其中一个维度排好序，以保证在一个维度上保持递增（此时并非严格递增）；之后就可以专注于处理另一个维度。

先对身高体重排序，身高升序排列，身高相同，体重降序排列，这里可以使用二维数组的lambda表达式写法。可以参考：Java数组、ArrayList、HashMap排序总结。

之后就是计算最长递增子序列。身高已经按升序了，只需要判断体重。处理体重的问题就是处理最长递增子序列的问题。

参考最长递增子序列的解法。

3.参考代码

方法一：动态规划（超时）

class Solution {public int bestSeqAtIndex(int[] height, int[] weight) {int n = height.length;int[][] person = new int[n][2];for (int i = 0; i < n; i++) {person[i] = new int[]{height[i], weight[i]};}// 身高相同，体重降序Arrays.sort(person, (o1, o2) -> o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0]);int[] dp = new int[n];Arrays.fill(dp, 1);int res = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < i; j++) {if (person[i][1] > person[j][1]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}res = Math.max(dp[i], res); }return res;}
}

方法二：贪心 + 二分查找

class Solution {public int bestSeqAtIndex(int[] height, int[] weight) {int n = height.length;int[][] person = new int[n][2];for (int i = 0; i < n; i++) {person[i] = new int[]{height[i], weight[i]};}// 身高相同，体重降序Arrays.sort(person, (o1, o2) -> o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0]);int[] dp = new int[n];Arrays.fill(dp, 1);int res = 0;for (int[] per : person) {int left = 0, right = res;while (left < right) {int mid = (right - left) / 2 + left;if (dp[mid] < per[1]) {  // 要找的是dp数组中第一个小于当前h的位置left = mid + 1;} else {right = mid;}}dp[left] = per[1];if (res == left) res++;}return res;}
}

二分查找可以直接调API：

通过二分法在已经排好序的数组中查找指定的元素，并返回该元素的下标。

1. 如果数组中存在该元素，则会返回该元素在数组中的下标
2. 如果数组中不存在该元素，则会返回 -(插入点 + 1)

int res1 = Arrays.binarySearch(int[] arr, int key);  // 默认搜索整个数组
int res2 = Arrays.binarySearch(int[] arr, int fromIndex, int toIndex, int key);  // 搜索数组指定索引内

class Solution {public int bestSeqAtIndex(int[] height, int[] weight) {int n = height.length;int[][] person = new int[n][2];for (int i = 0; i < n; i++) {person[i] = new int[]{height[i], weight[i]};}// 身高相同，体重降序Arrays.sort(person, (o1, o2) -> o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0]);int[] dp = new int[n];Arrays.fill(dp, 1);int res = 0;for (int[] per : person) {int i = Arrays.binarySearch(dp, 0, res, per[1]);if (i < 0) i = -(i + 1); // 如果没找到dp[i] = per[1];if (i == res) res++;}return res;}
}

354. 俄罗斯套娃信封问题

1.题目描述

leetcode链接：354. 俄罗斯套娃信封问题

2.思路分析

与上一题相同，只是身高体重的区间换成了信封的长宽，方法完全一样。

直接动态规划会超时，所以可以还是使用二分查找来优化。

3.参考代码

class Solution {public int maxEnvelopes(int[][] envelopes) {int n = envelopes.length;Arrays.sort(envelopes, (a, b) -> (a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]));int[] dp = new int[n];Arrays.fill(dp, 1); // 初始化为1，表示当前信封int max = 0;// 二分查找for (int[] env : envelopes) {int left = 0, right = max;while (left < right) {int mid = (right - left) / 2 + left;if (dp[mid] < env[1]) {  // 要找的是dp数组中第一个小于当前h的位置left = mid + 1;} else {right = mid;}}dp[left] = env[1];if (left == max) {max++;}}return max;}
}

面试题 08.13. 堆箱子

1.题目描述

leetcode链接：面试题 08.13. 堆箱子

2.思路分析

动态规划：

本题与上两题相似，都是多维度下的最长递增子序列问题。这道题是三维，宽度，深度，高度都要大于上面的箱子。

同样的先按照各维进行排序。然后动态规划，注意每一次的dp[i]初始化为 box[i][2];。

3.参考代码

class Solution {public int pileBox(int[][] box) {// 按宽度，深度，高度升序排列Arrays.sort(box, (a, b) -> (a[0] == b[0] ? (a[1] == b[1] ? a[2] - b[2] : a[1] - b[1]) : a[0] - b[0]));int[] dp = new int[box.length];int res = 0;for (int i = 0; i < box.length; i++) {dp[i] = box[i][2];for (int j = 0; j < i; j++) {if (box[j][0] < box[i][0] && box[j][1] < box[i][1] && box[j][2] < box[i][2]) {dp[i] = Math.max(dp[i], dp[j] + box[i][2]);}}res = Math.max(res, dp[i]);}return res;}
}

1691. 堆叠长方体的最大高度

1.题目描述

leetcode链接：1691. 堆叠长方体的最大高度

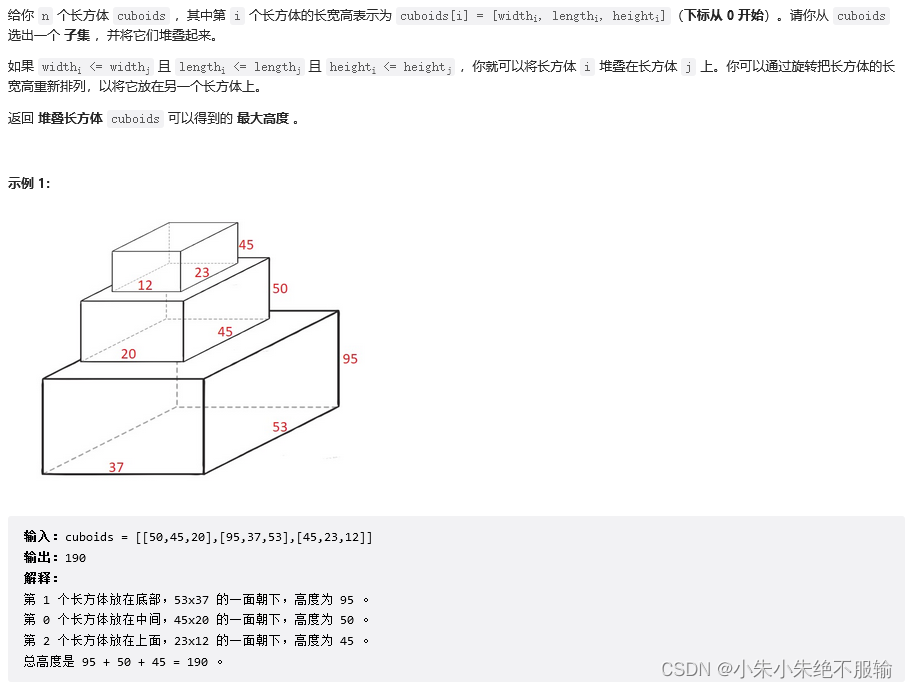
2.思路分析

与上一题一致，只是多了一步，开始的时候需要先对每个正方体内部进行排序，升序排序后，高度在最后的位置，其余与上一题完全相同。

3.参考代码

class Solution {public int maxHeight(int[][] cuboids) {for (int[] cuboid : cuboids) {Arrays.sort(cuboid);}Arrays.sort(cuboids, (a, b) -> (a[0] == b[0] ? (a[1] == b[1] ? a[2] - b[2] : a[1] - b[1]) : a[0] - b[0]));int[] dp = new int[cuboids.length];int res = 0;for (int i = 0; i < cuboids.length; i++) {dp[i] = cuboids[i][2];for (int j = 0; j < i; j++) {if (cuboids[i][0] >= cuboids[j][0] && cuboids[i][1] >= cuboids[j][1] && cuboids[i][2] >= cuboids[j][2]) {dp[i] = Math.max(dp[i], dp[j] + cuboids[i][2]);}}res = Math.max(dp[i], res);}return res;}
}

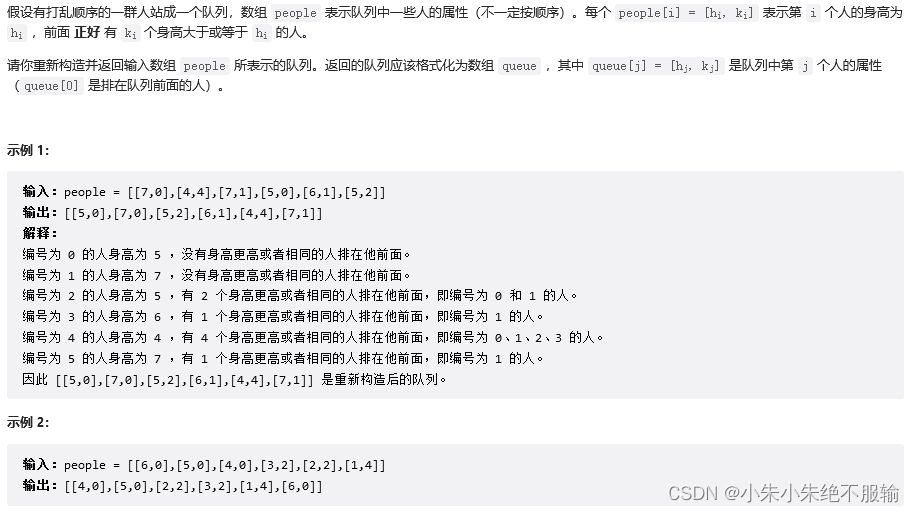
406. 根据身高重建队列

1.题目描述

leetcode链接：406. 根据身高重建队列

2.思路分析

先按身高降序排序，身高相同，再按k值升序排序。

之后顺序遍历将元插入结果集。就是小的反而后插入相对应的索引。

示例：

输入: [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
输出:
[[7, 0]]
[[7, 0], [7, 1]]
[[7, 0], [6, 1], [7, 1]]
[[5, 0], [7, 0], [6, 1], [7, 1]]
[[5, 0], [7, 0], [5, 2], [6, 1], [7, 1]]
[[5, 0], [7, 0], [5, 2], [6, 1], [4, 4], [7, 1]]

3.参考代码

class Solution {public int[][] reconstructQueue(int[][] people) {// 身高降序排，身高相同，k小的排前面Arrays.sort(people, (a, b) -> (a[0] == b[0] ? a[1] - b[1] : b[0] - a[0]));List<int[]> list = new LinkedList<>();for (int[] p : people) {list.add(p[1], p);}return list.toArray(new int[people.length][]);}
}